支配

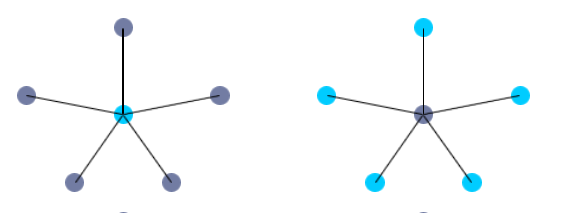
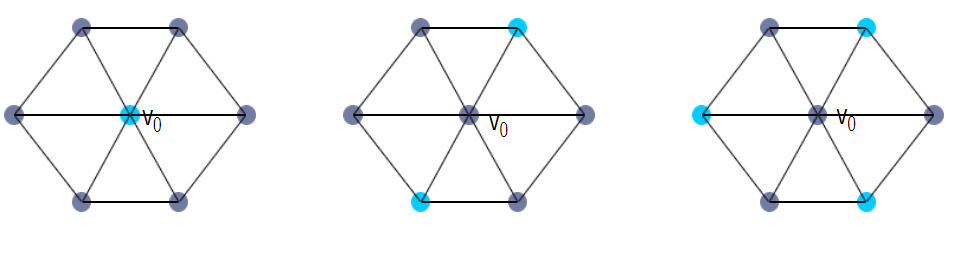
  • 支配集： 挑选出一些顶点组成支配集，使得所有其他的点都和这个集合中的点相连。
  • 极小支配集： 支配集删去任意顶点之后不是支配集
  • 最小支配集： 支配集中顶点数量最小的
  • 只配速： 最小支配集中点的个数

例如图中两个都是极小支配集，其中第一个是最小支配集。

定理： 无向图无孤立点，$V_1^$是极小支配集，则存在$V_2^$也是极小支配集，且$V_1^ \cap V_2^ = \oslash$

证明：

  1. $V_1^$是支配集，那么$V - V_1^$也是支配集
    反证： 如果不是支配集，那么存在$\exists u \in V_1^ , \forall v \in V - V_1^ , (u, v) \notin E$, 因为u不是孤立点，那么$V_1^ - {u}$还是支配集。所以$V - V_1^$是极小支配集
  2. $V - V_1^*$是支配集，那么它的子集中必定存在极小支配集

求最小支配集

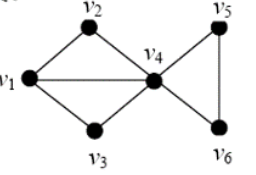
例如求上图的最小支配集

每一项的含义是该项是否在最小支配集中，例如$v_1$表示$v_1$是否在支配集中，如果在就为真。

这个式子每个括号中以$v_1 , v_2 …$开头，并且括号中的其他项就是和开头的那个有连接的项。

例如： $v_1$和$v_2 , v_3$有连接，因此他们三个在第一个括号中

每个括号中的含义可以表示为要么开头那项在支配集中，要么他可以被其他项支配（因为每个括号中其他项都和第一项有连接）。

因此这个等式如果为真就表示所有顶点都可以被支配。但是求这个式子还需要化简

(a + b)(a + c) = a + bc
a(a + b) = a//吸收率
根据上面两个式子就可以进行化简了

覆盖

点覆盖

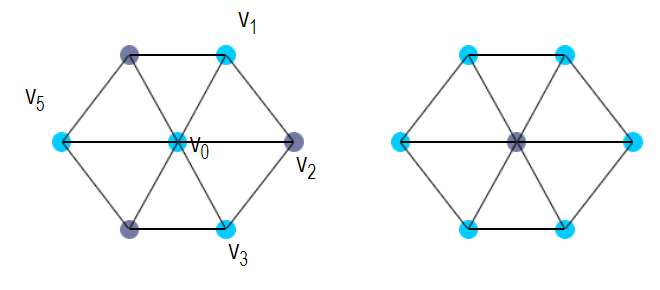
覆盖是选取一些点，它与所有边关联。

他也有极小点覆盖，最小点覆盖等概念。

例如图中都是极小点覆盖，其中第一个是最小点覆盖，点覆盖数是4

点覆盖一定是支配集，但是极小点覆盖不一定是极小支配集

求最小点覆盖集

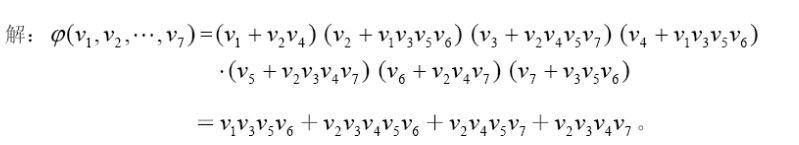
  • 意义： 我们可以把括号中第一个点称为覆盖点（随便说的名字），每个括号的含义是覆盖点在覆盖集中或它可以被其他点覆盖。注意这里是乘而不是加，因为所有其他点合起来才可以覆盖覆盖点的每一条边。这个式子为真则表示存在一个覆盖集
  • 化简： 可以看到每一个括号中只有两项，所以直接乘开即可。

边覆盖

边覆盖是选取一个边的子集使得任意一个点都可以和子集中的边相连。

独立集

独立集是一个顶点的子集，子集中的任意两个点都没有边相连。

和前面不同独立集是点越多越难找，因此存在最大独立集和极大独立集

  • 极大独立集： $V^*$是独立集，但是任意再加一个点都不是独立集
  • 最大独立集： 独立集中点数目最多的。

定理：无向图无孤立点，$V^*$是极大独立集，那么他也是极小支配集

证明：

  1. $V^$是极大独立集，那么它一定是支配集
    反证： 如果他不是支配集，也就表示有点和集合中的任意一点都不相连，那么把这一点添加到集合中还是独立集，与$V^    $是极大独立集矛盾
  2. $V^$是极小支配集
    反证： 如果它不是极小支配集，那么存在$V^     - {u}$也是支配集，那么存在$v \in V^ - {u}$，(u, v)中存在一条边相连，和$V^$是独立集相矛盾

但是它的逆命题不一定成立，极小支配集不一定是极大独立集。

定理： 无向图无孤立点， 如果一个集合是点覆盖，那么它的补集是独立集。

证明： 如果它的补集不是独立集，也就表示补集中有边相连，那么原集合就没有覆盖到这条边，与该集合是点覆盖相矛盾。

这条定理的逆命题也成立。根据这条定理，可以把求极大独立集的问题变成求极小点覆盖的问题。

团

团是图中的完全子图，也就是所有点都相互连接。

  • 极大团： 再加一个点就不是团
  • 最大团： 点数最多的团

定理： 无向图$V$是图G的团 $\Longleftrightarrow$ $V$是G的补集的独立集

推论： 如果是最(极)大团，对应着最(极)独立集

匹配

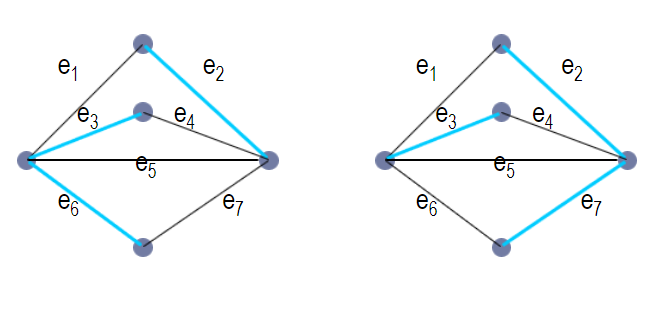
匹配是边的集合，并且集合中任意两条边都不相邻（顶点不重合）

他也是匹配数量越多越困难，因此存在极大匹配和最大匹配。

  • 饱和点： v是M（M是一个匹配集）中的边的顶点
  • 不饱和点：…
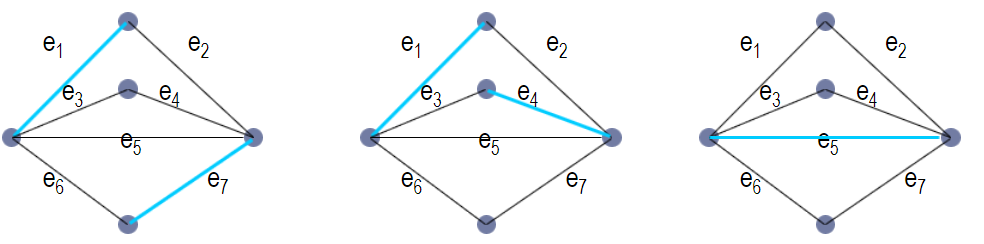
  • 交错路径： 在M和E-M中交替取边的路径。例如上面$e_3 , e_4 , e_2$是一个交错路径
  • 可增广交错路径： 两端都是非饱和点的交错路径
  • 完美匹配： 没有非饱和点的匹配

求解最大匹配：

  • 从一个匹配开始
  • 逐一检查非饱和点，对每一个不饱和点寻找增广路径
  • 得到更大匹配
  • 递归直到没有不饱和点或增广路径

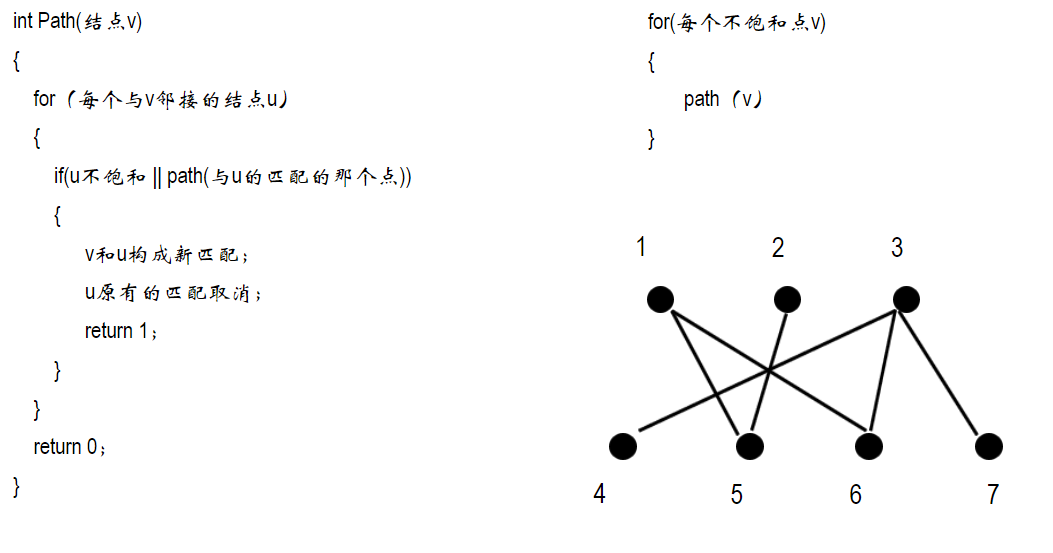
上面是求解二部图匹配的一种算法。关键在于if语句中的判断条件。看看对面是否已经匹配或者和对面匹配的人能否换个位置。

以图中的二部图为例：

  • 首先是1进行选择，它选择了5并且将1和5的饱和置1.
  • 然后轮到2进行选择，2发现5已经饱和了，与他它想让5匹配的点挪个位置和别人组队，这样他就可以和5进行组队了。
  • 和5组队的是1,1再运行path发现还可以和6组队，于是他和6组队并且清除原来的标记，然后2和5组队，结束。
  • 之后是3进行选择，3直接选择4匹配结束。