A*搜索与博弈树

本文最后更新于 2024年10月1日 上午

8数码问题

8数码问题是在一个九宫格上有8个数，初始中间一个空缺，外围随机排布，最终要8个数按顺序排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
初始
328
1 4
567

中间的格子可以利用，也就是说可以
328
 14
567

最终
123
8 4
765

可以使用广度优先搜索进行遍历，那么第一层有四种情况（将上下左右4个移动到中间)，然后第二层有8种
1
2
3
4
5
6
7
8
9
10
11
12
13
第二层的一个例子
328
 14
567

第一种
 28
314
567
或者
328
514
 67

然后就这样不断遍历，直到找到最终结果

但是这样的复杂度明显太高，我们可以定义一个函数预先判断走那条路可能得到更好的结果。

定义f(n) = g(n) + h(n).

其中g(n)表示现在是第几层的搜索，h(n)表示现在和最终结果还有多少不同

拿上面的例子

1
2
3
4
5
6
7
8
9
10
11
假设现在到了
 28
314
567
则g(n) = 2

他和最终结果
123
8 4
765
有2个相同，因此h(n) = 6

然后根据上面的这个式子，每次选取最小的进行搜索，这样相比于盲目的搜索更快

A*算法

通过上面的例子，我们对A算法有了初步的了解。A算法的关键就是定义

  • g(n): 表示当前已经花费的代价。也可以说是距起点的代价
  • h(n): 预计到终点所需要花费的代价。也就是启发函数

求解的关键就是寻找一个合适的h(n),假设从该点到终点的真实代价为r(n)

  • h(n)始终小于r(n): 表示我们一定可以找到一条最小路径，但是如果h(n)小的越多，所遍历的点就越多，速度也就越慢
  • h(n) > r(n): 速度很快，但是不保证可以到达终点
  • h(n) = r(n): 将找到最佳路径并且速度很快

图中h(n)的选择

曼哈顿距离

h(n) = dis = |$x_1 - x_2$ | + |$y_1 - y_2$|

对角线距离

允许斜着走的时候可以考虑对角线距离.也就是允许从(0, 0)直接走到(1, 1)

1
2
3
4
5
6
7
8
假设走一格的代价为D， 从对角线走代价为D2
一般可以让D2 = sqrt(2) * D(对角线是根号2)

double delta_x = abs(x1 - x2);
double delta_y = abs(y1 - y2);
double ans = (delta_x + delta_y) * D + (D2 - 2 * D) * min(dx, dy)

这个式子后面的含义是减去走对角线更快的那部分。因为D2 - 2 * D一般是负数

欧几里得距离

两点之间距离公式,上下也可以移动的时候可以试试这个

博弈树

博弈理论基础

博弈有三个要素：博弈的参与人员、策略集和收益。博弈的目标就是为了获得尽可能多的收益。当然收益并不是指狭隘的输赢，存在双输和双赢的情况。

博弈的假设有三点，满足三点才可以进行下面的推导

  1. 理性人： 博弈者足够聪明，可以选择对自己最有利的判断并执行
  2. 规则透明： 相互了解对方的策略集（例如打牌就不是，你不知道对方的牌就不知道对方接下来会怎么出牌）
  3. 自我利益最大化

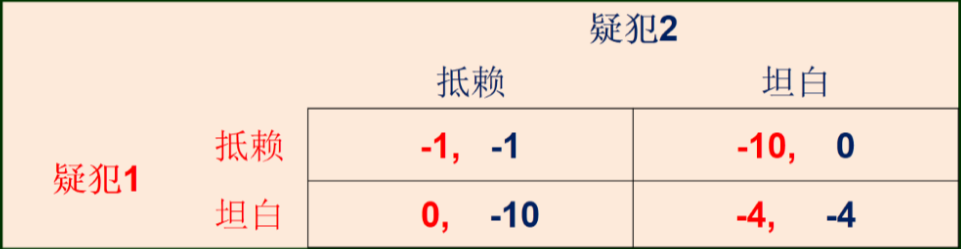
博弈的一个典型例子“囚徒困境”

警察抓到了两个嫌疑犯，但是没有证据，现在需要诱供。他对两个嫌疑犯说，如果两个人都抵赖，那么没有证据抓你们，但是我可以找一个由头给你们判一年。如果你坦白他抵赖，那么他判十年你释放。如果两个人都坦白，那么只需要判四年。

如上图如果a坦白，b抵赖，那么a获得好处比抵赖更多，如果b坦白，a也坦白获得的价值比抵赖更多。现在就很简单了，无论b如何选择，a选择坦白都可以获得更好的结果。于是两人都会这样选择，最后两个人都会坦白。

从直观上理解，两个人都抵赖最终可能结果会更好，但是基于完全理性人的假设却让他们避开了这个结果，最终获得双输的局面。

这其实是规则设计者精心设计的，警察想尽办法让选择坦白更为有利。此外还有旁观者（学者）视角和当事人视角进行观察。从当事人视角，选择坦白更为有利，从旁观者视角，选择抵赖更为有利。

博弈的求解

博弈最终就是要寻求均衡，也就是博弈参与人都不想改变当前情况。可以使用收益矩阵进行刻画并求得均衡情况。

  • 严格占优策略： 无论你如何选择，我这样选择总是最优
  • 严格最佳应对： 如果你这样做，我这样做才可以收益最大。

如果双方都有严格占优策略那么毫无疑问均衡情况就是两个都选严格占优策略的情况。

如果一方有严格占优策略那么该方必定会选严格占优策略，那么另一方也必定会选择严格最佳应对，那么此时也可以达到均衡。

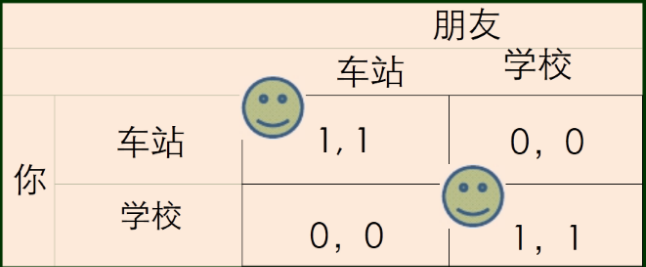
但是有时候比一定有严格占优策略。例如，两个人去约会结果迷路了，他们实现指定了学校门口和车站两个地点进行集合，则此时收益矩阵为

这个时候我们就需要使用均衡的定义去判断均衡情况了。如果两个人都在车站或门口显然他们不想改变当前状况。如果一个在车站一个在门口那么无疑任何一个人移动位置可以得到更高的收益，于是他们此时还想变更选择，因此不是均衡情况。

可以得知上迷昂有两个均衡情况。并且可能会选择哪个是随机的。但是至少我们可以缩减选择的范围。

博弈树

例： 一字棋问题

设有一个3行3列的棋盘,如图4.5所示。两个棋手轮流走每个棋手走步时往空格上摆一个自己的棋子,谁先使自己的棋子成三子一线为赢。设MAX方的棋子用×标记。MIN方的棋子用O标记,并规定MIN方先走步。

MAX是要让结果朝有利于自己的方向发展，因此他会选评估函数最大的值，而MIN会选最小的值

定义评估函数为：

  • 若P是MAX的必胜局，则e(P) = +$\infty$
  • 若P是MIN的必胜局， 则e(P) = -$\infty$
  • 否则，e(P) = e(+P) - e(-P).其中e(+P)是棋局上可能使x成三子的数目，e(-P)是可能使O成三子的数目。

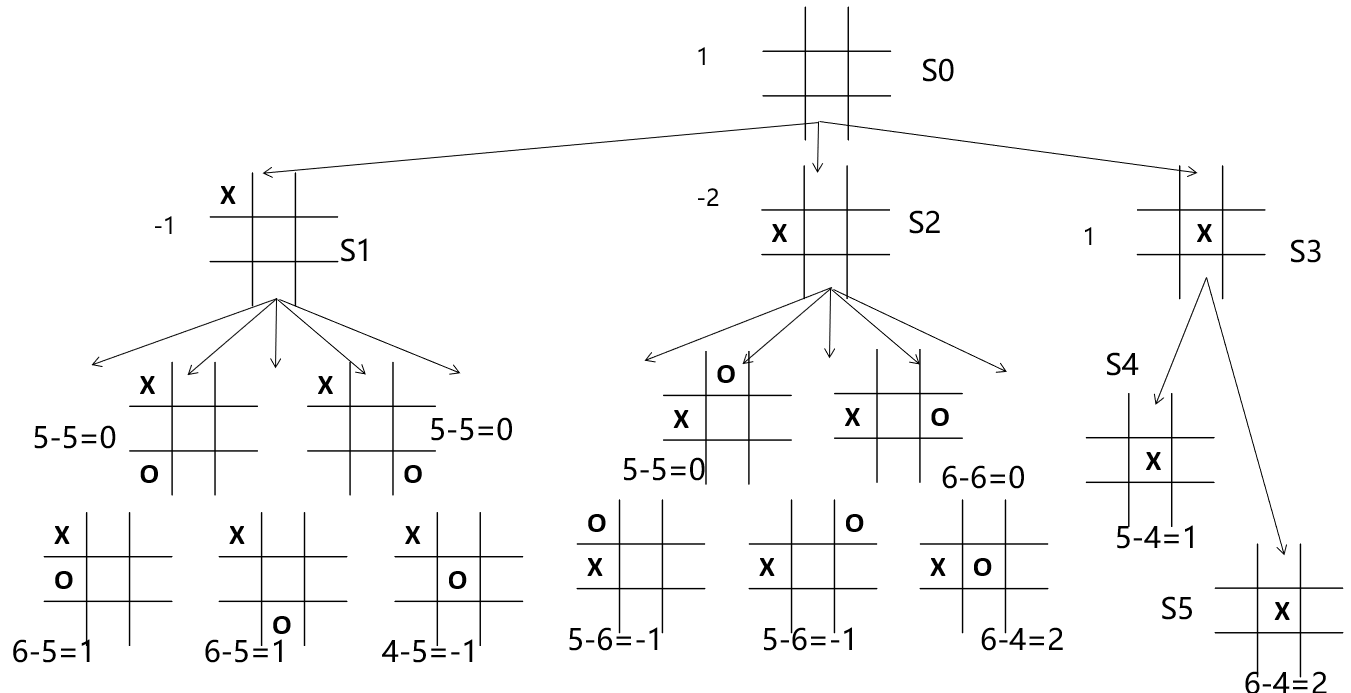
例如上图中e(P) = 9 - 4 = 5

它的生成树为

这种直接展开状态空间树显然太大，因此需要使用一定的剪枝技术。

$\boldsymbol{\alpha - \beta 剪枝}$

  • $\alpha$剪枝： 任何MIN节点的$\beta$值小于等于先辈节点(MAX节点)的$\alpha$值，则该节点可以停止继续展开。因为MIN节点是要找小的，而MAX是要找大的，现在MIN节点已经小到MAX一定不会选了，MIN继续展开也只可能越来越小，因此无需展开
  • $\beta$剪枝： 任何MAX节点的$\alpha$值大于等于先辈节点的$\beta$值，则该节点可以停止展开。

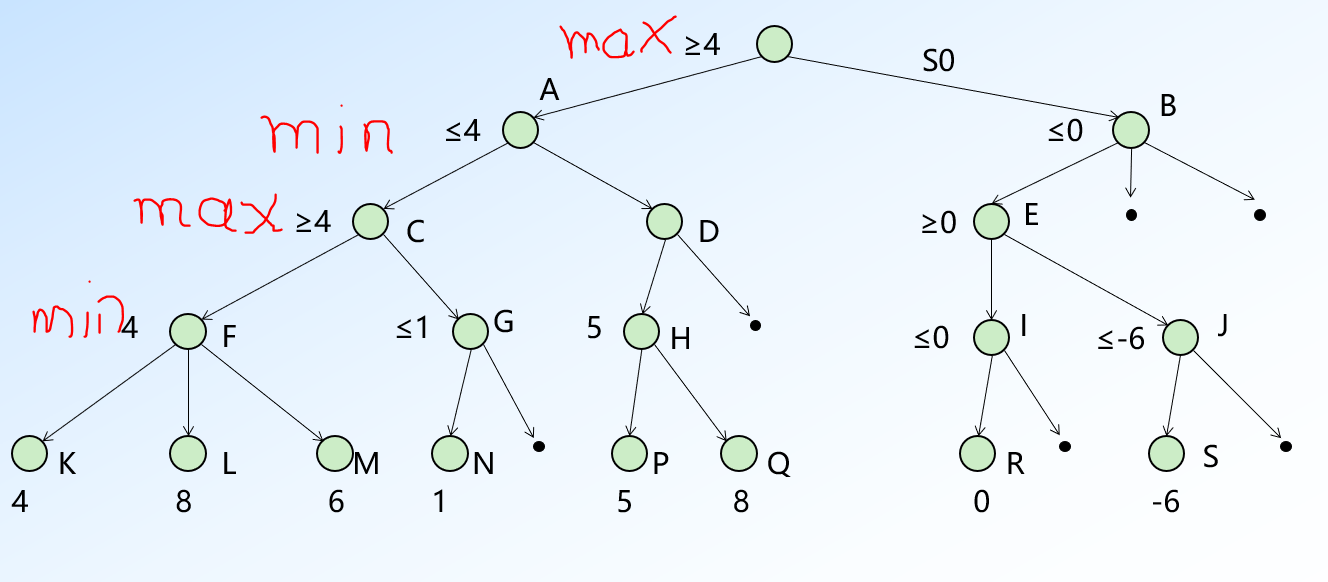
例：

  1. 深度优先搜索找到k的值是4，然后向上到f再向下找到l的值是8，同理m的值是6。然后F是min节点，因此它的值是4
  2. 然后f节点向上，c节点得知f节点的值，现在c节点需要>4的值才会更新。然后c向下到g再到n。n往上更新g为1，现在由于g小于c现在的值4，再继续找g也只会比1更小，但是c一定不会选用，没有意义，因此停止更新g。
  3. a的值暂时为4并且他现在要比4小才会更新。然后D的值经过更新之后为5，由于D只会越来越大而A现在需要找比4小的，因此更新D没有意义，停止更新。

井字棋问题求解代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
#include<iostream>
#define player 1
#define ai 0
#define UNCONFIRM 10000
using namespace std;
char board[3][3];
char player_side, ai_side;
void print_board()
{
    for(int i=0; i<3; i++)
    {
        for(int k=0; k<3; k++)
        {
            cout << board[i][k] << " ";
        }
        cout << endl;
    }
}

int check()
{
    int ans[8];
    for(int i=0; i<8; i++)
    {
        if(i < 3)
            ans[i] = board[i][0];
        else if(i < 6)
            ans[i] = board[0][i -  3];
        else if(i == 6)
            ans[i] = board[0][0];
        else
            ans[i] = board[0][2];
    }
    for(int i=1; i<3; i++)
    {
        for(int k=0 ;k<8; k++)
        {
            if(k < 3)
            {
                if(ans[k] != board[k][i])
                    ans[k] = -1;
            }
            else if(k < 6)
            {
                if(ans[k] != board[i][k-3])
                    ans[k] = -1;
            }
            else if(k == 6)
            {
                if(ans[k] != board[i][i])
                    ans[k] = -1;
            }
            else
            {
                if(ans[k] != board[i][2-i])
                    ans[k] = -1;
            }
        }
    }

    for(int i=0; i<8; i++)
    {
        if(ans[i] == 'x')
        {
            return 'x';
        }
        else if(ans[i] == 'o')
        {
            return 'o';
        }
    }
    for(int i=0; i<3; i++)
    {
        for(int k=0; k<3; k++)
        {
            if(board[i][k] == '.')
            {
                return 0;
            }
        }
    }
    return 3;
}

int prune(int owner, int parent_score)
{
    int m_score = UNCONFIRM;
    int ans = check();
    if(ans == ai_side)
    {
        return -60;
    }
    else if(ans == player_side)
    {
        return 60;
    }
    else if(ans == 3)
    {
        return 0;
    }

    for(int i=0; i<3; i++)
    {
        for(int k=0; k<3; k++)
        {
            if(board[i][k] == '.')
            {
                board[i][k] = owner == player ? player_side : ai_side;
                int temp = prune(!owner, m_score);
                if(m_score == UNCONFIRM)
                {
                    m_score = temp;
                }
                else
                {
                    if(owner && temp > m_score)
                    {
                        m_score = temp;
                        if(m_score > parent_score && parent_score != UNCONFIRM)
                        {
                            board[i][k] = '.';
                            return m_score;
                        }
                    }
                    if(!owner && temp < m_score)
                    {
                        m_score = temp;
                        if(m_score < parent_score && parent_score != UNCONFIRM)
                        {
                            board[i][k] = '.';
                            return m_score;
                        }
                    }
                }
                board[i][k] = '.';
            }
        }
    }
    return m_score;
}

void round(int owner)
{
    if(owner == player)
    {
        print_board();
        cout << "你的回合，请输入位置(x, y)[起点为(0, 0)]: ";
        int x=0,y=0;
        cin >> x >> y;

        while(x < 0 || x >=3 || y < 0 || y >= 3 || board[x][y] != '.')
        {
            cout << endl <<"输入错误，请重新输入: ";
            cin >> x >> y;
        }
        board[x][y] = player_side;
    }
    else
    {
        int m_score = UNCONFIRM;
        int loc_x=0, loc_y=0;
        for(int i=0; i<3; i++)
        {
            for(int k=0; k<3; k++)
            {
                if(board[i][k] == '.')
                {
                    board[i][k] = ai_side;
                    int temp = prune(!owner, m_score);

                    if(temp < m_score)
                    {
                        m_score = temp;
                        loc_x = i;
                        loc_y = k;
                    }
                    board[i][k] = '.';
                }
            }
        }

        board[loc_x][loc_y] = ai_side;
    }
}

int main()
{
    for(int i=0; i<3; i++)
    {
        for(int k=0; k<3; k++)
        {
            board[i][k] = '.';
        }
    }
    cout <<"你想先下吗(y/n)"<<endl;
    char is_first;
    cin >> is_first;
    int beginner = 0;
    if(is_first == 'y')
    {
        player_side = 'x';
        ai_side = 'o';
        beginner = 1;
    }
    else if(is_first == 'n')
    {
        player_side = 'o';
        ai_side = 'x';
    }
    else
    {
        cout << "输入错误，结束" << endl;
        return 0;
    }
    int check_sum = 0;
    while((check_sum = check()) == 0)
    {
        round(beginner);
        beginner = !beginner;
    }

    if(check_sum == ai_side)
    {
        cout << "ai win" << endl;
    }
    else if(check_sum == player_side)
    {
        cout << "player win" << endl;
    }
    else
    {
        cout <<"平局"<<endl;
    }
}

算法
A*搜索与博弈树
https://www.xinhecuican.tech/post/19899506.html
作者
星河璀璨
发布于
2021年5月7日
许可协议