红黑树

性质

红黑树是一颗二叉搜索树，并且在每个节点上增加一个变量来储存颜色，可以是红或者是黑。红黑树保证了没有一条路径会比其他路径长两倍。

每个节点有五个属性：color、key、left、right、p(parent)。

红黑树满足以下性质：

• 根节点是黑色
• 每个叶结点是黑色的。
• 如果一个节点是红色，则两个子节点是黑色
• 对于每个节点，从这个节点到所有后代节点的简单路径上，均包含相同数目的黑色节点。

在叶结点中不存在值，可以用一个哨兵节点来代指叶结点。哨兵节点颜色为黑，其他值任意，之后一旦到叶结点就连接到哨兵，这样可以减少空间占用。

从某一节点出发（不包含这个节点）的任意一条简单路径上黑色节点的个数叫这个点的黑高。定义红黑树的黑高是根节点的黑高。

可以证明，节点数为n的红黑树高度至多为2lg(n+1).

旋转

插入和删除可能会改变红黑树的性质，这个时候就需要通过旋转来恢复红黑树的性质。

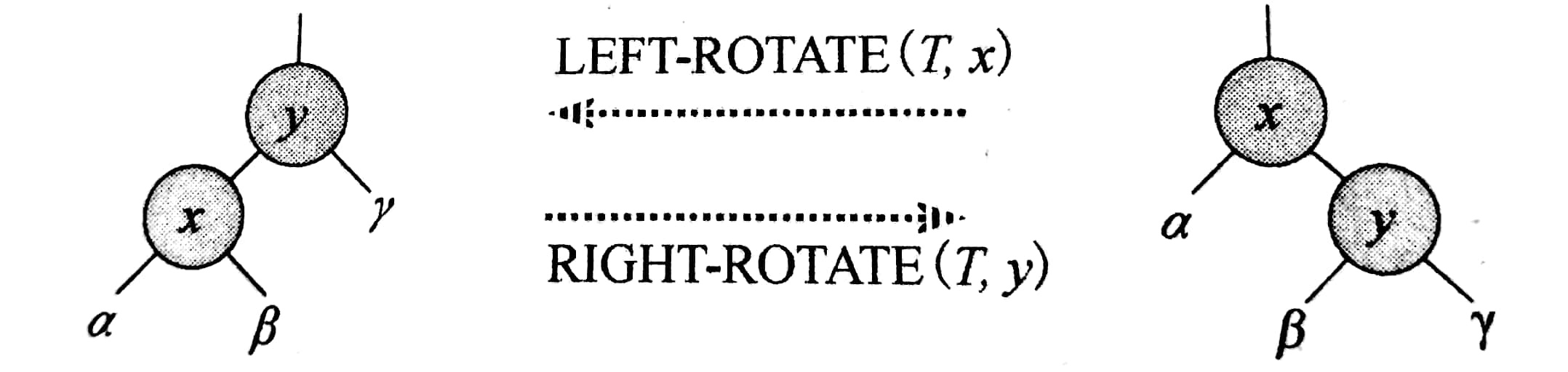
左旋的过程是把y的左边给x，然后x变为y的左儿子。右旋可以类比。

注意： 旋转之后性质不改变并且旋转的两个节点颜色可以互换。

左旋函数：

void left_rotate(node* t, node* x)
{
    //t是根节点
    node* y = x->right;
    x->right = y->left;
    if(y->left != NULL)//设置y->left的父辈节点
    {
        y->left->p = x;
    }
    y->p = x->p;//设置y的父辈节点
    if(x->p == NULL)//如果x->p为NULL，说明它是根节点
    {
        t->root = y;
    }
    else if(x == x->p->left)//这是设置原来x的父辈的连接
    {
        x->p->left = y;
    }
    else
    {
        x->p->right == y
    }
    y->left = x;
    x->p = y;
}

插入

我们可以先找到插入位置（用二叉搜索树的方法），然后将这个点着色为红。为了保证性质，我们还要用一个函数对节点重新着色并旋转。

调整函数：

void fixup(node* t, node* x)
{
    while(x->p->color == red)
    {
        if(x->p == x->p->p->left)
        {
            node* y = x->p->p->right;
            if(y->color == red)//情况1
            {
                x->p->color = black;
                y->color = black;
                x->p->p->color = red;
                x = x->p->p;
            }
            else if(x == x->p->right)//情况2
            {
                x = x->p;
                left_rotate(t, x);
            }
            x->p->color = black;//情况3
            x->p->p->color = red;
            right_rotate(t, x->p->p);
            
        }
        else
        {
            //和上面一样，就是把左右换一下
        }
        
    }
    t->root->color = black;
}

因为插入的是红色的节点，所以所有路径黑色节点数目相同这个性质不可能破坏。

这里可能被破坏的是根节点必须是黑色和红节点儿子必须是黑色两个性质。所以要从这两个性质着手去解决。

上面这个函数每次while都要保持下面性质：

• x是红节点
• 如果x->p是根节点，那么x->p是黑节点
• 如果性质被破坏，只可能是上面两条。如果是第一条，那么x是根节点并且是红节点，如果是第二条，那么它是红并且它的父亲是红。

上面三种情况区别是叔节点颜色不同。在所有情况中，相同的地方是x->p->p一定是黑色，因为x->p一定是红色。

情况1：叔节点是红色

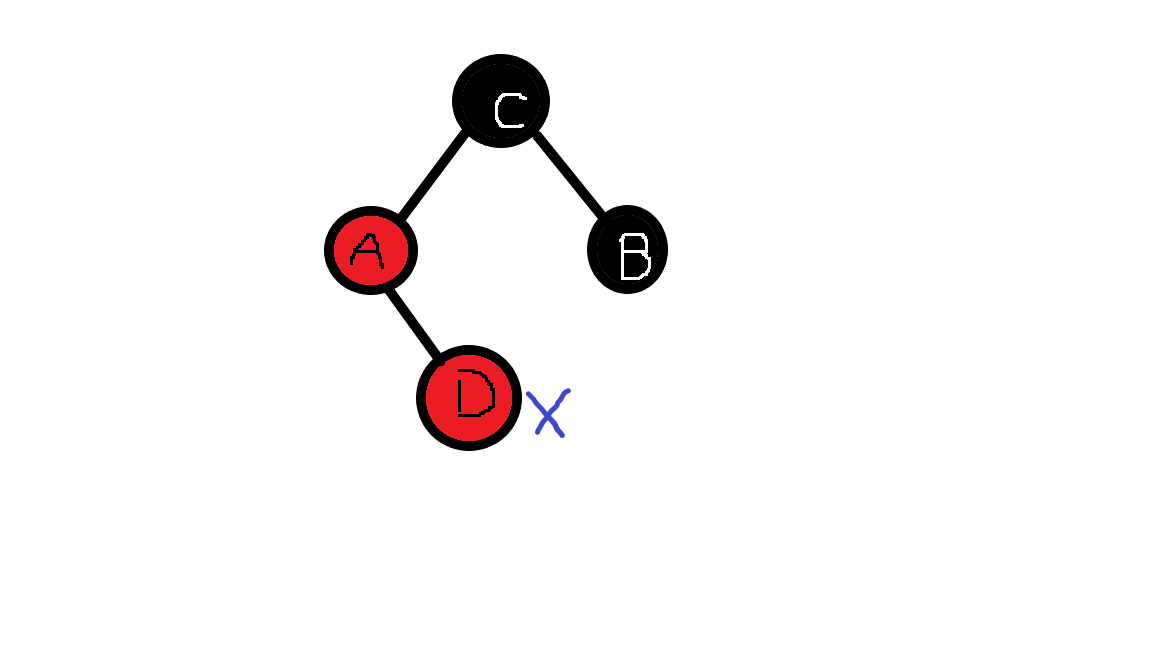
如图，左边是最开始的情况，白色代表红色。我们就可以把A和D图成黑色，然后C变成红色，这样每条路径黑色节点数目仍没变，但是此时C变成了红节点，可能和C的父亲有冲突，所以我们要把指针移动到C点

情况2，情况3： 叔节点是黑色并且x是左孩子/右孩子

情况2是x为右孩子。

情况2可以通过一个左旋变成情况3，此时x是左孩子。

此时把D和A都是红色。再让C一个右旋就让D到了上面（开始进行了一次左旋D到了A上面）然后让D为黑色，A和C为红色就可以了。并且这个时候循环也会结束，因为

删除

首先要基于基础的搜索二叉树删除操作，即如果删除节点是叶结点，直接删除，如果删除节点只有一个子节点，那么删除这个节点后还要让它的父节点连接这个节点的子节点，如果有两个子节点，那么要让它的前驱（或后继）来替代他。并且它的前驱的右子节点连接它的父节点。

总的函数过程为：

transplant(node* t, node* u, node* v)//删u节点操作，用v替代
{
    if(u->p == NULL)
    {
        t->root = v;
    }
    else if(u == u->p->left)
    {
        u->p->left = v;
    }
    else
    {
        u->p->right = v;
    }
    v->p = u->p;
}

fixup(node* t, node* x)
{
    while(x != t->root && x->color == black)
    {
        if(x == x->p->left)
        {
            node* w = x->p->right;
            if(w->color == red)//情况1
            {
                w->color = black;
                x->p->color = red;
                left_rotate(t, x->p);
                w = x->p->right;
            }
            if(w->left->color == black && w->right->color == black)
            {
                w->color = red;//情况2
                x = x->p;
            }
            else if(w->right->color == black)//情况3
            {
                w->left->color = black;
                w->color = red;
                right_rotate(t, w);
                w = w->p->right;
            }
            w->color = x->p->color;//情况4
            x->p->color = black;
            w->right->color = black;
            left_rotate(t, x->p);
            x = t->root;
        }
        else
        {
            //就是左右交换一下
        }
    x->color = black;
}

            
        
delete(node* t, node* x)
{
    //y->original->color保存的是y发生改变之前的颜色
    node* z;
    node *y = x;
    y->original->color = y->color;
    if(x->left == NULL)
    {
        z = x->left;
        transplant(t, x, x->right);
    }
    else if(x->right == NULL)
    {
        z = x->right;
        transplant(t, x, x->left);
    }
    else//如果两个子树都不为空
    {
        y = minimum(x->right);//找到x的后继
        y->original->color = y->color;
        z = y->right;
        if(y->p == x)
        {
            z->p = y;
        }
        else
        {
            transplant(t, y, y->right);
            y->right = x->right;
            y->right->p = y;
        }
        transplant(t, x, y);
        y->left = x->left;
        y->color = x->color;
    }
    if(y->original->color == black)
    {
        fixup(t, z);
    }
}

保持y是要被删除的元素,因此如果y最初的颜色是黑色就可能改变性质。而z保存的是y的原始位置。

在fixup中，while循环总目标是把额外的黑色沿着树往上提。

while节点退出条件：

• x指向红黑节点（两种颜色）。然后再最后再将颜色变成单独的颜色。
• x指向根节点
• 执行适当的旋转和重新着色，退出循环。

在循环中，x总是指向双重黑色节点（双重黑色就是假设z位置处额外有一个黑色，之后y删除会移走一个黑色然后性质就符合了，但是多了一个黑色会导致开开始路径黑色数目就不同，所以要把这个双重黑色的节点放到根节点处，这样就不会有影响了，红黑色就是z处原来是红色。另外这是为了理解说的，和书上的不同）。

如果x是双重黑色，那么w（x的兄弟）不可能是NULL，因为这会导致两边黑色不相等。

情况1： x的兄弟w是红色的

它的目的是把兄弟节点变成黑色。先把父亲节点和兄弟节点的颜色设置好，然后进行旋转。会把情况变成情况2或3

情况2： w黑色，并且w的两个子节点是黑色

这个时候可以从w上去除一层黑色，也就是x变成单黑然后w变成红色，然后x到父亲节点（一定是红色），也就是说这个时候去掉了黑色但是性质不满足了（有两个红色），所以跳出循环后还要加一个把x变成黑色

情况3： w黑色，w左孩子红色，右孩子黑色

通过这种变换，会把情况变成情况4.

情况4： w黑色，w右孩子红色

这种情况也是可以去掉黑色的。然后把x设置成根是为了退出循环。