首先要了解红黑树.

顺序统计树指示在普通的红黑树上附加了一个参量，x->size。这个参量表示的是该节点的子树含有元素个数。

为了找出第i小的关键字，可以用：

select(node* x, int i)
{
    int r = x->left->size + 1;
    
    //x的序号，因为红黑树也是一个排序树，所以x一定比左边元素都大
    if(i == r)
    {
        return x;
    }
    else if(i < r)
    {
        return select(x->left, i);
    }
    else
    {
        return select(x->right, i-r);
    }
}

确定一个元素的秩

秩指的是排第几号元素。

rank(node* t, node* x)
{
    int r = x->left->size + 1;
    node* y = x;
    while(y != t->root)
    {
        if(y == y->p->right)//如果是右子树，那么还要加上左子树的数目
        {
            r = r+y->p->left + 1;
        }
        y = y->p;
    }
    return r;
}

我们知道，使用中序遍历可以得到排序树的排序。中间循环的过程就是找到x在父亲节点子树中位置然后再到祖宗节点中所处位置最后到根节点所处位置。

维护

对于插入，红黑树插入分为两个阶段，第一阶段是找位置，只需要沿途让size+1就好了，第二阶段是旋转。对于左子树， x是原来最上面的节点，现在size是x->left->size + x->right->size + 1， 对于右儿子y来说，y的size就是最开始x的size（因为现在它使根节点）

区间树

区间树是另一种红黑树的扩展。它和普通红黑树的区别是多了一个区间x->int(interval)表示，区间最大值是int.high(区间的右端点),最小值是int.low.

此外，还附加了max（以x为根的子树中所有区间端点的最大值）

x->max = max(x->int->high, x->left->max, x->right->max)

search(node* t, int(interval) i)//查找与i重叠的区间
{
    node* x = t->root;
    while(x != NULL && (x->int->low>i->high || x->int->high<i->low))//x!=NULL && i不在x的区间范围内
    {
        
        if(x->left != NULL && x->left->max >= i->low)
        {
            x = x->left;
        }
        else
        {
            x = x->right;
        }
    }
    return x;
}

最优二叉搜索树

给一个n个不同关键字的已排序序列，用这些关键字构建一个二叉搜索树。对于每个关键字ki，都有一个概率pi表示搜索概率。因为还有可能没有搜索到，所以还有n+1个伪关键字。

可以证明，最优二叉搜索树的子树也是最优二叉树。

所以我们求解的子问题为： 求解ki到kj的最优二叉搜索树。并且 j>=i-1.当j=i-1时，不包含关键字。

当j=i-1时，子树中只包含伪关键字di-1， 所以搜索代价是qi-1

当j>=i时，我们要选取一个根节点kr, ki到kr-1为左子树，kr+1到j为右子树。当一棵树成为另一棵树的子树时，因为每个节点的深度都加1，所以搜索代价的增加值应该是所有概率之和，记这个概率为w(i, j)

注意w(i, j) = w(i, r-1) + pr + w(r+1, j)

所以现在概率应该是原来左子树代价+原来右子树代价+增加代价

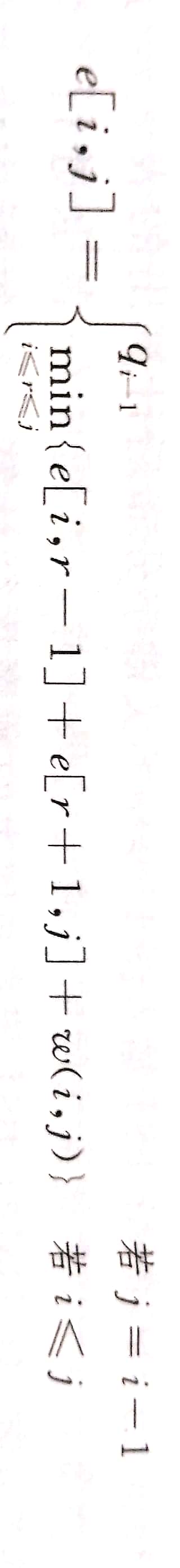
这就是最优搜索代价的递归公式。e[i, j]表示从i到j构成的二叉树的最优搜索代价。

bst(int* p, int* q, int n)
{
    //q是伪关键字搜索频率
    int max = 2147483647;
    int e[n+2][n+1], w[n+2][n+1], root[n+1][n+1];
    for(int i=1; i<=n+1; i++)
    {
        e[i][i-1] = q[i-1];
        w[i][i-1] = q[i-1];
        for(int l=1; l<=n; l++)
        {
            int j = i + l - 1;
            e[i][j] = max;
            w[i][j] = e[i][j-1] + p[j] + q[j];
            for(int r=i; r<=j; r++)
            {
                t = e[i][r-1] + e[r+1][j] + w[[i][j];
                if(t < e[i][j])
                {
                    e[i][j] = t;
                    root[i][j] = r;
                }
            }
        }
    }
    return e;
}