有限自动机
本文最后更新于 2024年10月1日 上午
基础概念
- 集合: 一群无序对象
- 序列(sequence): 以某种顺序排布的有序列表
- 元组(tuple): 有限序列称为元组
- 字母表: 字母表是任何非空有限集合,例如{a, b, c}
- 字符串: 字符串是在字母表中的字符组成成的有限序列,如abcac
语言: 字典序的一组字符串。例如{0, 1}组成的一个语言为{0, 1, 01, 10, 11, 000}.也就是说1比0更大,先比较长度,长度相同从高位向低位比较
语言的拼接: 定义两个语言L1, L2, 他们的拼接L1L2 = {xy | $x \in L_1, y \in L_2$}。类似于分配率
设L1 = {ab, ba, bb} L2 = {00, 11}, L1L2 = {ab00, ab11, ba00, ba11, bb00, bb11}
语言的闭包:
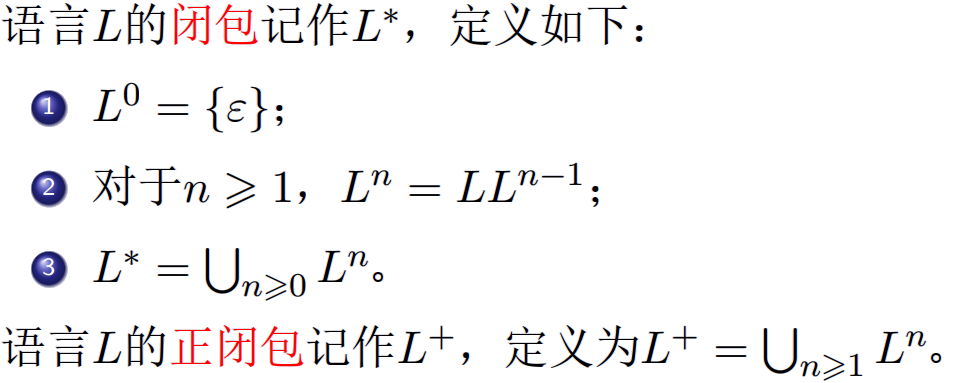
$L^* = L^+ \cup {\xi}$
例如, $\sum = {0, 1}$ L = {01, 10} $L^0 = {\xi}, L^1 = L = {01, 10}, L^2 = L * L = {0101, 0110, 1001, 1010} …$
$L^* = {\xi , 01, 10, 0101, 0110, 1001, 1010, 010101, 010110…}$
有限自动机
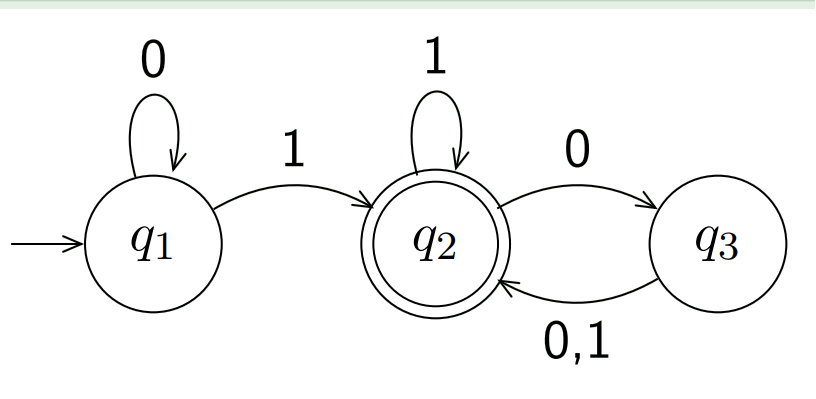
如图所示为一个有限状态自动机,q2是接收状态。跳转到接受状态就表示当前输入可行。
该自动机的含义为存在1并且后面接着偶数个0为结尾。例如10100,1011都是可接受的输入
定义:
有限自动机是一个五元组(Q, $\sum$, $\delta$, $q_0$, F)
- Q: 状态集合,例如上面的{q1, q2, q3}
- $\sum$: 字母表,如上面的{0, 1}
$\delta$: 状态转移函数集合,例如
$\delta(q1, 0) = q1 \quad \delta(q1, 1) = q1$
- q0: 初始状态,例如q1
- F: 接收状态集合,{q2}
一些名词:
- 接收字符串: 使状态机最后到接受状态的字符串
- 正则语言: 可以被有限状态机识别的语言
例如:
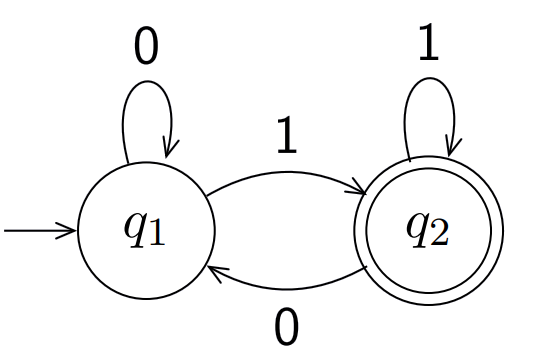
- Q = {q1, q2}
- $\sum$ = {0, 1}
$\delta$:
| Q| 0 | 1|
|-|-|-|
| q1 | q1 | q2 |
| q2 | q1 | q2 |- q0: q1
- F: {q2}
这个状态机的含义是最后的字符时1则接受,如果是0则拒绝。
如果q1是接收状态那么接受集合包括空集和最后字符为0的语言。
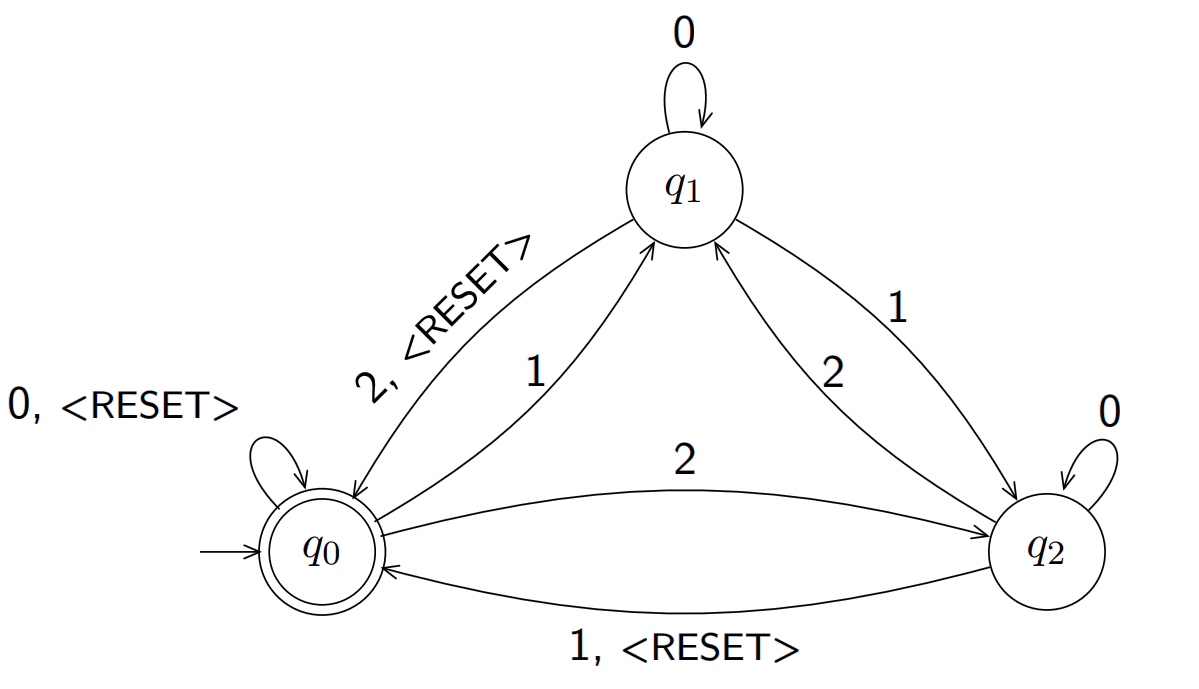
- Q = {q0, q1, q2}
- $\sum$ = {
<RESET>, 0, 1, 2} $delta$:
$\delta(q0, 0) = q0 \, \delta(q0, 1) = q1 \, \delta(q0, 2) = q2 …$
- q0: q0
- F: {q0}
该状态机接受的是累加模三为0的序列,例如123, 121212.并且遇到RESET符号时累加重新计算。
有限状态机计算的标准定义:
- M是一个有限状态机
- w = $a_1 a_2 … a_n 且 a_i \in \sum$
- M接受w当且仅当Q中的状态$r_1 r_2 … r_n$满足下列三个条件
- r0 = q0(从初始状态开始)
- $\delta(ri , a{i+1}) = r_{i+1} i = 0 ,1 … n-1$
- $r_n \in F$
- r0 = q0(从初始状态开始)
正则操作:
假设A和B都是语言,定义正则操作并,拼接, 星:
- 并: $A \cup B = {x | x \in A \quad or \quad x \in B}$
- 拼接: 在上面的基础概念中说明
- 星: 也就是闭包
正则语言在正则操作下是闭包的(操作完后还是正则语言)
非确定性有限状态机
上面讲的是确定性有限状态机。非确定性有限状态意味着一个输入可能会导致多个可能状态。
例如: 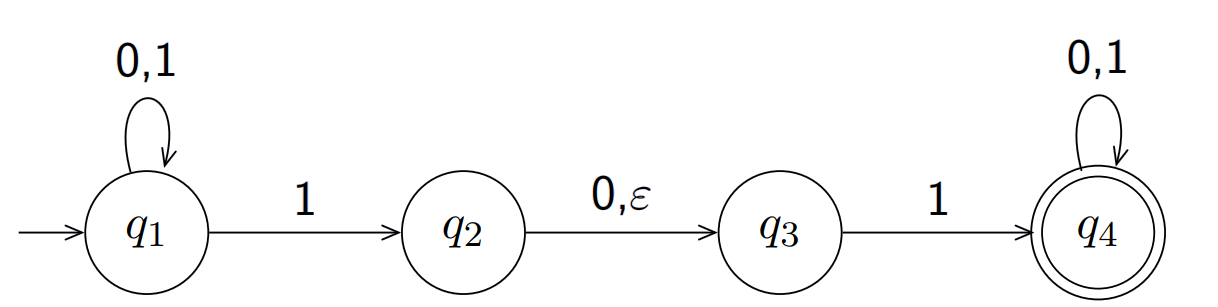
在$q_1$时接受1既可能到1又可能到2。此外$q_2$到$q_3$中的$\varepsilon$表示空串,也就是到了$q_2$可以自动跳转到$q_3$(也可以不跳转)
假设读取一个字符串010110,读取0后状态为$q_1$,读取1后状态为$q_1$或$q_2$或$q_3$(可以认为读取1后继续读取了空串)
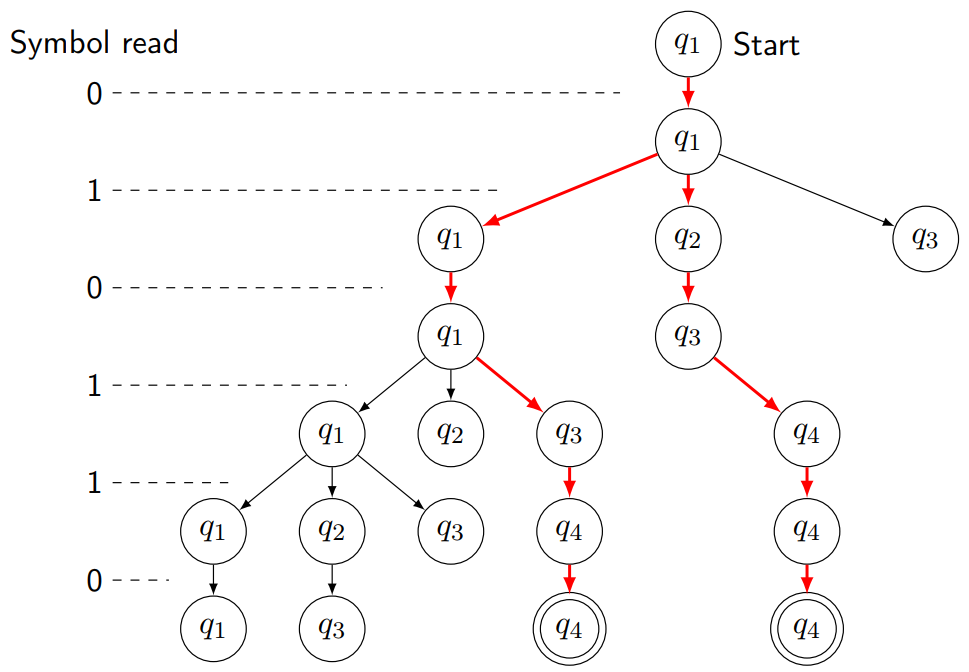
要注意可以有分支死亡,例如第二步读取1后跳转到$q_3$然后继续读取0,q_3不接受0状态因此这个分支死亡。
最后只要有一条分支被接受就可以认为该非确定性有穷状态机被接受。
该状态机的正则语言为$L(N_1 ) = { w | w 包括11或101}$
例2:
使用非确定性有限状态机接受倒数第三个字符为1的字符串。
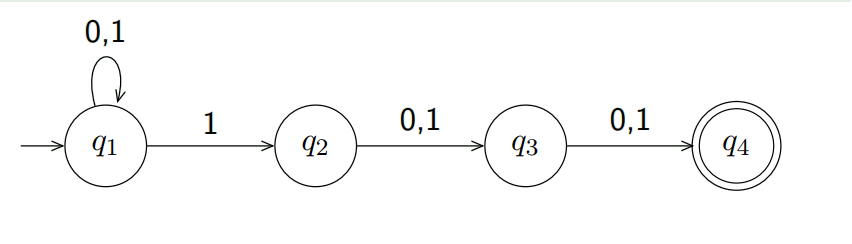
如果中途接受到1,假设为1xxx,那么最后最后一个x时需要从$q_4$转移到另一个状态,因为$q_4$无法转移,因此该分支死亡。之后倒数第三个字符为1最后才能到接收状态。
形式化定义:
一个非确定性有限状态机是一个五元组(Q, $\sum$, $\delta$, $q_0$, F)
- Q: 状态集合
- $\sum$: 输入字母表
- $\delta$: 一个$Q \times \sum -> P(Q)$的状态转移函数。其中P(Q)是Q的幂集。例如第一个例子中的状态转移函数为
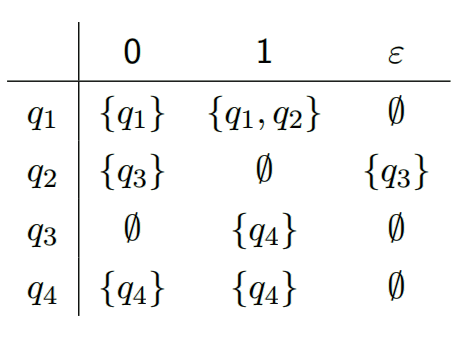
- $q_0$: 初始状态
- F: 接受状态集合
定理: 确定性有限自动机(DFA)和非确定性有限自动机(NFA)等价
等价也就表示他们两个接受相同的语言,虽然看上去NFA更厉害一些,但是他们的能力实际上是相同的。
证明:
- 假设N = {Q, $\sum$, $\delta$, $q_0$, F)是一个接受A语言的NFA
- 我们需要构建一个M = {$Q^{‘}$ , $\sum^{‘}$ , $\delta^{‘}$ , $q_0^{‘}$ , $F^{‘}$)的DFA也识别A。
首先我们不考虑空集的情况。
- $Q^{‘}$ = P(Q) (Q的幂集)
- $\delta^{‘} (R, a) = \bigcup_{r \in R} \delta(r, a)$
- $q_0^{‘} = q_0$
- $F^{‘} = {R \in Q^{‘} | R是Q^{‘} 中包括Q中的任何一项的集合}$
现在我们来考虑包括空集的情况
E( R) = {q | q是当前状态加上沿着空集箭头可以到达的状态集合}
然后$\delta^{‘} (R, a) = \bigcup_{r \in R} E(\delta (r, a))$
例:
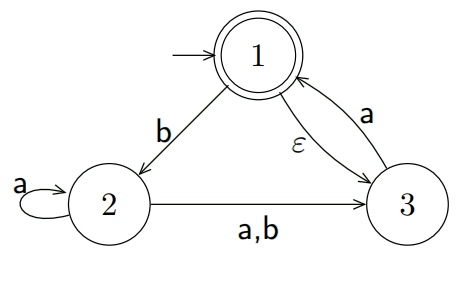
- Q = {$\oslash$ , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
- $\sum$: {a, b}
- $\delta$: $\delta({1}, a)$ = {2}, $\delta$({2}, a) = {2, 3} $\delta$({3}, a) = {1, 3}(因为有空串E(1) = {1, 3}) …
- $q_0$ = 1
- F : { {1} , {1, 2} , {1, 3} , {1, 2, 3}}
生成的图为:
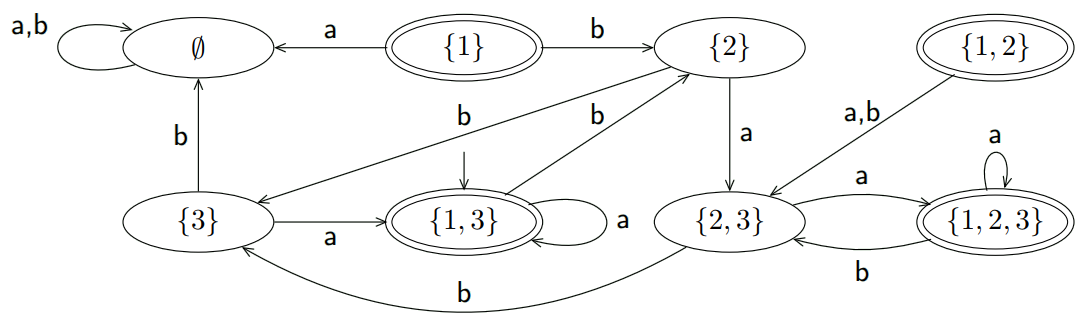
删去只有出没有进的状态得:
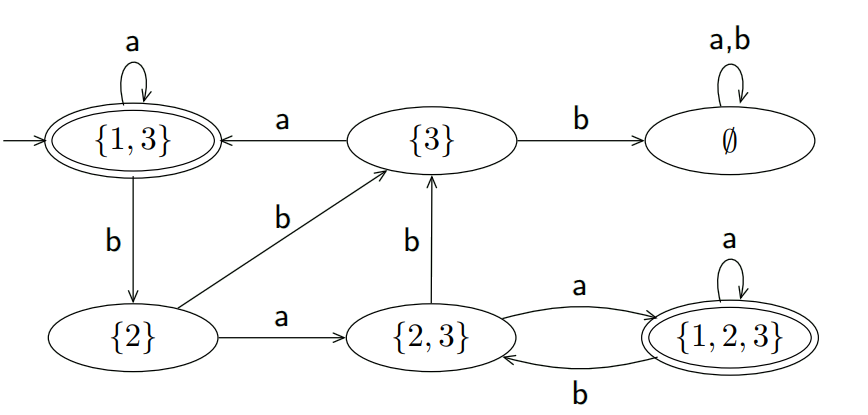
证明正则语言闭包
证明正则语言在$\cup$操作下闭包
假设A1和A2是两个语言,需要构建一个自动机M使得它可以唯一识别$N_1 \cup N_2$的语言。
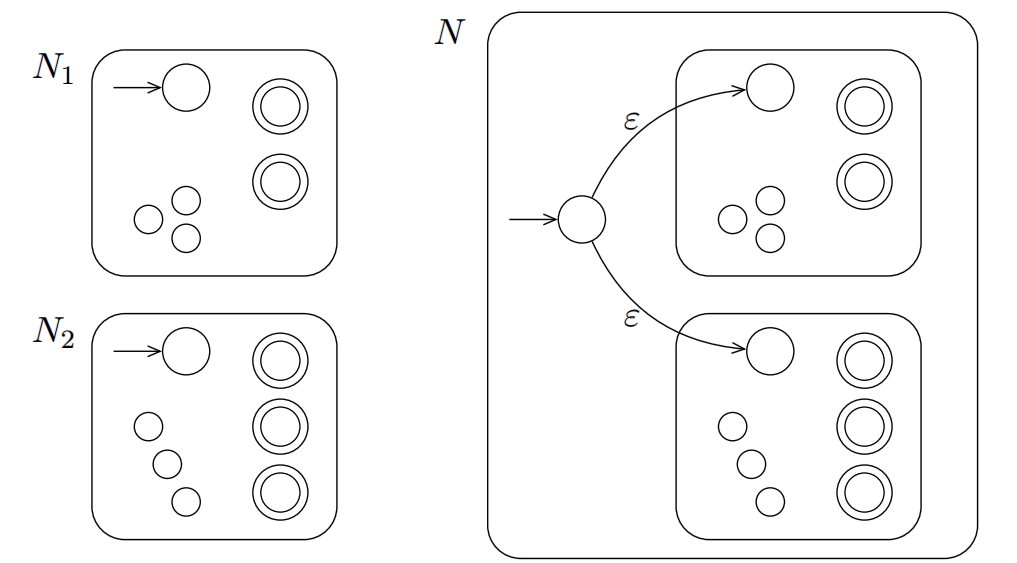
如图所示为NFA的构建方法,因为$N_1 \cup N_2$ 也就是可以接受$N_1$中的语言或$N_2$中的语言,因此只需要同时喂到两台自动机中,只要有一个接受那么最终就接受。
为了达成这个目标,新建了一个起始节点q0,它的作用是同时导入到两台自动机中,方便后面的操作。
形式化定义:
- Q = {q0} $\cup Q_1 \cup Q_2$
- q0是起始状态
- F = $F_1 \cup F_2$
 下面两条其实就是规定起始状态的跳转
下面两条其实就是规定起始状态的跳转
构造完成之后还需要证明它只接受$N_1 \cup N_2$的语言,其他语言都不接受
在拼接操作下闭包
例如 N_1 = {01} N_2 = {00},则二者拼接为{0100}
也就是说到达1之后需要跳转到第二个自动机然后继续执行识别,但是问题是自动机不知道是在哪里拼接,即不知道要在哪个位置跳转,因此使用DFA很难证明。但是在NFA中,只要到达了$N_1$的接受状态就可以跳转,如果不是拼接点到达第二个自动机之后一定不会被接受。
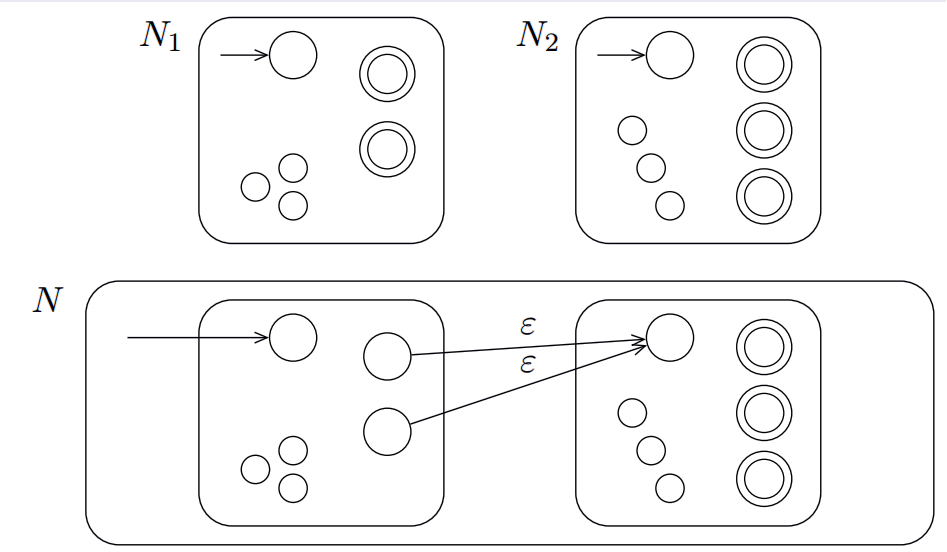
如图所示只需要将$N_1$的接受状态连接到$N_2$的起始状态就可以了。
形式化定义为:
- Q = $Q_1 \cup Q_2$
- 初始状态为$q_1$
- 接受状态和$N_2$相同
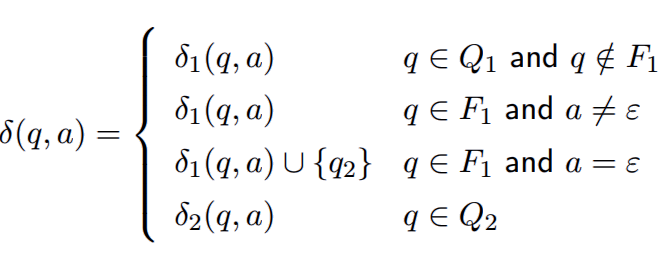 最重要的是第2,3条,如果输入字符为空(任何时刻都可以输入任意多个空字符串)那么额外跳转到$q_2$的起始状态,如果输入不为空则还在$N_1$中
最重要的是第2,3条,如果输入字符为空(任何时刻都可以输入任意多个空字符串)那么额外跳转到$q_2$的起始状态,如果输入不为空则还在$N_1$中
在星操作下闭包
星操作是递归操作,它的递归形式为$L^n = L L^{n-1}$。也就是说每次到接收状态之后会回到初始状态重新接受。例如N = {0, 1}, $N^2$ = {00, 01, 10, 11}。即接收完第一个N后需要回到初始状态接收第二个N。
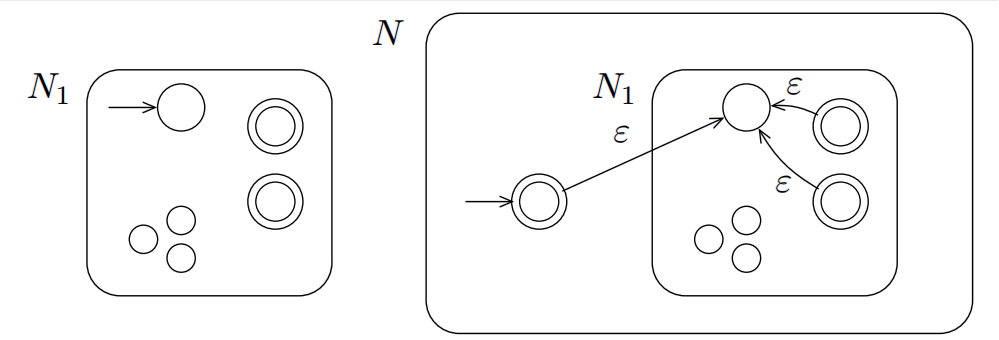
如图所示,每次到接收状态之后都需要到初始状态,因为这有可能是一个分界点。
但是由于闭包中包含$\varepsilon$,也就是说没有输入也会接受。因此初始状态应该称为接受状态。但是在原有初始状态变为接收状态的话可能会出现原来不被接受的字符串现在被接受的情况,因此需要构造一个新的初始状态。
形式化定义为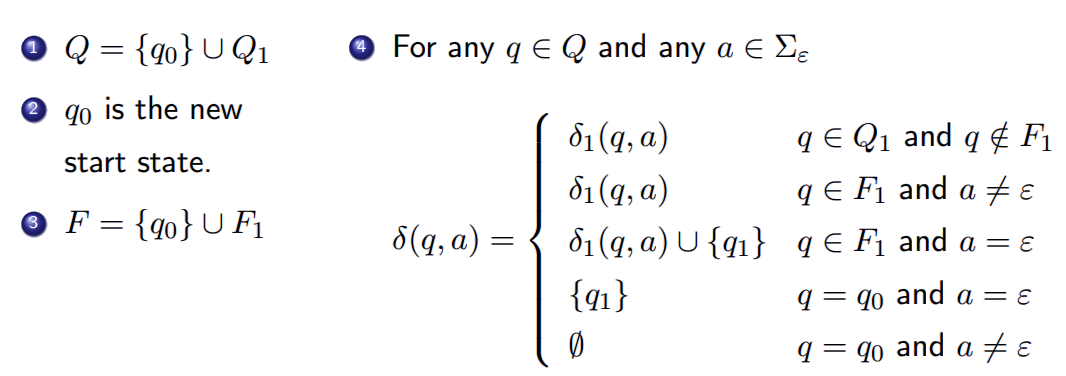
正则表达式
正则表达式的形式化定义为:
- a是正则表达式。a是在$\sum$中的某些字符, $\sum$是所有长度为1的字符
- $\varepsilon$是正则表达式
- $\oslash$是正则表达式
- $(R_1 \cup R_2 )$是正则表示式。其中$R_1 R_2$都是正则表达式
- $(R_1 \circ R_2 )$是正则表达式。
- $R_1^{*}$是正则表达式
需要注意$\varepsilon 和 \oslash$的区别。$\varepsilon$是空串,它在自动机中表示自动跳转。而$\oslash$是空集,表示永远不会跳转。
一些简写:
- $R^+$: 表示$RR^*$
- $R^+ \cup \varepsilon$: 表示$R^*$
- $R^k$: k个R拼接
例如:
假设字母表$\sum = {0, 1}$
- $0^ 1 0^$表示包含一个1的字符串
- $\sum^ 1 \sum^$: 表示至少包含一个1的字符串
- $1^ (01^+)^$: 每个0至少要跟随一个1
- $(\sum \sum )^*$: 偶数长度的字符串
- $(\sum \sum \sum )^*$: 三的倍数长度的字符串
- 01 $\cup$ 10 = {01, 10}
- $(0 \cup \varepsilon ) 1^ = 01^ \cup 1^*$
- $1^* \oslash = \oslash$
- $\oslash^* = {\varepsilon}$
空串和空集涉及的操作:
- $R \cup \oslash = R$
- $R \cup \varepsilon = {R, \varepsilon}$
- $R \circ \oslash = \oslash$
- $R \circ \varepsilon = R$
证明: 正则表达式和确定性有限状态自动机等价
首先证明给出任何一个正则表达式R,我们都可以使用一个有限状态机进行描述
根据正则表达式的定义,我们只需要构造有限状态机识别定义中的每一条即可
- a是正则表达式。a是在$\sum$中的某些字符, $\sum$是所有长度为1的字符.

- $\varepsilon$是正则表达式
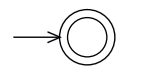
- $\oslash$是正则表达式

至于合并、拼接和星操作在上面已经证明过,这里不再复述
例如一些正则表达式的DFA构建: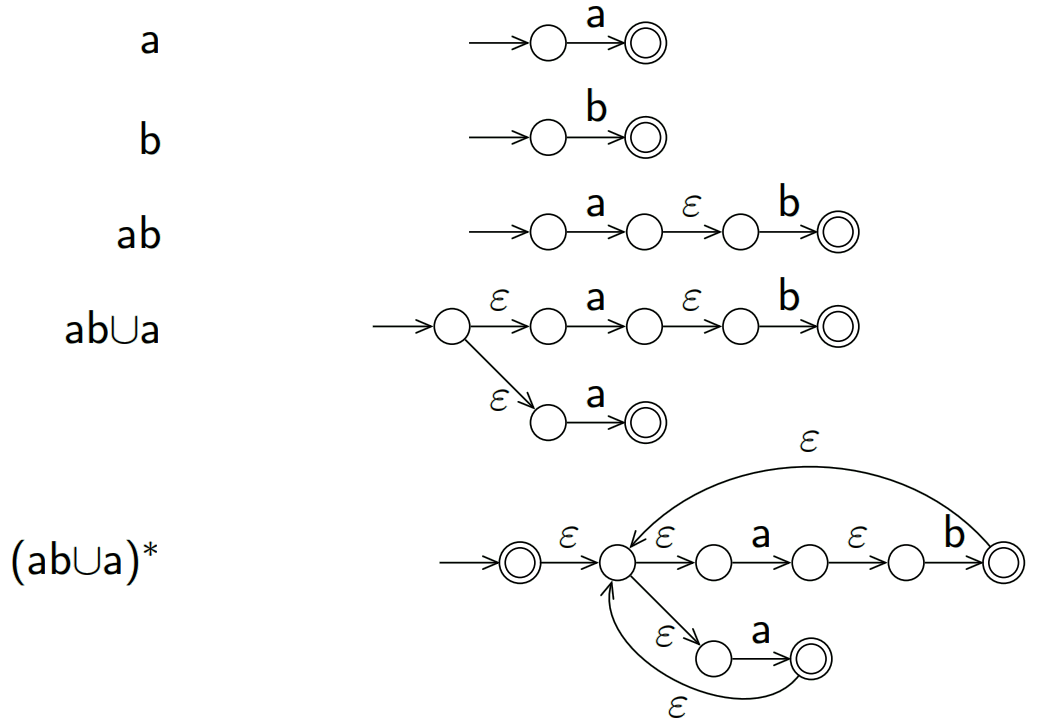
其次证明给出任何一个有限状态机,都可以对应一个正则表达式
为了证明这个,我们首先需要定义广义非确定性有穷自动机(GNFA)。它是一个五元组
- Q: 有限的状态集合
- $\sum$: 字母表集合
- $\delta$: (Q - {$q{accept}$}) $\times$ (Q - {$q{start}$})-> R.也就是除了开始状态只有指向其他箭头,结束状态只有其他状态指向自己的箭头,其他状态必须有指向其他所有状态的箭头。并且R是一个正则表达式,也就是说可以通过正则表达式进行状态转移
- $q_{start}$: 开始状态
- $q_{accept}$: 结束状态,只有一个
例如: 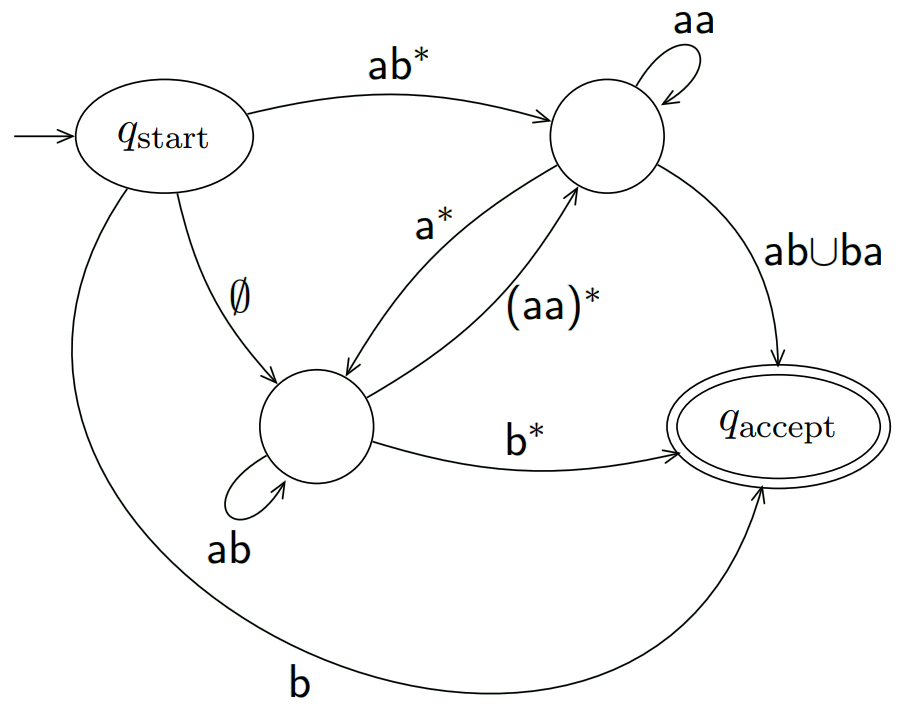
然后我们需要将DFA转换为GNFA再转换为只有开始和接收两个状态的GNFA
- DFA->GNFA:
- 创建一个新的起始状态并且通过空串指向旧的起始状态
- 创建一个新的接收状态让所有老的接收状态通过空串指向这个状态
- 如果某个状态有多个箭头指向另一个状态,那么将这些状态使用$\cup$进行合并并使用一个箭头指向
- 所有没有没有箭头连接的状态之间使用$oslash$进行连接
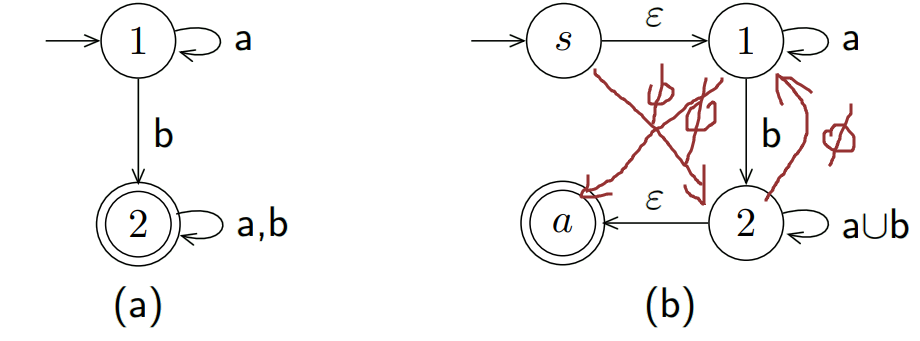
- 创建一个新的起始状态并且通过空串指向旧的起始状态
- GNFA->2状态GNFA:
- 假设GNFA中状态数为k
- 如果k>2则删除一个除起始和结束状态之外的状态,记为$q_{rip}$
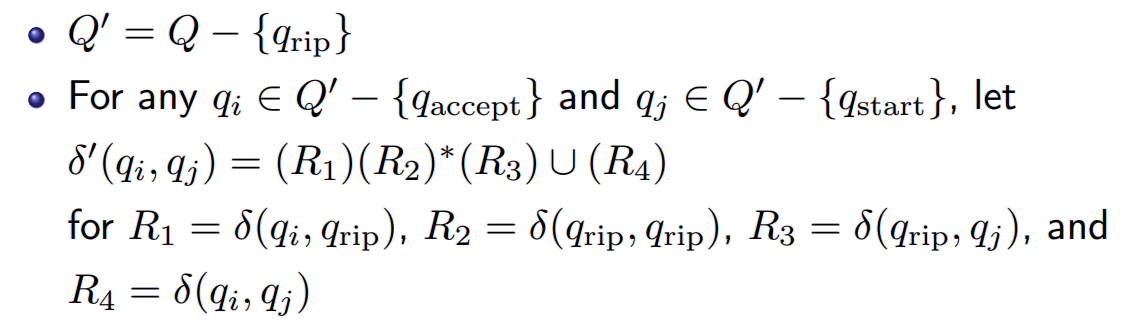
- 如果k=2则停止,它接受的语言就是从起始状态到接收状态之间的正则表达式
- 如果k>2则删除一个除起始和结束状态之外的状态,记为$q_{rip}$
- 假设GNFA中状态数为k
例如: 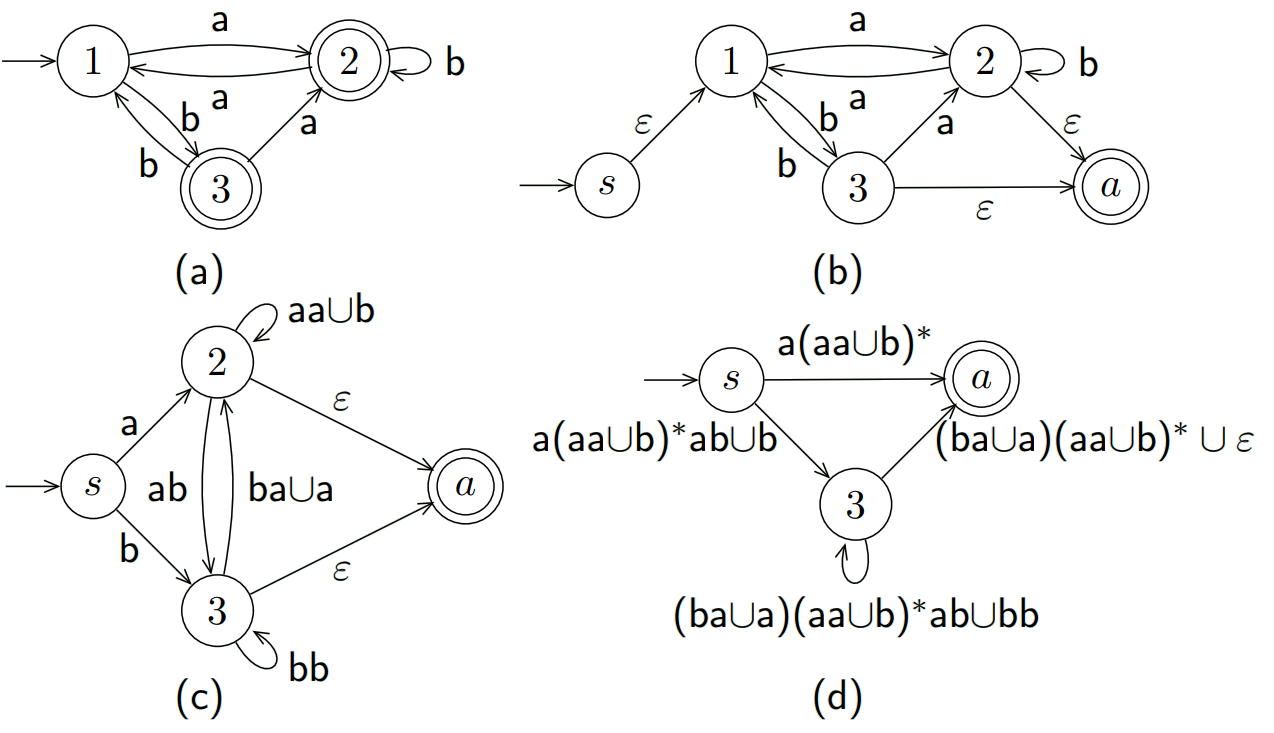
首先从b状态转换到c状态,删去1。重新构建所有关系。
考虑s, s到2为$\oslash$,s经过1到2为 $\varepsilon \cup \varepsilon \cup a = a$最后取并集$\oslash \cup a = a$。其他状态同理
删去2:
- 考虑s,s到3为b,s经过2到3为$a (aa \cup b)^ ba \cup a$,综合起来为$b \cup (a(aa \cup b)^ ba \cup a)$
- 考虑3, 3需要额外注意的是自己到自己。3到3为bb,3经过2到3为$ab(aa \cup b)^ ba \cup a$合并起来为$bb \cup (ab(aa \cup b)^ ba \cup a)$
泵引理
是否所有语言都可以用有限自动机进行描述呢?
例如语言B = {$0^n 1^n | n > 0$}就无法使用优先自动机进行描述,因为有限自动机的状态是有限的,而B语言可能的状态是无限的
但是不是所有看起来是无限状态的自动机都不可以用有限自动机进行描述。例如:D = {w有相同的1和0的数量}。这个便可以使用有限自动机进行描述
泵引理就是所有有限自动机都有的一个性质,可以通过他来判断一个自动机是否是有限自动机。
定理
假设A是一个正则语言,于是有这样一个数字p(泵长度)使得存在A中长度超过p的字符串s,它可以被分成三个部分s = xyz,并且满足下列性质:
- 对每个i>=0, $xy^i z \in A$,且xz也是可以被接受的
- |y| > 0 (y不能是空串)
- |xy| $\le$ p (xy的长度小于等于p)
p为状态机中的状态数,如果A中所有字符串长度都小于p,那么它一定可以被有限状态机描述。
证明
- 首先让p是状态机M中的状态数
- 哦们假设s是A中长度大于等于p的一个字符串,并且他可以被分为三个部分xyz,满足上面三条性质
- 首先$s \ge p$,因此经历的状态数一定大于等于p+1(因为起始状态没有接收任何字符串).
- 因此一定会重复进行某个状态,我们假设第一次重复状态之间的的字符串为y,前面的字符串为x,后面的字符串为z。
- 因为输入p个字符串一定会有重复,因此可以断定|xy| $\le$ p
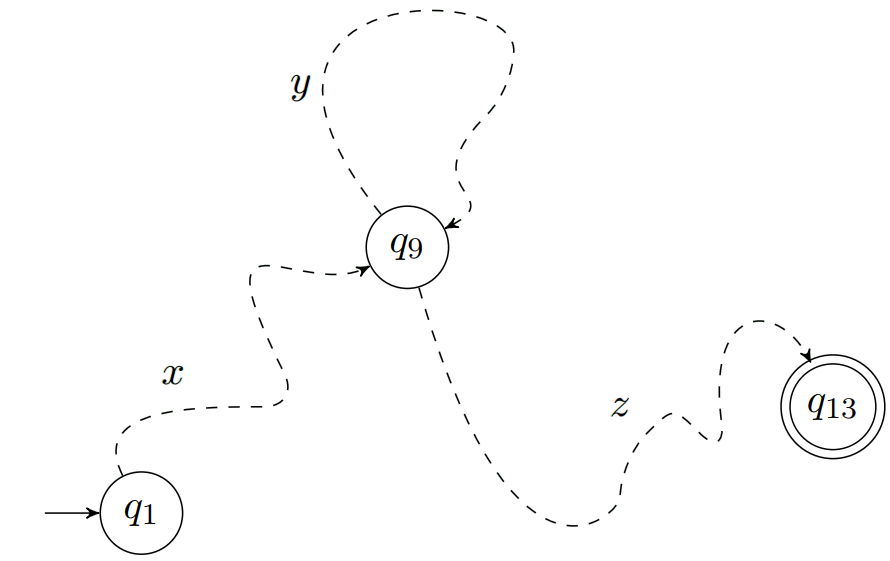
利用泵引理证明一个状态机不是有穷状态机:
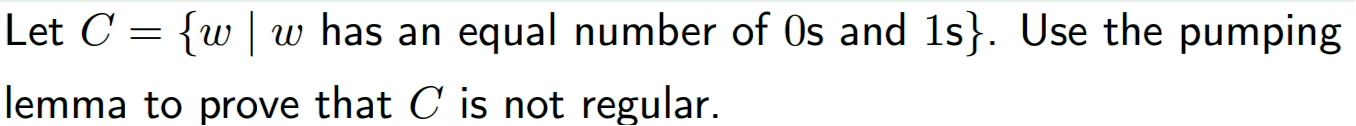
解: 假设有p个状态,令s = $0^p 1^p$
y总共有三种状态,全是0,一半是0一半是1,全是1.首先由于$xy^i z \in A$因此排除全是0和全是1的可能,一半是0一半是1的可能由于xy长度超过p因此也不可能。s违背了泵引理,因此该状态机不是有穷状态机

构造s = $0^p 1 0^p 1$.因为长度要小于p,所以抽取字符串只可能是若干个0。被抽取字符串后xz无法被有穷自动机识别,因此不满足泵引理。
正则语言的性质
我们之前已经考虑过在并,连接,星操作下的封闭性,现在我们还要考虑交、补、差、逆转、同态、逆同态下的封闭性。
补
正则运算在补运算下封闭,即若L是字母表$\sum^$上的正则语言,则$\sum^ - L$也是正则语言。
证明:
如果L可以被某个DFA(Q, $\sum$, $\delta$, $q_0$, F)识别,那么L中的字符串会到接收状态,也就是说不在L中的字符串不会到接收状态。因此只需要构造$Q^{‘} = Q, \sum^{‘} = \sum , \delta^{‘} = \delta , q_0^{‘} = q_0 , F^{‘} = Q - F$
交
$L_1 L_2$是两个正则语言,证明$L_1 \cap L_2$也是正则语言
证明:
$L_1 \cap L_2$是正则语言表明这个字符串沿着两个语言的自动机走都可以到达接受状态,因此我们可以构造一个新的自动机M同时考虑两个状态。
- Q = $Q_1 \times Q_2$
- $\sum$ = $\sum$
- $\delta$ = $\delta((q_i , q_j ), a) = (\delta (q_i , a) + \delta (q_j , a))$
- $q_0 = (q_1, q_2 )$
- F = $F_1 \times F_2$
也可以通过集合的方式证明,$L_1 \cap L_2$ = $\bar{L_1} \cup \bar{L_2}$,而$\bar{L_1} 和 \bar{L_2}$封闭,$\cup$封闭,因此原式也封闭
差
证明$L_1 - L_2$也是正则语言
$L_1 - L_2 = L_1 \cap \bar{L_2}$,而$\bar{L_2}$封闭,$\cap$运算封闭,因此原式封闭
逆转
若L是正则语言,则$L^R = {x | x^R \in L}$也是正则语言。其中$L^R$是将L中的每个字符都逆转过来形成。
证明:
基于有穷自动机的证明
存在一台有穷自动机(Q, $\sum$, $\delta$, $q_0$, F)识别L,现在要构造一台有穷自动机$Q^{‘} , \sum^{‘} , \delta^{‘} , q_0^{‘} , F^{‘} $识别$L^R$由于是逆转,因此可以看成从终点状态到起点状态,由于终点状态不唯一,因此可以新构造一个状态,然后通过$\varepsilon$指向原来的终点状态并将所有连线的指向逆转。
基于正则表达式
基于正则表达式可以使用归纳假设的方法.L可以通过一个正则表达式E表示,根据E我们可以构造$E^R$来表示$L^R$- 当构造次数为0,则E = $\varepsilon$, $oslash$或者$\sum$中的某个符号a。而这三个数的逆转还是他们自身,因此$E^R = E$
- 假设当构造次数小于k时,可以通过E构造$E^R$表示$L^R$,现在考虑构造次数为k时,仍然可以得出下面结论。需要考虑三种情况(1) E = $E_1 \cup E_2$ (2) $E_1 \circ E_2$ (3) $E_1^*$
因此$E^R = E_1^R \cup E_2^R$是$L(E)^R$的正则表达式1. $L(E_1 )^R = L(E_1^R )$,$L(E_2 )^R = L(E_2^R )$(因为$E_1^R$生成的语言正好是$L_1^R$.又因为$L(E) = L(E_1 ) \cup L(E_2 )$,所以$L(E)^R = L(E_1 )^R \cup L(E_2 )^R = L(E)^R = L(E_1^R ) \cup L(E_2^R )$.
$\circ$的证明同理- 的归纳。我们最终需要证明$(E_1^R )^$ 是$L(E1 )^R$的正则表达式,证明过程为
$E = E_1^ , L(E_1^R ) = L(E_1 )^R$, L(E) = $L(E_1^ )$,假设L(E)中的字符串w为$w_1 w_2 … w_n$,则$w^R = w_n^R w{n-1}^R … w_1^R$,$w_i^R \in L(E_1 )^R = L(E_1^R )$,所以 $w^R \in L((E_1^R )^* )$
- 的归纳。我们最终需要证明$(E_1^R )^$ 是$L(E1 )^R$的正则表达式,证明过程为
同态
设$\sum \bigtriangleup$是两个字母表,h是$\sum -> \bigtriangleup^$的全映射,对于任何x,y $\in \sum^$都有 h(xy) = h(x)h(y),则称h为$\sum 到 \bigtriangleup^*$的全映射。
- 同态像: 对于所有L $\in \sum^$, L的同态像是$\bigtriangleup^$的一个子集,定义为h(L) = $\bigcup_{x \in L} {h(x)}$
- 同态原像: 对于所有w $\in \bigtriangleup^$, w的同态原像是$\sum^$的一个子集,定义 $h^{-1}(w) = {x | h(x) = L}$
- 逆同态: 对于$L \in \bigtriangleup^*$, L的同态原像是 $h^{-1}(L) = {x | h(x) \in L}$
例如:
我们需要证明如果L是字母表$\sum$上的正则语言,h是$\sum$到$\bigtriangleup$上的一个同态映射,证明h(L)是$\bigtriangleup$上的正则语言
证明:
同样使用归纳证明。L = L(R),R是$\sum$上的正则表达式,h(R)是将R中的每个符号使用h(a)代替形成的正则表达式,我们需要证明L(h(R)) = h(L(R))
- 构造次数为0时,R仅可能是$\varepsilon , \oslash$和字母表中的任意一个字符。对于前两种情况,显然相同。
对于最后一种情况。L(R) = {a}, h(L(R)) = {h(a)}.而h(R) = h(a), L(h(R)) = {h(a)},因此L(h(R)) = h(L(R)) - 对于构造次数为k,根据外层构造,可能有三种情况
- R = F $\cup$ G.
L(h( R)) = L(h(F $\cup$ G)) = L(h(F) $\cup$ h(G)) = L(h(F)) $\cup$ L(h(G))
h(L( R)) = h(L(F) $\cup$ L(G)) = h(L(F)) $\cup$ h(L(G)).而L(h(F)) = h(L(F)),L(h(G)) = h(L(G)).所以L(h( R)) = h(L( R))
其他情况类似证明方式
- R = F $\cup$ G.
逆同态
如果L是字母表$\bigtriangleup$上的正则语言,证明$h^{-1}(L)$是$\sum$上的正则语言
正则语言的判定
具有n个状态的有穷自动机具有下列性质:
- 接受语言非空,当且仅当它接受一个小于n的字符串
- 接受语言是无穷集合,当且仅当它接受一个长度在[n, 2n]的字符串
证明可以根据泵引理
根据上面的两个性质我们可以做出如下判定:
- 给定一个有穷自动机,L(M)是否为空是可以判定的:
因为长度小于n的字符串个数是有穷的,因此逐个检验字符串是否被有穷自动机接受即可判定接受语言是否非空 - 给定一个有穷自动机,L(M)是否是有穷集合是可以判定的。
利用性质2即可。 - 两个自动机等价是可以判定的:
假设L($M_1$) = $L_1$, L($M_2$) = $L_2$。设计一个接受L = $(L_1 \cap \bar{L_2}) \cup (\bar{L_1} \cap L_2 )$的有穷自动机M。因为L = $\aslash$ => $L_1 = L_2$,因此只需要判定L接受语言是否为空就可以判定两个自动机是否相同。
有穷自动机的最小化
对于给定的DFA M = (Q, $\sum$, $\delta$, $q_0$, F),定义等价关系如下:
对于p,q $\in$ Q.若对于任意w $\in \sum^*$, $\bar{\delta}(p, w) \in F 当且仅当 \bar{\delta}(q, w) \in F$,则称p和q等价,或者p和q不可区分。
不要求$\bar{\delta}(p, w) 和 \bar{\delta}(q, w)$是相同状态,只要是接受状态都可以。
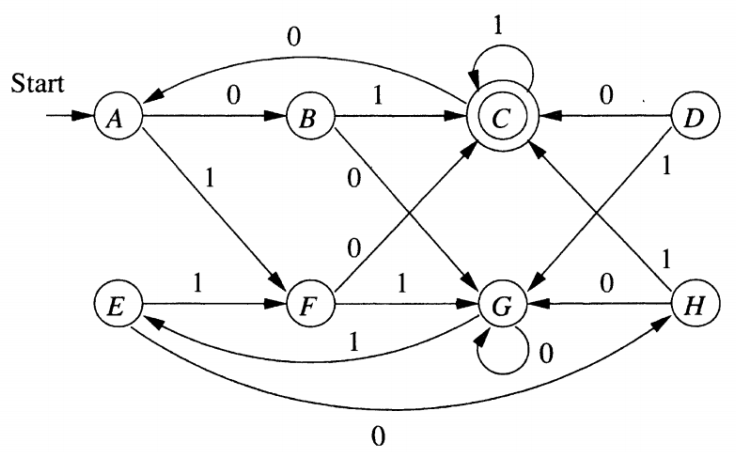
例如A和G, A接受两个0后会到G状态,此时G还在G状态,因此最后会同时到接受状态,因此二者不可区分。但是C和G找不到一个字符串使他们分开,因此二者可区分。
我们需要找到所有不可区分的状态对,将他们合并就可以得到最小自动机。
填表算法
- 基础: 如果$p \in F$并且$q \notin F$,则二者可区分。然后将(p, q)进行标记
- 递归: 重复下列过程知道不再改变。如果若存在未标记状态(p, q),且存在一个$a \in \sum$,且{$\delta (p, a), \delta (q, a)$}被标记,则将(p, q)标记
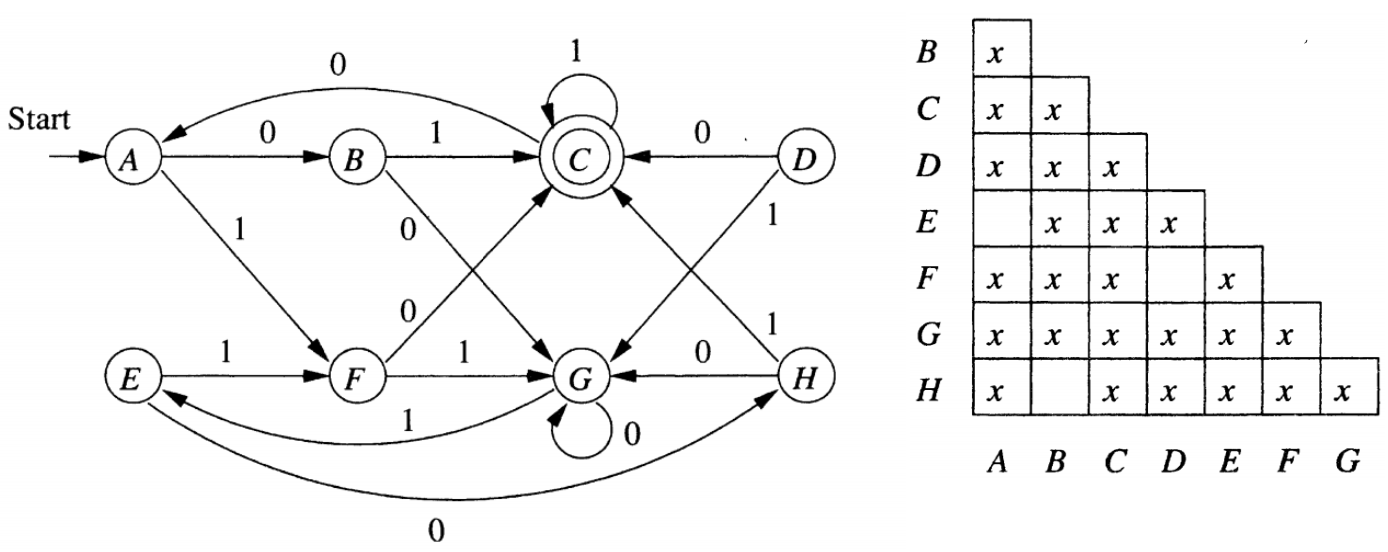
获得了不可区分状态对后,根据等价状态对,将他们划分成状态块,也就是构成一个新的有限自动机,其中:
- $Q^{‘}$ = { p | p $\in$ Q}
- $\delta^{‘}(p, a) = \delta(p, a)$
- $q_0^{‘}$ = $q_0$
- $F^{‘}$ = {p | p $\in$ F}
也就是将合并后状态中的任意一个状态转移作为这个新状态转移,因为他们是等价的。
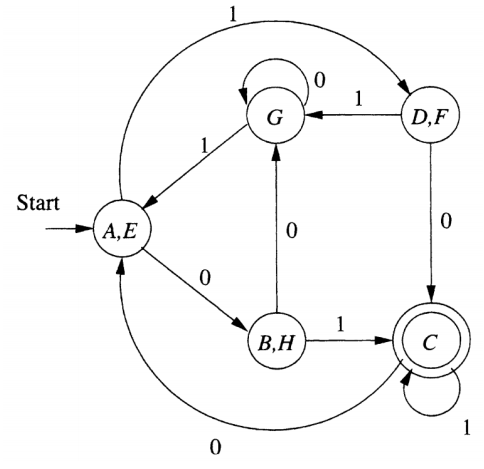
正则文法
形式化定义:
一个文法就是一个四元组G = (V, T, P, S)
- V是变元的有限集
- T是终结符的有限集
- P是产生式的有限集。每个产生式是 a -> b的形式,其中a $\in (V \cup T)^+$,且至少有一个V中的符号。b $\in (V \cup T)^*$
- S是开始符号
例如 
其中<Sentence>, Article>等是变元,而the, a等是终结符.
要写一个文法,只需要给出产生式即可,文法的四个条件都在产生式中体现。
- 直接推导: 例如 a = $a_1 a_2 a_3$, b = $b_1 \beta b_3$并且由$a_2 -> \beta$是一条产生式,由a => b就可以称为直接推导
- 推导:运用了多次直接推导推出最后结果。记作$\alpha \overset{*}{\Rightarrow} \beta$
乔姆斯基范式
三型文法(正则文法)所有产生式都有如下形式:
- A -> a
- A -> aB
其中 a $\in T \cup {\varepsilon}$, A, B $\in$ V。
定理: 有穷自动机和正则文法等价
如果L可以被某个正则文法产生,那么他可以被某个有穷自动机接受
构造一个NFA {$v \cup {f}, T, \delta , S , {f}$}
$\delta(B, a)$ = {C | 对于所有产生式B->aC} $\cup$ {f | 对于所有B->a $\in$ P}
$\delta$(f, a) = $\oslash$
自动机中的状态是文法中的变元。每次接收到A->aB类型的文法时都会进行跳转,而如果是A->a说明可能到了最后的状态,因此跳转到接受状态。
例如一个正则文法为:
S->0B
B->0B | 1S | 0
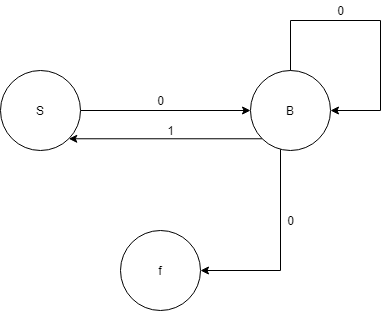
如果L可以被DFA接受,那么他可以被某个正则文法产生
已知DFA M={Q, $\sum , \delta , q_0$, F},构造正则文法G(V, T, P, S)
- S = q_0
- T = $\sum$
- V = Q
- P = $\delta(B, a) = Q$,则将B->aQ加入P.如果$\delta(B, a) \in F$,则将B->a加入P