马尔可夫模型
本文最后更新于 2024年10月1日 上午
定义
系统中有若干个状态S1, S2, …, Sn. 随着时间推移,系统会从一个状态转移到另一个状态,马尔可夫模型认为后一个状态和前面若干个状态有关系。

例如天气和前面若干天的天气之间有关系,假如近两天天晴明天天晴的可能性就比较大。
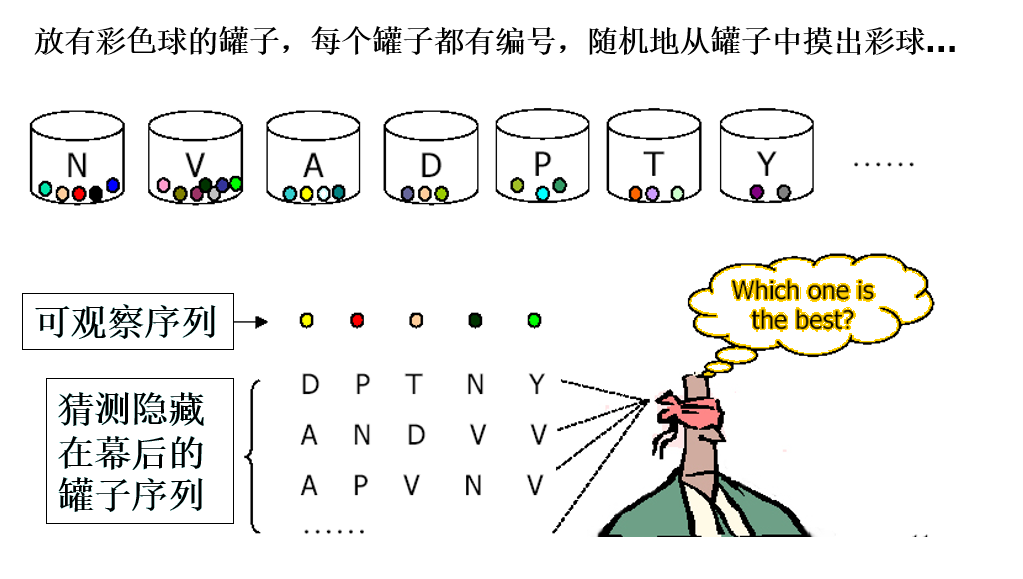
形式化描述:
马尔可夫模型可以表示为一个五元组$\lambda = (S, O, A, B, \pi)$
- 状态集合S: S = {S1, S2, S3} 描述了模型所有可能的状态,例如上例中{下雨,天晴,刮风…}或{N, V, A, D, P, T, Y}
- 输出符号集合O: 所有状态输出的集合。例如上面不同颜色的小球
- 状态转移矩阵A = $a_{ij}$
 。它决定下一个状态。
。它决定下一个状态。 - 可观察符号的概率分布矩阵B = $b_j (k)$: 表示在状态j输出符号为k的概率。它决定在当前状态输出什么符号
- 初始状态概率分布$\pi$: 最开始可能位于什么状态.

两个假设
齐次马尔可夫假设
也就是说当前状态只和前一个状态有关,和其他状态和观测无关,形式化描述为:
观测独立假设
当前观测只依赖于当前状态,和其他观测及状态无关:
评估问题
评估问题是给出一个序列$O = O_1 O_2 … O_n$ 和模型$\lambda$,计算在该模型下观察到O的概率P(O | $\lambda$)
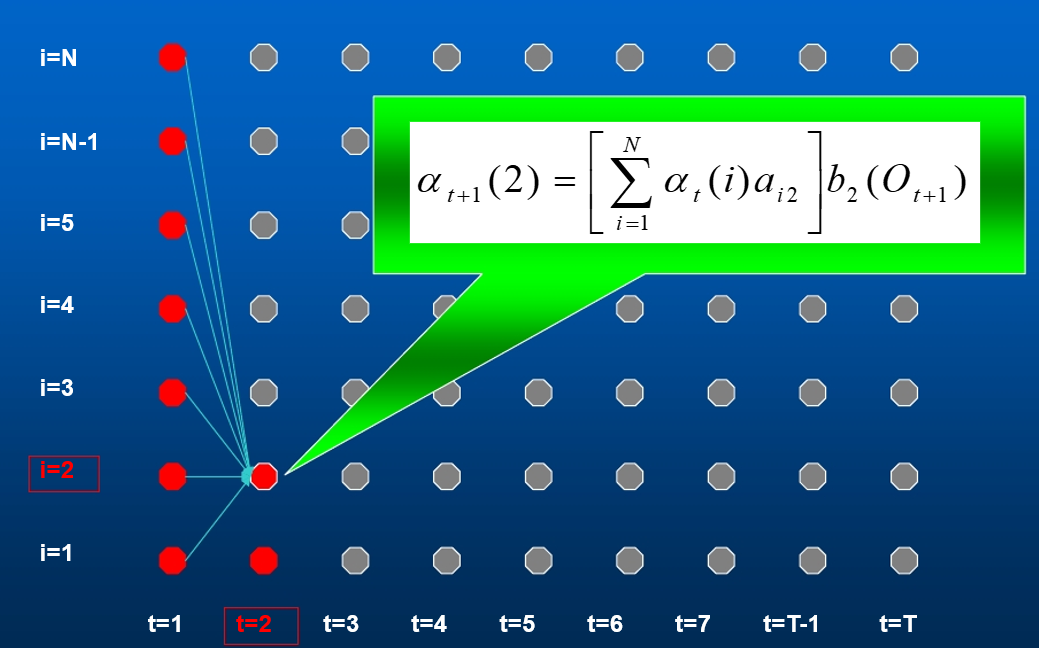
假设模型在时间t的输出序列为$O_1 O_2 … O_t$, 并且位于状态i的概率为
则
由上面的公式可以推得一个递推过程,从$a_1 a_2$到$a_T$,然后得出最终结果
算法过程为:
- 初始化: $\alpha_1 (i) = \pi_I b_i (O_1 ) , 1 \le i \le N$
- 递归:
从结果上看$a{t+1}(j)$就是从上一个状态跳转到j状态的可能性乘上j状态得到O{t+1}的可能性
- 终止: $P(O | \lambda) = \sum_{i=1}^{N} \alpha_T (t)$
例如:
解码问题
给定一个观察序列$O = o_1 o_2 … o_n$和模型λ,如何计算状态序列$Q = q_1 q_2 … q_r$,使得该状态序列能“最好地解释”观察序列。
它的一个典型应用是词性标注问题,在这里面词性就是状态,而观察序列O是输入句子,在这里问题变成了如何确定句子中每一个词的词性(确定最优的Q)。
Viterbi变量
Viterbi变量表示的是在t时间沿状态序列$q_1 q_2 … q_t$产生出$O_1 O_2 … O_n$的最大概率
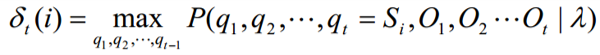
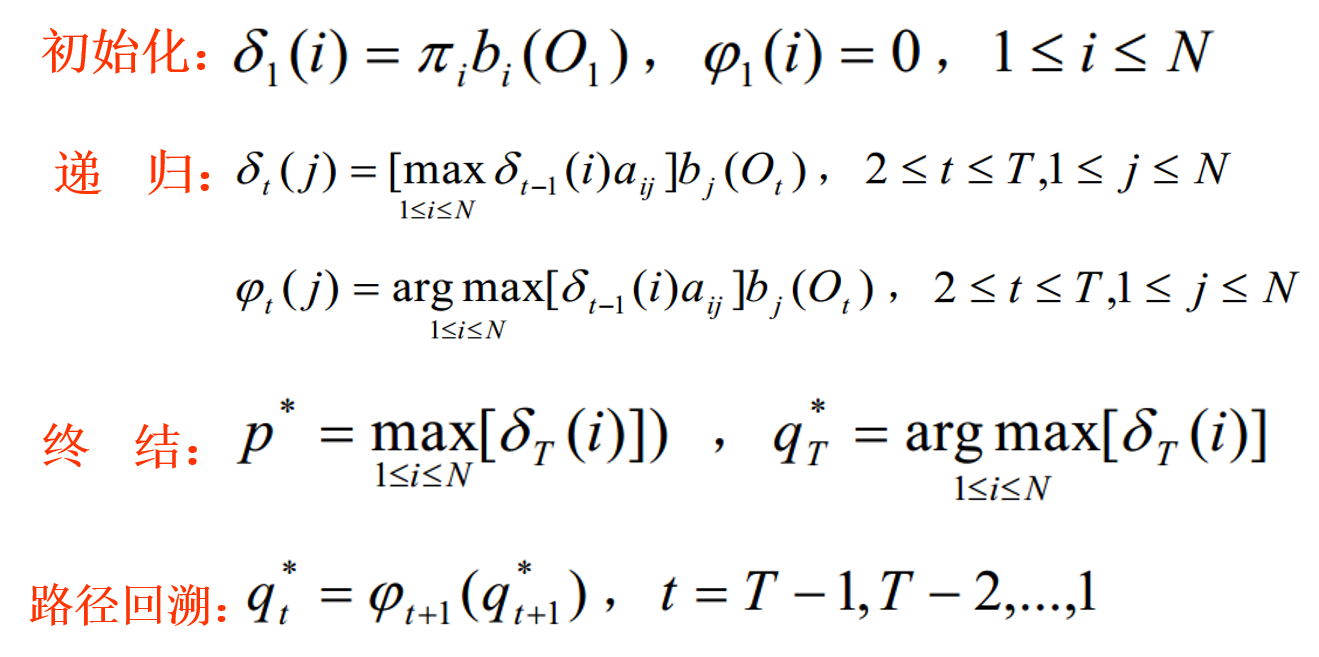
其中argmax表示的是使$\delta_t (j)$值最大的i。
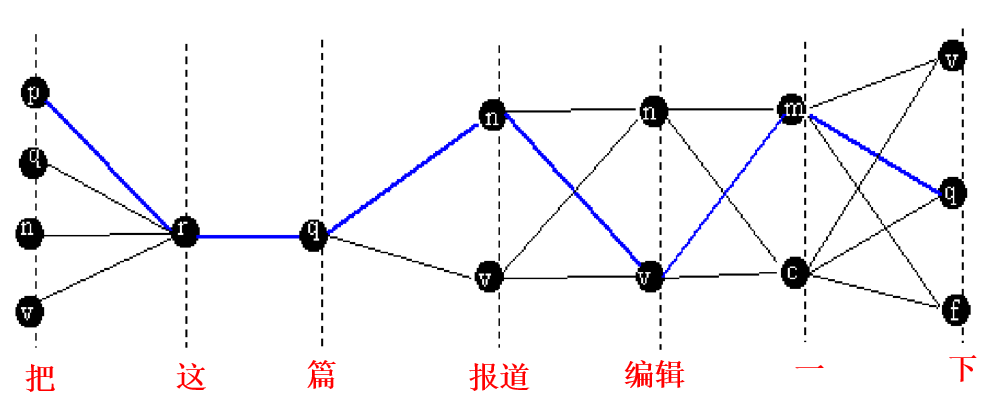
例如从把到这有四条路径,其中第一条路径的点值是最大的,因此$\phi2 (1)$的值是$a{00}$
词性标注问题中A矩阵和B矩阵获得
A矩阵也就是词性转移矩阵,词性转移矩阵的计算公式为:
B矩阵表示的是某个词为某种词性的概率:
EM算法


获得了$\alpha$和b后我们就可以进行估计了
$\xi_t (i, j)$表示当前时刻在i状态,下一时刻在j状态的概率
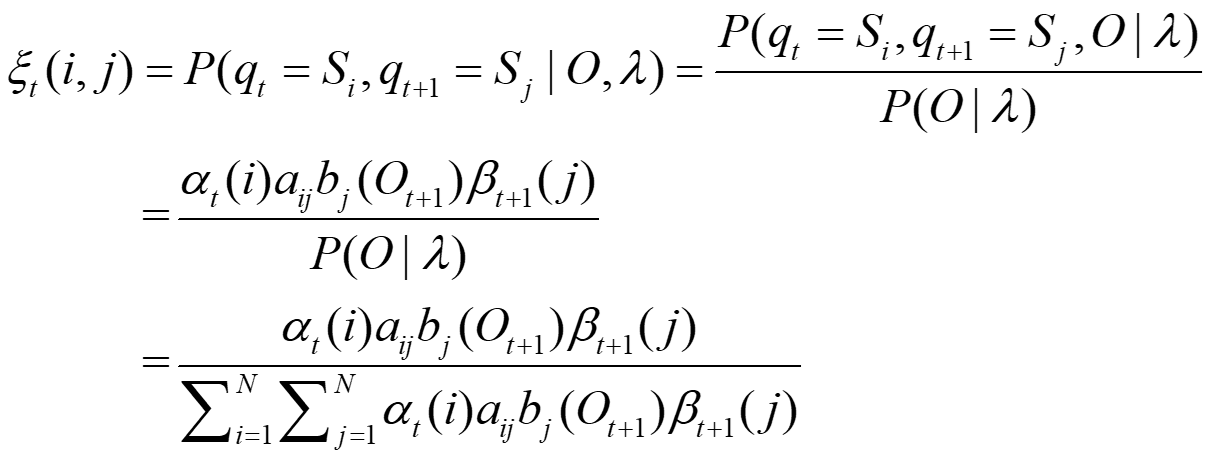
$\gamma_t (i)$表示t时刻咋t状态的概率
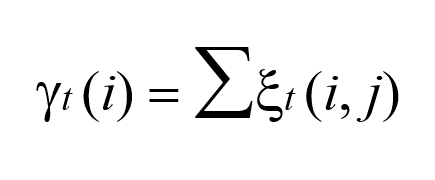
通过前面的式子我们计算出了$\xi 和 \gamma$,通过这两个变量我们可以估计$\alpha$和b


然后再用计算出来的$\alpha$和b计算$\xi 和 \gamma$。不断来回计算