线和面的表示
本文最后更新于 2024年10月1日 上午
线的表示
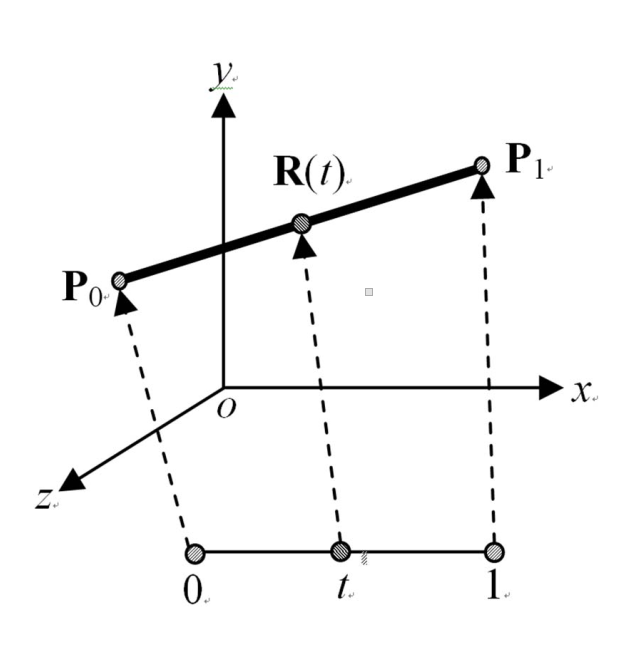
定义: P1(x1, y1, z1) P2(x2, y2, z2)是空间中的两点,两点之间线段的表示为;
这种表示方法的优点在于他只有一个变量,并且范围始终在[0, 1]。这也使得我们可以通过改变线的大小方便的得到不同的点从而在计算机中绘制出这条线。
一般式:
二维线画图元生成
直线段生成
DDA算法
依据:y = m * x + b
其中 $m = \frac{y_2 - y_1 }{x_2 - x_1 }, b = y_1 - m * x_1$
现在需要从(x1, y1)到(x2, y2)间画线
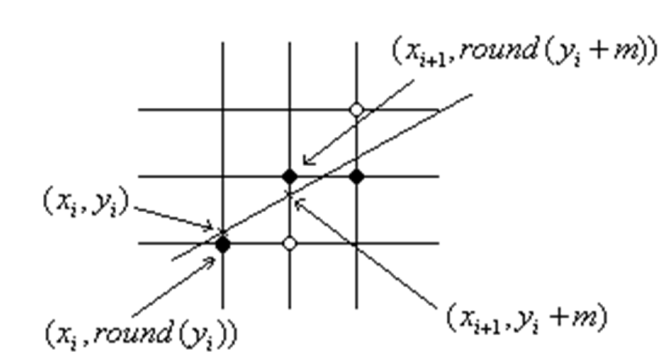
算法步骤:
- 划分区间[x1, x2] x1, x2, …, xi, …, xn 其中$x_{i+1} = x_i + 1$
- 计算每个点的纵坐标,通过下面的方法可以让原来的乘法计算变为加法,增快速度。其中$m \in [0, 1]$
- 取整: $y{i+1} = round(y{i+1}) = (int)(y_i + m + 0.5)$。并且这是向下取整.
当m > 1时, 需要将x轴和y轴调换位置,也就是区间是[y1, y2],而计算的是x。因为斜率大于1可能出现x增加一格而y增加2格以上的情况,这样就会使线有空隙。
当m < 1时, dx或dy 为 -1,也就是区间为[y2, y1]
实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46void MainWindow::line_DDA(QPoint point1, QPoint point2, QColor color)
{
if(point1.x() > point2.x())
{
swap(point1, point2);
}
int dx = point2.x() - point1.x();
int dy = point2.y() - point1.y();
int steps = 0;
if(abs(dx) > abs(dy))
{
steps = abs(dx);
}
else
{
steps = abs(dy);
}
float inc_x = (float)dx / (float)steps;
float inc_y = (float)dy / (float)steps;
QList<QPoint> list;
list.append(point1);
float x = point1.x();
float y = point1.y();
for(int i=0; i<steps; i++)
{
x += inc_x;
y += inc_y;
list.append(QPoint((int)(x+0.5), (int)(y+0.5)));
}
line l;
l.begin_point = point1;
l.end_point = point2;
l.points = list;
int r, g, b;
color.getRgb(&r, &g, &b);
if(r == 255 && g == 255 && b == 255)
{
l.color = now_color;
}
else
{
l.color = color;
}
line_points.append(l);
update();
}
Bresenham算法
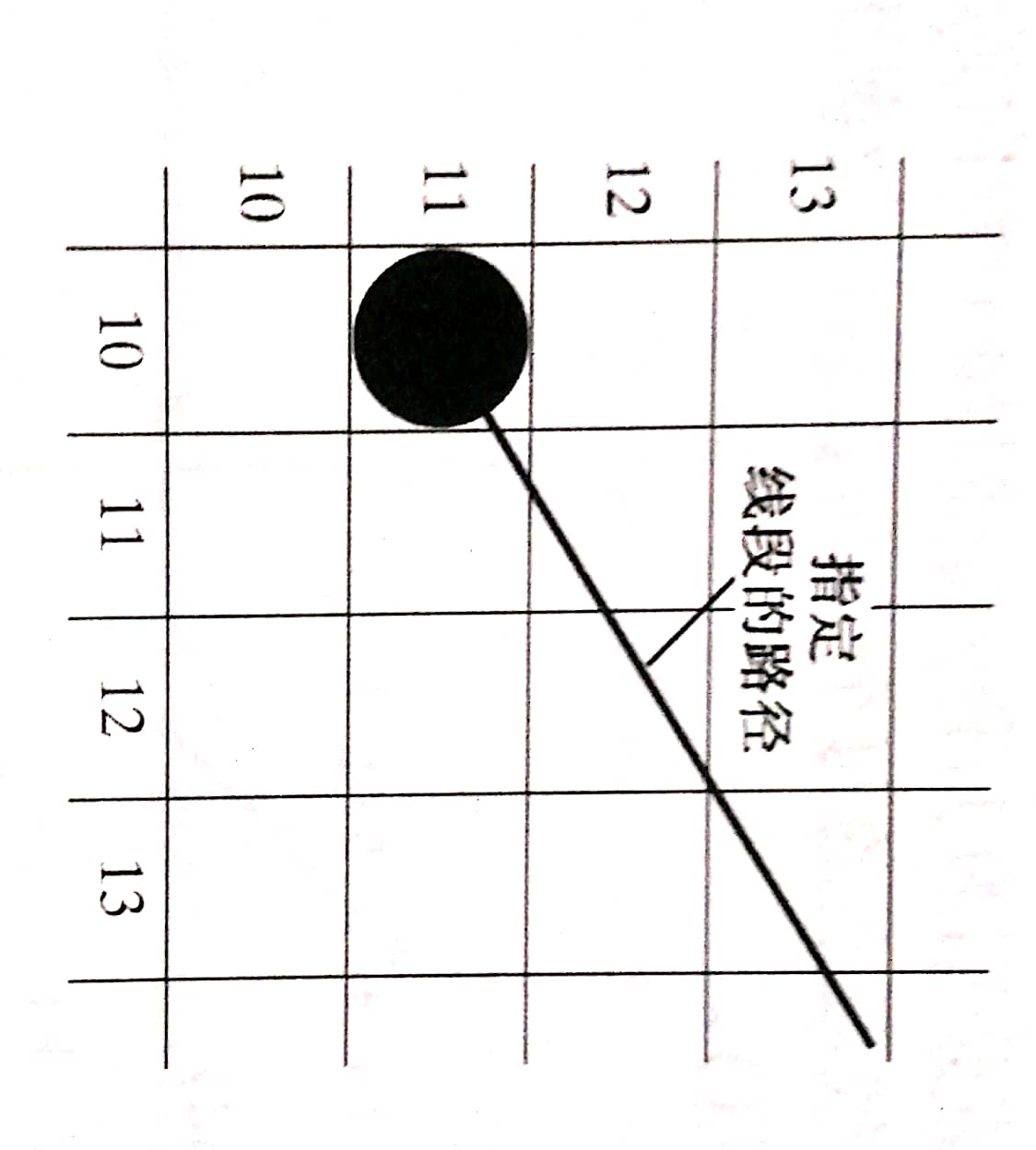
它的基本思想是根据当前节点估计后继节点,图中后继节点只有两个(11, 11)和(11, 12)。它只有加法运算,实现在运用最广泛的直线扫描算法。
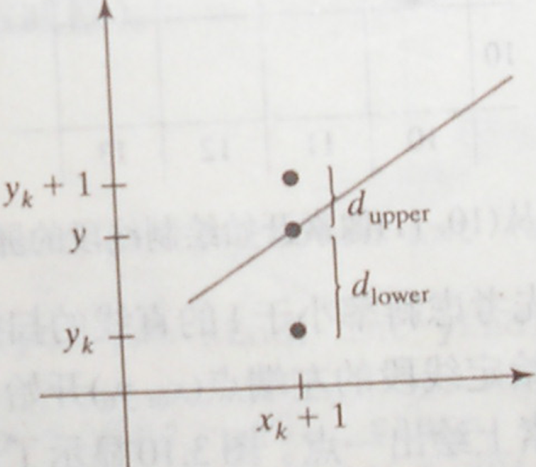
算法步骤:
假设$d{lower} < d{upper}$,则说明当前节点离下面的后继近,因此选择下面的节点。反之选择上面的节点
决策函数:
如果$pk$ < 0则 $y{k+1} = yk$,否则$y{k+1} = y_k + 1$
其中 $y{k+1} - y_k$ = 0或1. 需要注意的是$P_i$是第$x{k+1}$个点的。也就是说$p0$是计算第二个点的归属地,因此第三个点的$y{k+1} - yk$实际上是y1 - y0.也就是说如果$p_k < 0$,则$p{k+1}$的$y_{k+1} - y_k = 0$
实现:
1 | |
圆生成
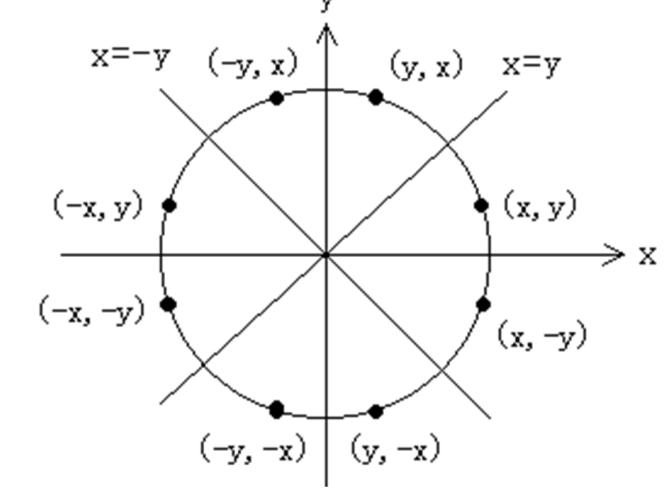
如图所示,我们可以把圆分成8个对称的部分,此时我们只需要求1/8然后利用对称映射到其他位置即可。而我们一般求解(y,x)对应的曲线
中点画圆算法
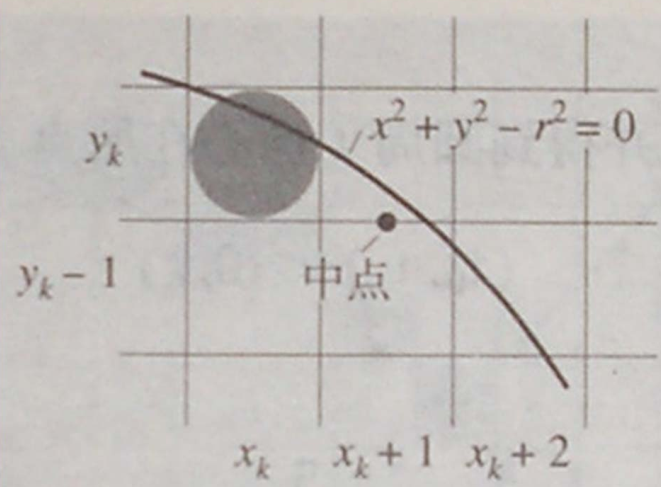
如图所示,假设我们已经求解了第k个点,第k+1个点的纵坐标只可能是$yk$或$y{k}-1$.因此我们需要想方法判断下一个点纵坐标位置。
过程:
两个代选点的中点坐标为($x_k + 1, y_k - \frac{1}{2}$).
将中点坐标代入上述方程,如果小于0表示该点在圆内,则曲线经过上面一个点,因此$y{k+1} = y_k$,反之$y{k+1} = y_k - 1$.
同样 $y_{k+1} = y_k 或 y_k - 1$
$p0 = f{circ}(1, r - 1/2) = 5/4 - r(如果是整数取1-r)$

贝塞尔曲线
公式:
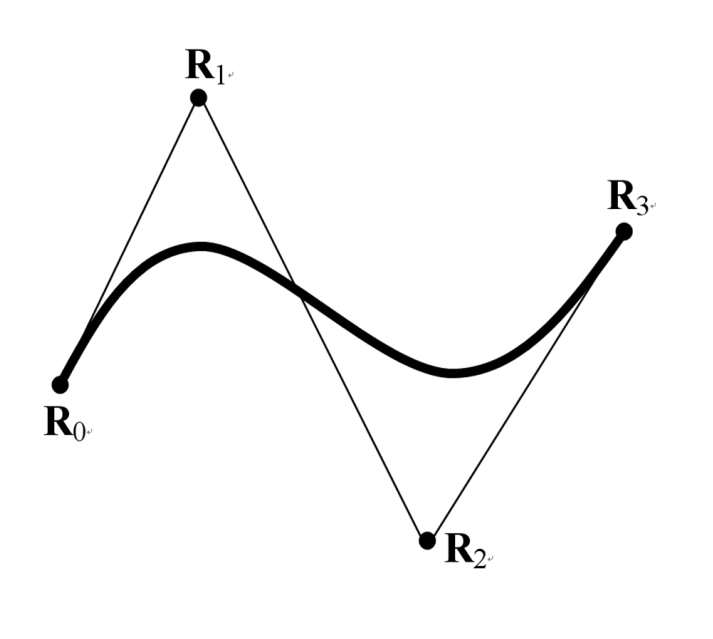
上面的式子就是贝塞尔曲线的表达式,其中$P_i$是第i个控制点。下面图中的点就是控制点。
它的优点在于他同样只需要改变t就可以绘制出整个图形并且可以通过改变点的坐标改变曲率
三次贝塞尔曲线的展开式为:
性质:
- 端点插值: 即 $R(0) = R_0 R(1) = R_n$. 通过这个性质我们很容易把两条贝塞尔曲线拼接起来,因为起点就是第一个点,终点是最后一个点。
端点切向: $R^{‘}(0) = n(R1 - R_0 ) \quad R^{‘}(1) = n(R_n - R{n-1})$.这条性质的含义为起点的斜率为R1R0的斜率,终点的斜率为RnRn-1的斜率。
利用这条性质可以让两条曲线的拼接处变得平滑,只需要两个拼接处点的斜率相同即可
- 对称性: $\sumi R{n-i}B{i,n}(t) = \sum_i R_i B{i, n}(t)$.例如: $R_0 B(0, 3) + R_1 B(1, 3) + R_2 B(2, 3) + R_3 B(3, 3) = R_3 B(0, 3) + R_2 B(1, 3) + R_1 B(2, 3) + R_0 B(3, 3)$。这是从头到尾的翻转,而不能是其中一两个置换。例如R0 R2 R1 R3则不等于R0 R1 R2 R3
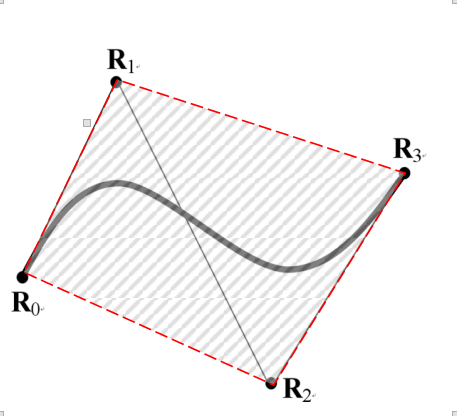
- 凸包性: 贝塞尔曲线位于控制点围成的多边形内。利用这个性质可以限制贝塞尔曲线的范围,防止他超界
- 几何不变性: 它仅和控制多边形有关,和坐标系无关
线的填充
逐点判断算法
逐点判断算法方法是判断每一点是否在多边形内,如果是则填充。
判断一点在多边形内部算法:
从该点水平向右发出一条射线,如果和多边形相交奇数次,则说明在外部,否则在多边形内部。
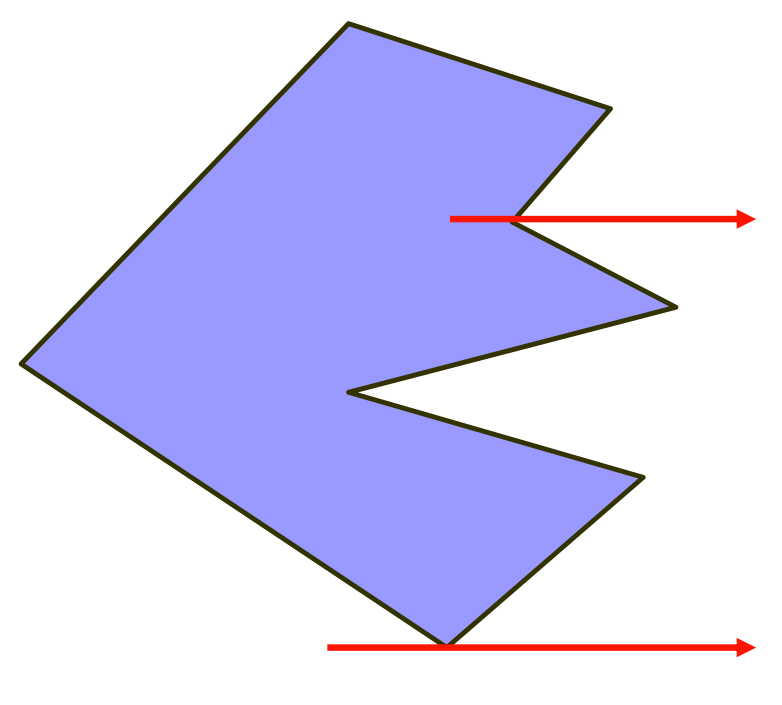
如图是两种特殊情况,在和两条边交界处判断到底是算一个点还是算两个点。
如果该点对应两条边的纵坐标一个比交点大,一个比交点小,那么只算一个点,如图中上面一条线。
如果两条边纵坐标都比该交点大或者都比该交点小,那么算两个点,如图中下面一条线。
扫描线算法
上面一种算法毫无疑问非常慢,在实践中不可能使用。扫描线算法利用到区域连贯性,速度大为提升。
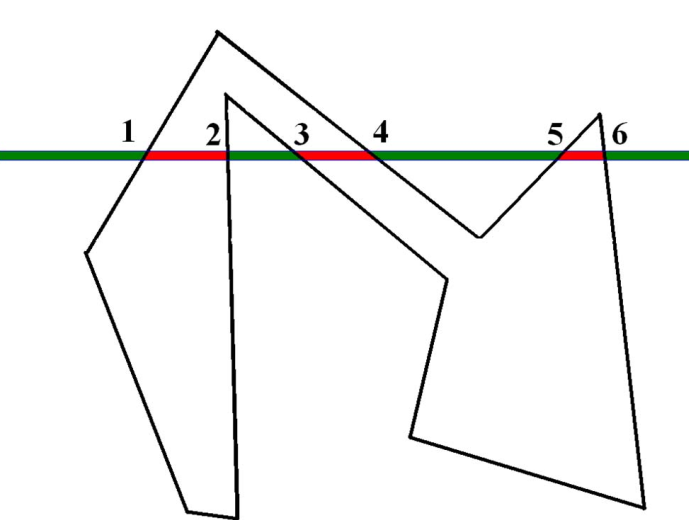
如图12是一个绘制区域,34,56分别也是一个绘制区域,可以看出来发出一条射线连续的两个相交点之间的区域是可填充的,并且这里的一些特殊点的规则和上面相同。
根据这个规律可以进行一些简化。
此外相邻扫描线(y1 = y2 + 1) 在多边形同一条边上也有一些规律。
也就是说求得扫描线和边的交点之后,可以通过上述算法快速的得出下一个相交点的位置。
算法过程:
- 计算y = $y_{min}$和多边形的交点
- 将y的值加1,并且按照上面的式子计算交点序列
- 判断位于多边形内部的区段并着色
为了实现上述算法,还需要两个数据结构,边表(ET)和活化边链表(AEL)
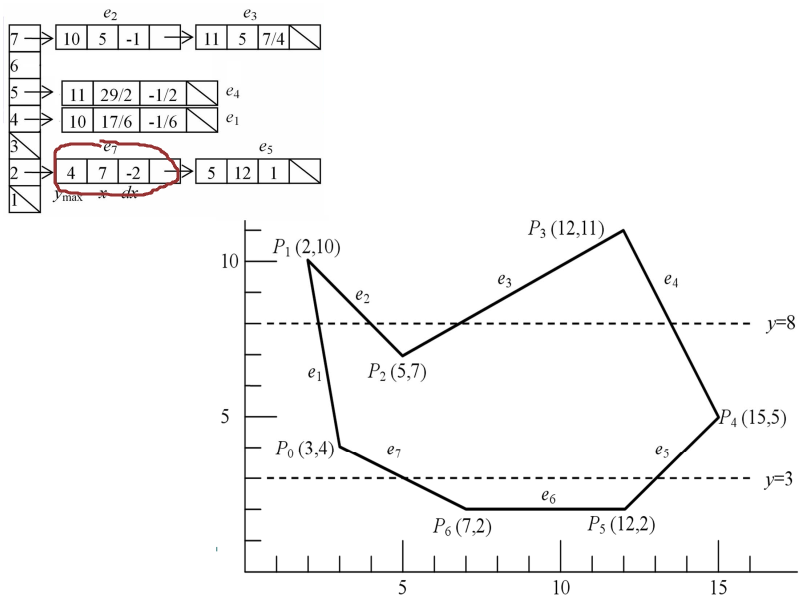
如图所示是边表的结构,其中数组的值是边的纵坐标最小值,而每个节点中记录了边的纵坐标最小值,下端点的x坐标和边斜率的倒数。
例如2位置e7边,纵坐标最小值为2,因此他在2位置。纵坐标最大值是4,下端点x坐标是7,斜率倒数是-2.
水平边不加入边链表,其次纵坐标相同的边是从左到右排布的
活化边链表代表着当前扫描时有效的边.
例如y=3时有效的边为e7,e5,因此边链表为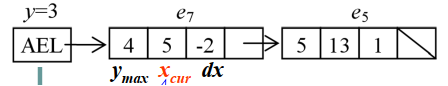
有了这两个数据结构,现在就能详细描述过程了
- 初始化两个表
- 如果此时扫描线y = $y_0$,并且ET中该位置非空,则加入到AEL中,并且将其从ET中删除。AEL中的边按照x值进行排序
- 如果活化链表非空,则将边两两配对,然后对这些边进行着色
- 将满足y = $y_{max}$的边从AEL中删除
- 然后对每条边x += dx
- y = y+1
线的裁剪
二维线裁剪:
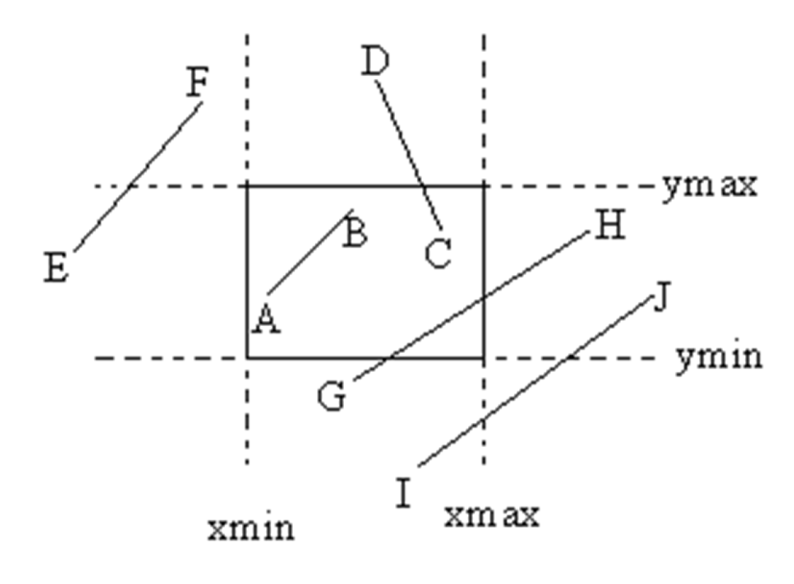
如图,需要将这些线限制在矩形区域内。线和窗口的关系有:
- 全部在矩形内
- 部分在矩形内
- 全部不在矩形内
Cohen-Sutherland算法
该算法可以加速对不在矩形区域内的判别,并且可以直接推广到三维。
他将平面分成9个区域,每个区域编码为$C_t C_b C_r C_l$.
C_t(top)的含义是纵坐标比上边界大则为1,反之则为0,其他含义类似。
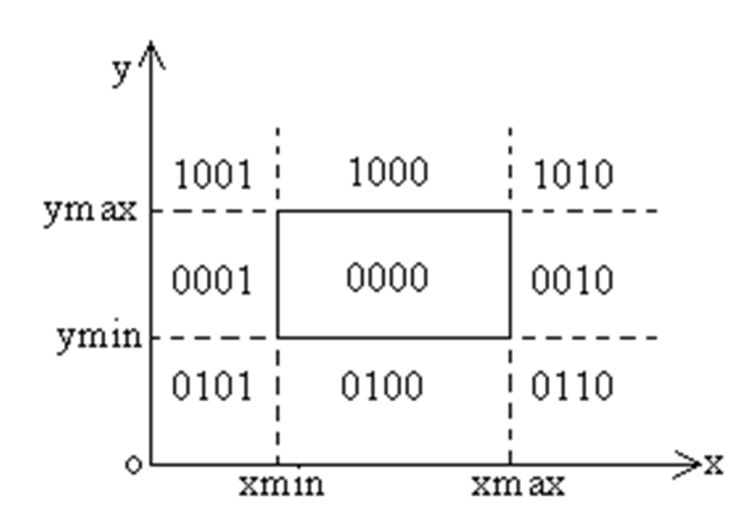
可以使用这个编码判断是否该线段是否完全不在窗口内。判断方法为 两个点的编码相与结果不为0.
例如
计算过程:
- 判断是否完全在窗口内(两点都在窗口内),如果不是则进入第二步
- 判断是否完全不在窗口内,如果不是则进入第三步
- 求线段和边界的交点,将在窗口外的一段抛弃,然后剩下一段重新进行判断。
交点计算方法:
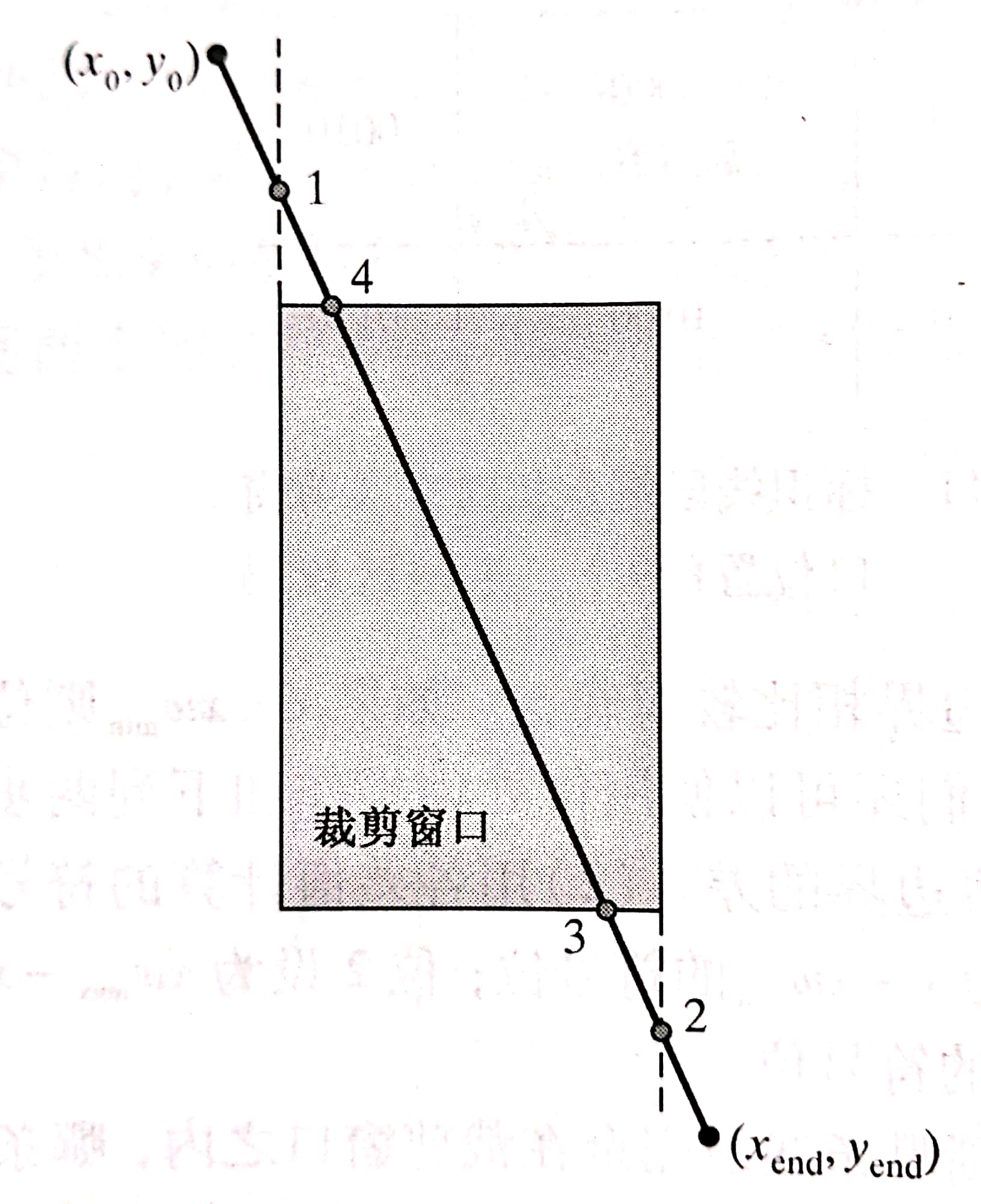
假设线段的两个端点 P1(x0, y0) P2(xend, yend),则线段的方程为:
左边界方程 x = $x_{min}$
于是和左边界坐标为($x{min}$, $y_0 + m(x{min} - x0 )$).也就是1点。同时我们判断 code1 & 0b0001 != 0,也就表示该点在窗口左边,因此可以截取左边这一部分,因此现在截取线段为$P_1 P{end}$
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56while(!done)
{
code1 = encode(p1);
code2 = encode(p2);
if(accept(code1, code2))//如果两个点都在内部,直接结束
{
done = true;
plotLine = true;
}
else
{
if(reject(code1, code2))//如果两个点都在外部,同样结束
{
done = true;
}
else
{
if(inside(code1))
{
swapPts(&p1, &p2);//交换两个点,只有在外面的点才会被舍弃
swapCodes(&code1, &code2);
}
if(p2.x != p1.x)
{
m = (p2.y - p1.y) / (p2.x - p1.x);
}
if(code1 & winLeftBitCode)//winLeftBitCode也就是0b0001
{
p1.y += (winMin.x - p1.x) * m;
p1.x = winMin.x;
}
else
{
if(code1 & winRightBitCode)
{
p1.y += (winMax.x - p1.x) * m;
p1.x = winMax.x;
}
else
{
if(code1 & winBottomBitCode)
{
...
else
{
if(code1 & winTopBitCode)
{
...
}
}
}
}
}
}
}
Nicholl-Lee-Nicholl算法
它只适用于二维,不适用于三维
步骤:
- 将区域分成九个部分,判断点在哪个部分
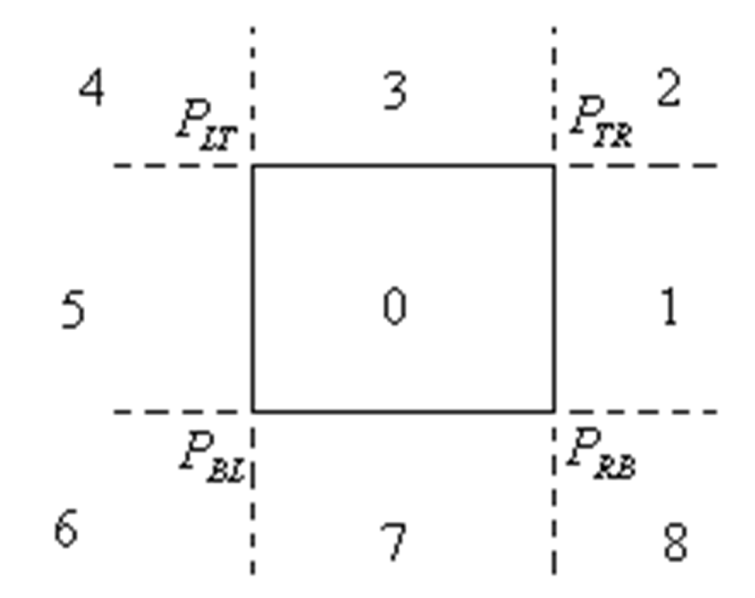
- 从起始点向窗口四个角点发出射线,共有如图四种情况
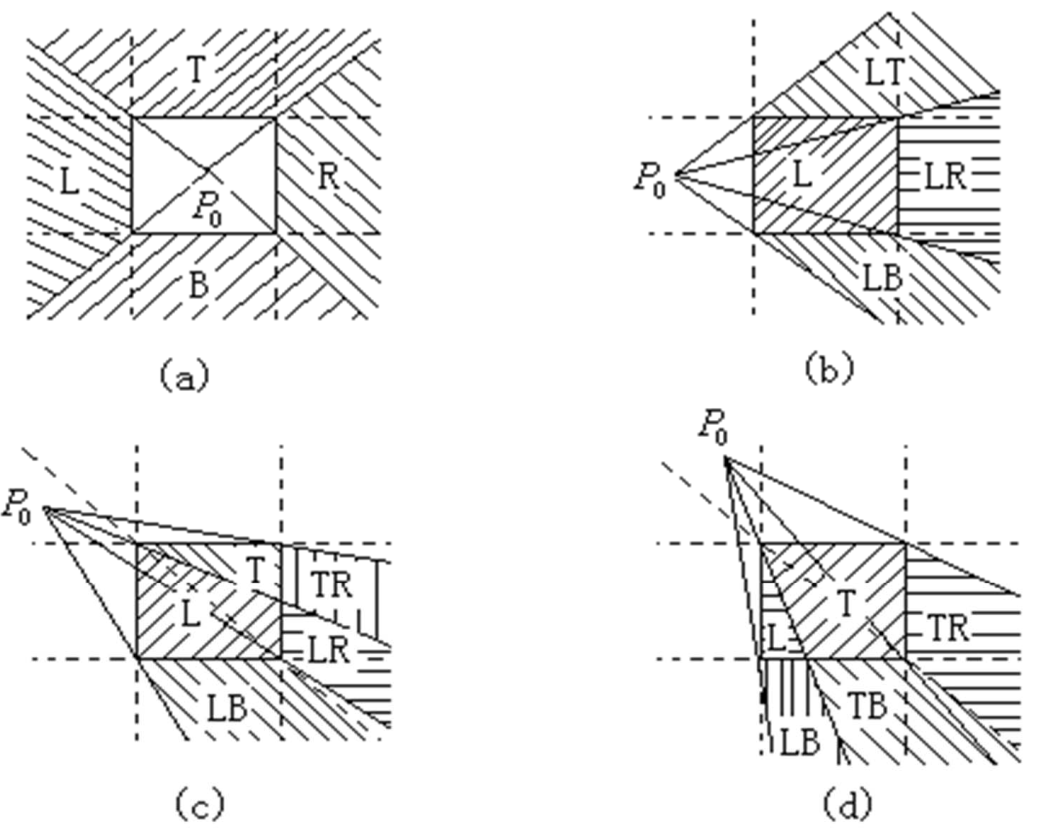
- 确定终点所在区域。可以通过斜率大小进行判断。这样可以快速确定他和哪些面相交。
- 求出交点
梁友栋-Barsky算法
直线的参数形式:
直线在裁剪窗口内条件:
改写得:
写成 $u p_k \le q_k$的形式可得:

如图所示从矩形外部进入矩形内部称为外部到内部。具体到每一条边来看:
- 左边界: 从左边到右边称为外部到内部,也就是$p_1 < 0$($p_1 < 0,则 \Delta x > 0$)
- 右边界: 从右边到左边称为外部到内部,也就是$p_2 < 0 $
- 下边界: 从下面到上面称为外部到内部, $p_3 < 0$
- 上边界: 从上面到下面称为外部到内部,$p_4 < 0$
算法过程:
- 当$p_k = 0$时,如果$q_k < 0$,则线段全在边界外,舍弃。$p_k = 0$表示$\Delta x 或 \Delta y$ = 0,也就是平行于x轴或y轴。只要$q_k < 0$这个式子就一定不成立。只要四个
- 根据上面判断可知$p_k < 0$时从外部到内部, $p_k > 0$时从内部到外部.然后和延长线相交一定会有两个出点,两个入点,找到这四个点对应的u = $\frac{q_k}{p_k}$
- $pk < 0$的点和0归为一类(入点), $p_k > 0$和1归为一类(出点),找出点的最大值,找入点的最小值。
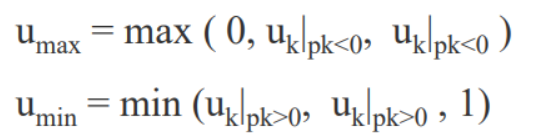 而$u{max} 和 u{min}$就是我们找的裁剪线段的两个端点,如果$u{max} > u_{min}$则完全落在窗口之外,舍弃。
而$u{max} 和 u{min}$就是我们找的裁剪线段的两个端点,如果$u{max} > u_{min}$则完全落在窗口之外,舍弃。
计算步骤:
- 计算$\Delta x \quad \Delta y$
- 计算$p_k \quad q_k \quad u_k$
- 计算$u{max} u{min}$
- 根据$u_{max} u{min}$得出最终线段
多边形裁剪
多边形裁剪和线段裁剪最大的不同是需要考虑裁剪区域的问题。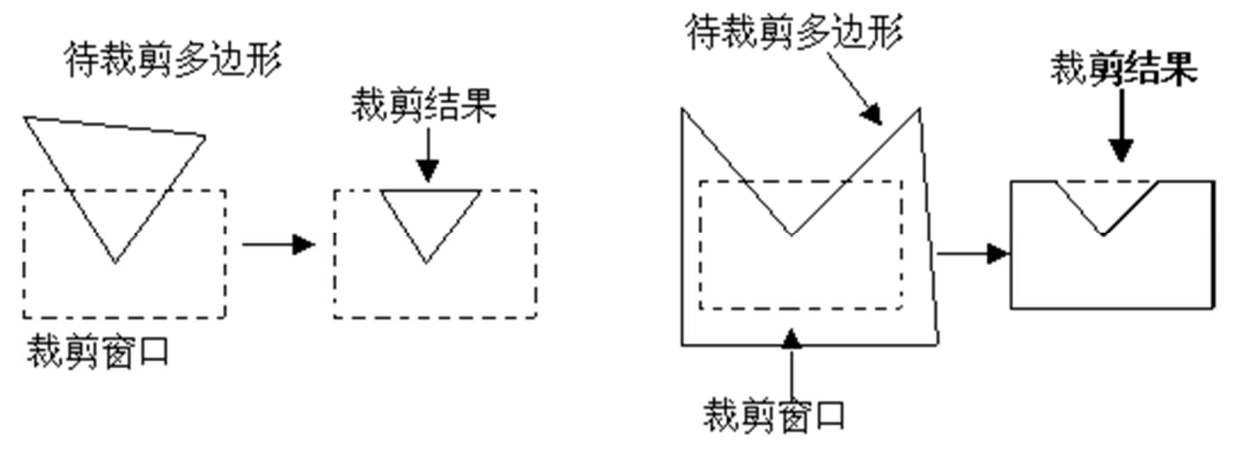
Sutherland-Hodgman算法
算法过程:
- 裁剪左边界。首先将多边形的边分为四种情况。
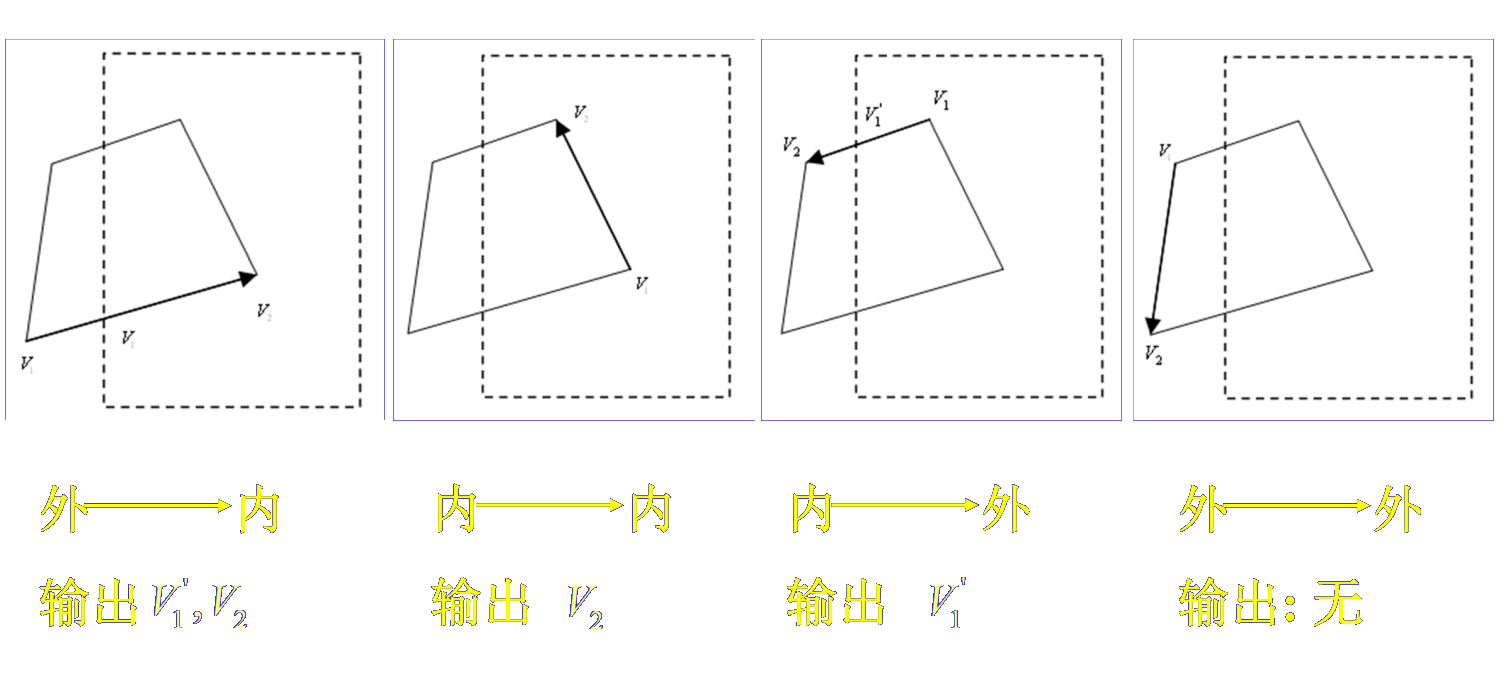
- 将获得的点首尾相连拼接成一个新的封闭图形
- 之后分别裁剪右边界,下边界,上边界
例如: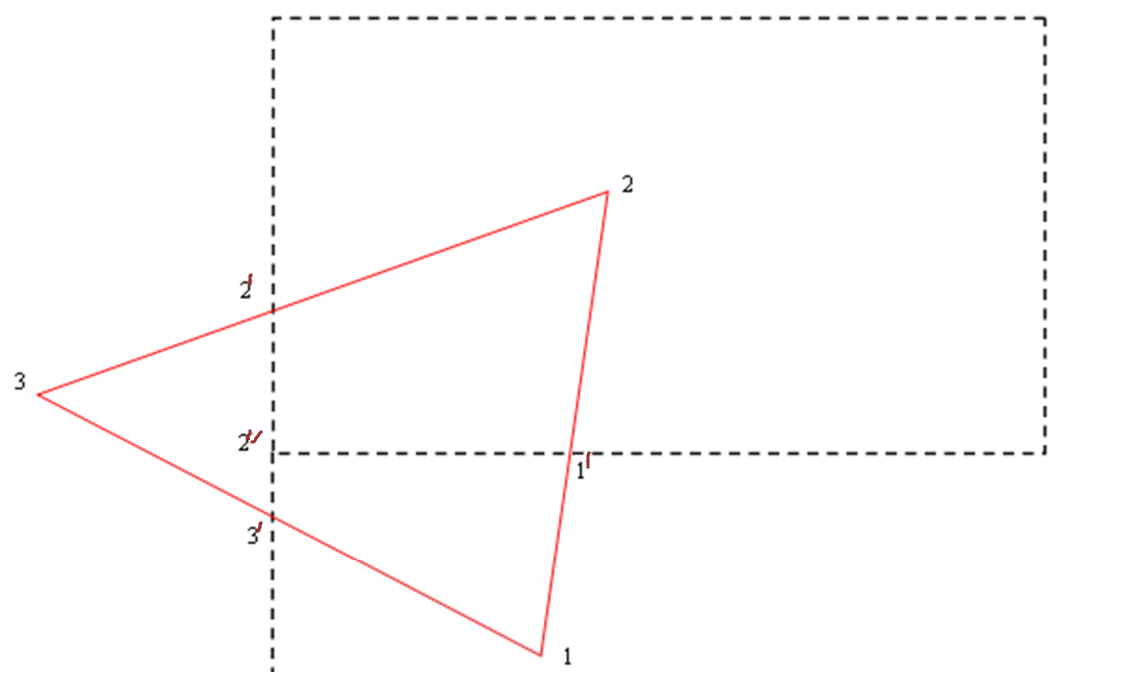
现在需要将他裁剪
过程:
裁剪左边界:
- 12边全在内侧(左边界的右边是内侧),因此保留2点
- 23边由内到外,保留$2^’$点
- 31边右外到内,保留$3^’$和1点
- 剪切可获得1, 2, $2^’$, $3^’$四个点,形成了12, 2$2^’$, $2^’ 3^’$, $3^’$1四条边做成封闭图形。
裁剪左边界完成后的图形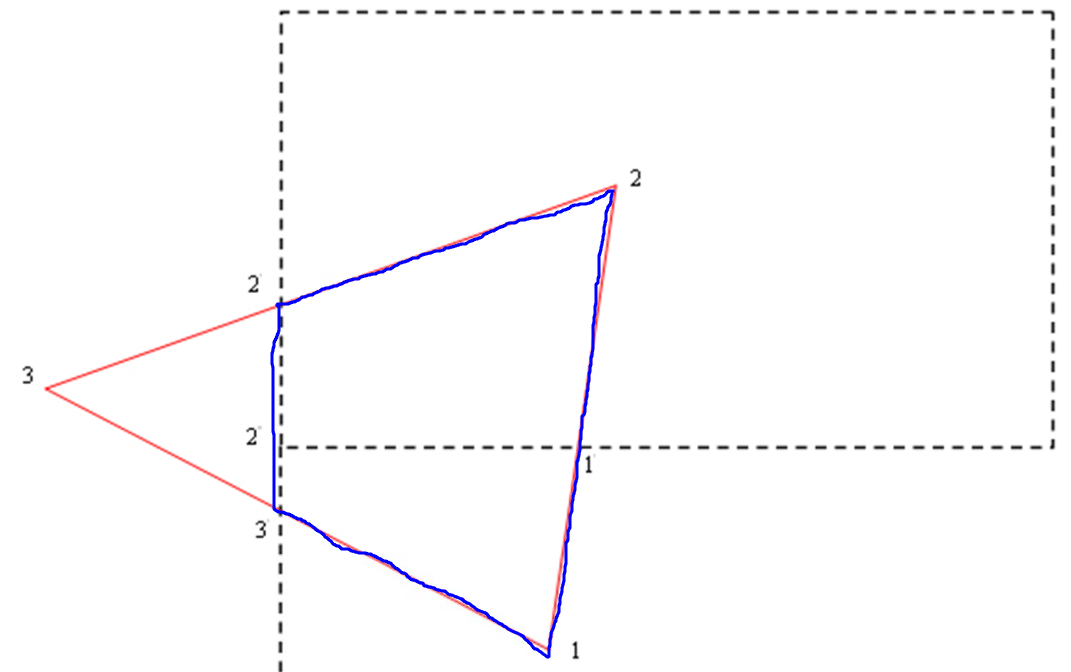
之后分别裁剪右边界,下边界,上边界,就将她限制在矩形区域内。
可以看到它的基本思想是将出边界的线全部截断。
它的裁剪窗口可以推广到凸多边形,但是对于被裁剪图形为凹多边形的情况下可能会有多余的线。
1 | |
Weiler-Atherton算法
它是一个更加通用的算法,它的裁剪窗口可以是任意多边形,并且被裁剪图形也可以是任意多边形。
概念:
多边形区域在线段左边
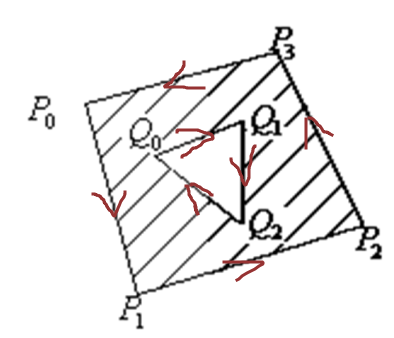
如图,对于外围边界来说左边就是逆时针旋转,但是对于内侧线段左边就是顺时针了
- 进点: 被裁剪多边形的边从外部进入裁剪多边形,相交点就是进点。
- 出点: 和进点相反
算法过程:
- 让多边形区域以逆时针的顺序遍历每一条边,直到碰到出点
- 碰到出点之后沿着多边形逆时针到达另一个相交点,如果该点对应边已经处理过了,那么走向下一步,否则如果该点是出点,则继续沿着多边形,如果是进点沿着被裁剪多边形的边走。
- 根据上面走过的边形成一个封闭图形
- 回到出点逆时针沿着边走(这时不需要沿着裁剪多边形的边了,因为处理过了)
例如:

如图,假设初始边为12
- 12有个出点,沿着裁剪多边形边走
- 走到61有个入点,沿着被裁剪多边形走
- 回到1点,已经走过,因此获得第一个封闭图形
- 再从12的出点沿着被裁剪多边形走
- 走到45有个入点还是沿着被裁剪多边形走
- 走到56有个出点,沿着边走
- 碰到了45边已经走过,因此获得了第二个封闭图形
- 再从45的出点往被裁剪多边形的边走
- 走到61边结束
面的表示
面的表示借用了线的表示的思想,它的表达式为
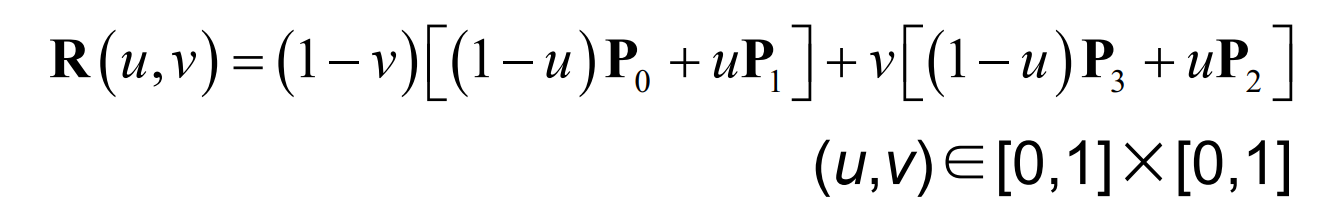
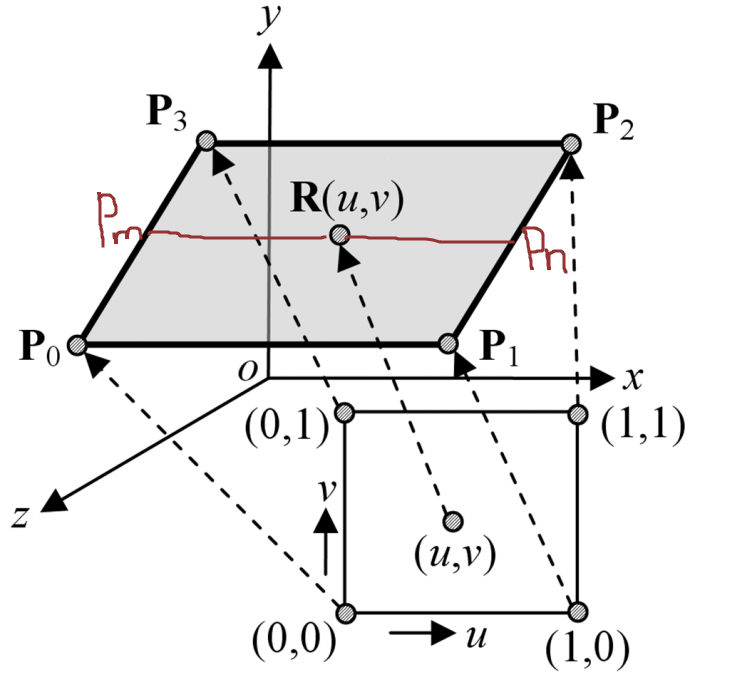
它同样是进行投影操作,计算过程为:
- 假设v不变,那么$P_m = vP_0 + (1-v) P_3$, $P_n = vP_1 + (1-v) P_2$
- 根据$P_m$和$P_n$可以求得R = $(1-u) P_m + u P_n$