本文最后更新于 2024年10月1日 上午
介绍
后缀中的后缀是一个字符串的所有后缀。例如abcde的后缀有5个,分别是abcde,bcde,cde,de,e。
后缀树是一种字符串算法,它可以被用于字符串搜索,寻找最长公共子串,查找匹配次数等。常见的匹配算法如KMP算法都是在模式串上做文章,而后缀树确实在匹配串上构建的。
后缀树需要满足五条性质:
- 如果字符串长度为n,那么后缀树中有n个叶子
- 除了根节点,所有除叶结点外的节点都至少有两个儿子
- 每条边上都标有非空子串S
- 没有同一个点延伸出的两条边上标记的字符串首字母相同
- 从根节点拼接每条边的子串到叶结点便可以获得一个后缀
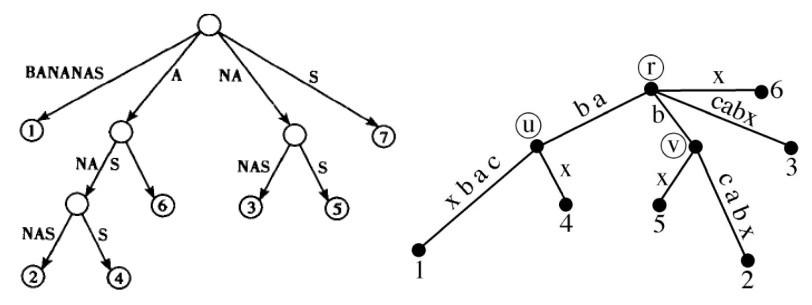
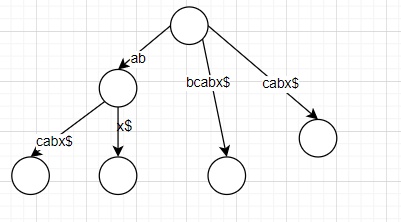
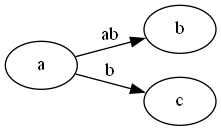
如图左边是BANANAS的后缀树,右边abcabx的后缀树。
是否存在abcab的后缀树呢?
答案是不存在,因为现在ab的后缀是abcab的前缀,也就是说现在想要满足条件4那么原来连接叶子节点4的边中子串要由x变成空串,但是这又违反了规则3.
为了避免上述问题,可以在字符串后面加上一个不在字符集中的字符$
应用
- 查询字符串是否是某一字符串的子串: 使用后缀树进行匹配,如果匹配串所有字符匹配成功则为子串
- 查询是否为后缀: 如果匹配到叶子节点正好匹配结束则为后缀
- 查询字符串出现次数: 匹配完成后子树的叶子数量
- 查找最长重复: 找到最深的至少含有两个叶子的节点
构建
brute-force 算法
这是一种暴力算法,复杂度为O($n^2$)。
算法过程:
- 假设构建字符串S的后缀树,定义S[0]为S本身,S[1]为长度S-1的后缀
- 初始化一个叶子节点,它和根节点之间的边为字符串S
- 将S[1]和边进行匹配,当匹配到不相同否就进行分叉
- 用S[2], S[3],…重复第二步直到所有后缀匹配完成
例:
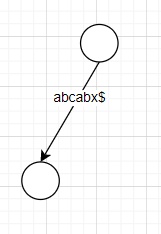
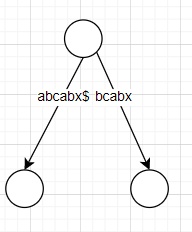
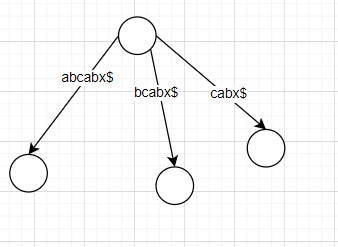
ukk算法
ukk算法的复杂度为O(n)。它是一种online算法。
下面参考了这篇文章
简单例子
首先尝试构建abc的一个后缀树。
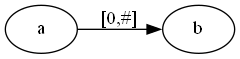
其中#可以认为是当前构建的末尾,第一步中#在a的右侧,即a#bc,因此[0,#]可以认为是a
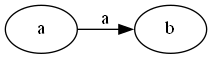
第二步让#右移一位,变成:
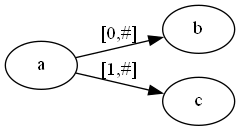
第三步再右移一位:
这样我们成功构建出一棵后缀树
详细例子
现在我们来构建一个复杂字符串abcabxabcd的后缀树
首先给出一些概念:
- 活动点: 是一个三元组,包括(active_node, active_edge, active_length).
- 剩余后缀数: 代表还需要插入多少个新后缀
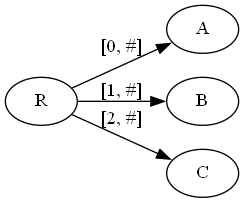
构建该字符串后缀树时前三个字符构建和上面例子相同,现在处理第四个字符a.
此时活动点为(R, 空, 0),剩余后缀树为0,也就是说我们每次需要插入的新后缀数为1,即最后一个字符。
插入完成后为:
- 活动点为(R, a, 1),他表示当前活动点是根节点,并且活动边是从根节点开始,并且首字符是a的边,1表示分支位置是活动边上的第一个字符
- 剩余后缀数是1, 表示当前还有一个后缀需要插入
状态为#=4, (R, a, 1), 1
图和上一步一样 即
即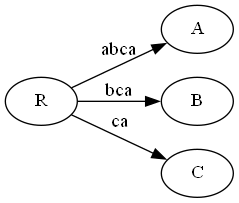
第五步处理b,此时沿着活动节点匹配发现a后面正好是b,因此不需要修改图,只需要处理活动节点和剩余后缀数.
#=5, (R, a, 2), 2
第六步处理x,此时沿着活动节点匹配下一个字符应该是c,但此时是x,因此需要进行处理,此时共有abx,bx,x三个后缀。此时状态为#=6, (R, a, 2), 3
首先处理a, b, x,因为我们根据第五步的活动节点已经知道了ab的位置,因此我们只需要分裂ab再添加一个新的后缀即可
digraph ukk{
rankdir=LR;
R -> A [label="bcabx"];
R -> B [label="cabx"];
R -> C [label="ab" color=blue];
C -> D [label="cabx" color=blue];
C -> E [label="x" color=blue];
}
处理完成之后新的活动点变成了#=6, (R, b, 1), 2。由此我们可以归约出规则1
当向根节点插入时遵循:
- active_node为root
- active_edge为即将被插入的新后缀首字符
- active_length减1
然后现在由于b后面接的是c,而我们现在要插入的后缀是bx,因此仍然需要分裂
digraph ukk{
rankdir=LR;
R -> A [label="b" color=blue];
A -> F [label="cabx" color=blue];
A -> G [label="x" color=blue];
R -> B [label="cabx"];
R -> C [label="ab"];
C -> D [label="cabx"];
C -> E [label="x"];
}
更新后活动点变成了(R, x, 0), 1。但是此时并没有更新完成,这里涉及到规则2
如果分裂一条边并且插入一个新的节点,如果该节点不是当前步骤创建的第一个节点,则前一个插入的节点和新节点通过一个特殊的指针连接,称为后缀连接,通过虚线表示
因此本次更新真正的图像是
digraph ukk{
rankdir=LR;
R -> B [label="cabx"];
R -> A [label="b" color=blue];
A -> F [label="cabx" color=blue];
A -> G [label="x" color=blue];
R -> C [label="ab"];
C -> D [label="cabx"];
C -> E [label="x"];
C -> A [style="dotted"];
}
然后处理新的活动点,由于原来的边中没有x开头的字符串,因此直接加入即可
digraph ukk{
rankdir=LR;
R -> B [label="cabx"];
R -> A [label="b" color=blue];
A -> F [label="cabx" color=blue];
A -> G [label="x" color=blue];
R -> C [label="ab"];
C -> D [label="cabx"];
C -> E [label="x"];
C -> A [style="dotted"];
R -> H [label="x"]
}
因此我们可以总结出活动点为根节点时的规则
> 如果active_edge为空则查找根节点下的所有边,如果首字符和当前字符相同,则active_edge为当前字符,active_length为1,否则直接插入。
> 如果active_edge不为空,则判断active_edge下active_length位置的字符是否相同,如果相同active_length++,如果不同则使用上面两条规则进行分裂
继续第7步(字符为a)`#=7, (R, a, 1), 1`和第8步(字符为b)`#=8, (R, a, 2), 2`
处理第9步,字符为c。注意此时active_node变成了节点C。`#=9, (C, c, 1), 3`
处理第十步,字符为d。此时由于没有匹配需要进行分裂,并且此时剩余后缀数为4也就是说需要处理abcd,bcd,cd,d四个后缀。
digraph ukk{
rankdir=LR;
C [color=red];
R -> B [label="cabxabcd"];
R -> A [label="b" ];
A -> F [label="cabxabcd"];
A -> G [label="xabcd"];
R -> C [label="ab"];
C -> D [label="c" color=blue];
D -> I [label="d" color=blue];
D -> J [label="abxabcd" color=blue];
C -> E [label="xabcd"];
C -> A [style="dotted"];
R -> H [label="xabcd"]
}
此时状态转移涉及到规则3
当active_node不是root时,我们沿后缀连接寻找节点,如果存在,那么设置后缀连接的节点为active_node。如果不存在,则设置active_node为root。active_edge和active_length保存不变
根据规则3,进行完上图的变换后活动点为(A, c, 1),此时剩余后缀数为3。然后下一个要处理的后缀为bcd,此时C节点下有一条边的首字符也是c,和活动点的active_edge对应,因此图为
digraph ukk{
rankdir=LR;
A [color=red];
R -> B [label="cabxabcd"];
R -> A [label="b" ];
A -> F [label="c" color=blue];
F -> K [label="d" color=blue];
F -> L [label="abxabcd" color=blue];
A -> G [label="xabcd"];
R -> C [label="ab"];
C -> D [label="c"];
D -> I [label="d"];
D -> J [label="abxabcd"];
C -> E [label="xabcd"];
C -> A [style="dotted"];
R -> H [label="xabcd"];
D -> F [style="dotted"];
}
根据规则2,本次处理完成后还要加上后缀连接。
从中我们可以看到,后缀连接可以让我们快速的重置活动点。例如,C的边为ab,而A的边为b,因此正好处理完C后跳转到A。D和F同理。
由于A没有后缀连接,因此现在状态为(R, c, 1),剩余后缀数为2,要处理的后缀为cd。
digraph ukk{
rankdir=LR;
R [color=red];
R -> B [label="c" color=blue];
B -> M [label="d" color=blue];
B -> N [label="abxabcd" color=blue];
R -> A [label="b" ];
A -> F [label="c"];
F -> K [label="d"];
F -> L [label="abxabcd"];
A -> G [label="xabcd"];
R -> C [label="ab"];
C -> D [label="c"];
D -> I [label="d"];
D -> J [label="abxabcd"];
C -> E [label="xabcd"];
C -> A [style="dotted"];
R -> H [label="xabcd"];
D -> F [style="dotted"];
F -> B [style="dotted"];
}
然后根据规则1活动点变为(R, d, 0),也就是说只要插入一条新的边
digraph ukk{
rankdir=LR;
R [color=red];
R -> B [label="c"];
B -> M [label="d"];
B -> N [label="abxabcd"];
R -> A [label="b" ];
A -> F [label="c"];
F -> K [label="d"];
F -> L [label="abxabcd"];
A -> G [label="xabcd"];
R -> C [label="ab"];
C -> D [label="c"];
D -> I [label="d"];
D -> J [label="abxabcd"];
C -> E [label="xabcd"];
C -> A [style="dotted"];
R -> H [label="xabcd"];
D -> F [style="dotted"];
F -> B [style="dotted"];
R -> O [label="d"];
}





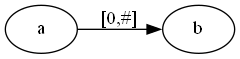





 即
即