字符串之KMP算法
由（扯）来（蛋）
Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP 算法”，常用于在一个文本串 S 内查找一个模式串 P 的出现位置，这个算法由 Donald Knuth、Vaughan Pratt、James H. Morris 三人于 1977 年联合发表，故取这三人的姓氏命名此算法。
最长前缀和与后缀和
例如给出一个字符串ABCDABD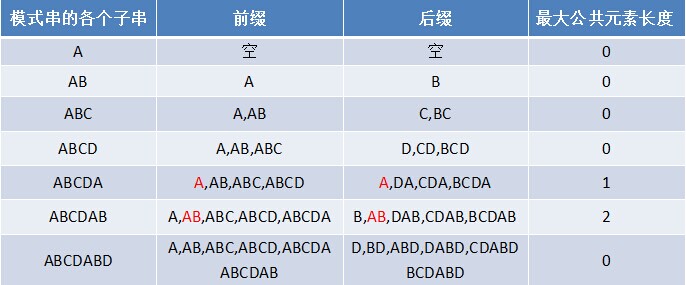
前缀和就是从前往后数i个，后缀和是从第n-i个数到最后一个，首先我们便要找到每一个字母的最长相同前缀后缀和，然后求next数组，注意，只有一个元素时是不计算前缀后缀的，直接看为0
next数组
next数组考虑的是除当前字符外的最长相同前缀后缀，实际上就是前一个前缀后缀和，因为把最后一个字母上去之后必定会使后缀和少一个，因此前缀后缀和也会-1，注意next数组中会出现-1，实际上这个数组就是将原数组整体右移一位，然后在第0位补上-1
用next数组进行匹配
匹配失配，j = next [j]，模式串向右移动的位数为：j - next[j]。换言之，当模式串的后缀 pj-k pj-k+1, …, pj-1 跟文本串 si-k si-k+1, …, si-1 匹配成功，但 pj 跟 si 匹配失败时，因为 next[j] = k，相当于在不包含 pj 的模式串中有最大长度为 k 的相同前缀后缀，即 p0 p1 …pk-1 = pj-k pj-k+1…pj-1，故令 j = next[j]，从而让模式串右移 j - next[j] 位，使得模式串的前缀 p0 p1, …, pk-1 对应着文本串 si-k si-k+1, …, si-1，而后让 pk 跟 si 继续匹配。如下图所示：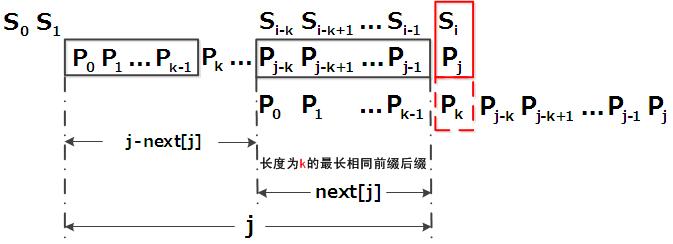
解释：因为前缀和后缀和相等，当最后一个匹配失误的时候就可以直接跳到后缀和开始的地方，这样就一下子匹配到了几位数，加快速度，至于合理性 ，K M P 这三个人已经证明过，而具体要跳几位呢？
比如说你有7个数，前面6个数已经匹配好了，结果第七位出了问题，这时一找next数组，发现第6位前缀和为2，那我们就要跳到第五位上去，找找规律，就是j-next[j]呀，没错，就是要跳这么多位，忘了自己推一下就好了，挺好推的
失配时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值
next数组求法
这里运用了递归的思想，首先对于前一两个可以直接写出来，然后对于后面的，假如第j个next值我们已经求出来了，那么对于第j+1个，
- 如果p[k]=p[j]，则next[j+1]=k+1
例如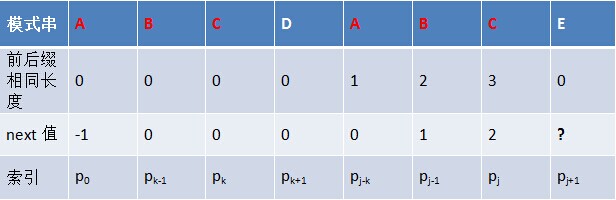
C为p[j]，E为p[j+1]，next[j]=2,则第一，第二个与第五，第六个相同，如果第三个和3七个相同，则最大相同长度就为3，即p[k]=p[j]
2.如果p[k]!=p[j],则递归找p[next[k]]是否等于p[j]，p[next[next[k]]]是否等于p[j],直到找到或到了开头
对于第二种情况，也可以通过图来展示
现在p[j]!=p[k]，那么肯定要缩小范围，我么已经知道第一个与第二个是匹配的了，那么第五个第六个对应与第一个第二个匹配，但如果那里面没有前后缀的话，你减去一个就相当于破坏了结构（前缀从前往后，后缀也是从前往后，减去一个便要求这这个前缀串里面前几个要和后缀串里面后面几个匹配，因此要求next[k]就是为了里面要匹配，这样只需比较p[next[k]]和p[j]即可），假如中间就碰到了，那么next[j+1]=next[next[k]]+1,如果没碰到，那么next[j+1]=0（一朝回到解放前）
代码实现：void GetNext(char* p,int next[])
{
int pLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < pLen - 1)
{
//p[k]表示前缀，p[j]表示后缀
if (k == -1 || p[j] == p[k])
{
++k;
++j;
next[j] = k;
}
else
{
k = next[k];
}
}
}
nextval
nextval是next的进阶版。例如某一位是next[5]，但是next[5]和5的字符相同，这样肯定还是不行，所以多比了一次。
nextval判断方法：在next的基础上,s是用来匹配的串
s[next[i]] = s[i], 继续比较。如果next[i]和next[next[i]]还是相同，那么要继续比，直到不相同或者过了第一个为止
s[next[i]] != s[i] , nextval[flag] = next[i]
匹配（最终代码）
匹配过程：
“假设现在文本串S匹配到 i 位置，模式串 P 匹配到 j 位置
如果 j = -1，或者当前字符匹配成功（即 S[i] == P[j]），都令 i++，j++，继续匹配下一个字符；
如果 j != -1，且当前字符匹配失败（即 S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串 P 相对于文本串 S 向右移动了 j - next [j] 位。
换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的 next 值，即移动的实际位数为：j - next[j]，且此值大于等于1。”
例 
例如此时i=10,j=6,此时文本串该位为空格，而匹配串为D，这时不匹配，就要让匹配串移动6-next[6]=4位，我令i=10,j=2,即匹配串为C,这就相当于让匹配位左移4位，而文本对应位不变，于是相当于匹配串右移4位（有种物理相对运动的既视感）
代码：int KmpSearch(char* s, char* p)
{
int i = 0;
int j = 0;
int sLen = strlen(s);
int pLen = strlen(p);
while (i < sLen && j < pLen)
{
//①如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++
if (j == -1 || s[i] == p[j])
{
i++;
j++;
}
else
{
//②如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]
//next[j]即为j所对应的next值
j = next[j];
}
}
if (j == pLen)
return i - j;
else
return -1;
}
感到了代码的优美感有没有！
但是这样还可以优化
//优化过后的next 数组求法 |
这里有点蒙，就先这样吧
