数值积分

基础概念

首先需要知道积分的含义： 在二重积分中，积分可以粗略的认为是求面积。由于我们是离散的点，因此常见的做法是使用矩形或梯形来逼近这块面积，如果采样点无限多，那么通过这种方法得出的结果就是精确的。

但是这种方法计算代价过大，我们可以利用这些点做插值来拟合曲线，再对插值函数进行积分得到更好的结果。

代数精度定义： 如果某个求积公式对于次数不超过m的多项式均能准确的成立，但对于m+1次的多项式不能准确的成立，则称该求积公式有m次的代数精度

这也就要求$\sum A_k = x^k$

也就是要求下式都成立

$$\left\{\begin{matrix} \sum A_k & = & b-a\\ \sum A_k x_k & = & \frac{1}{2}(b^2 - a^2 )\\ \vdots & &\\ \sum A_k x_k^m & = & \frac{1}{m+1} (b^{m+1} - a^{m+1}) \end{matrix}\right.$$

余项定义：

$$\begin{aligned} R[f] &= \int_a^b f(x) dx - \sum_{k=0}^{n}A_k x_k^{m+1} = Kf^{m+1}(\eta)\\ &当f(x) = x^{m+1}时，公式为\\ K &= \frac{1}{(m+1)!}[\int_a^b x^{m+1}dx - \sum_{k=0}^{n}A_k x_k^{m+1}]\\ &= \frac{1}{(m+1)!}[\frac{1}{m+2}(b^{m+2} - a^{m+2}) - \sum_{k=0}^n A_k x_k^{m+1}] \end{aligned}$$

如果求积公式中的$A_k$ > 0,则称该求积公式是稳定的

牛顿-科特斯公式

设将积分区间[a, b]划分成n等份, 步长为$h=\frac{b-a}{n}$, 选取等距节点$x_k = a + kh$构造出的插值型求积公式为

$$\begin{aligned} I_n &= (b-a)\sum_{k=0}^n C_k^{(n)}f(x_k )\\ C_k^{(n)} &= \frac{h}{b-a}\int_0^n \prod_{j=0 \&\& j\ne k}^{n} \frac{t-j}{k-j}dt\\ &= \frac{(-1)^{n-k}}{nk!(n-k)!} \int_0^n \prod_{j=0 \&\& j\ne k}^{n} t-j \, dt \end{aligned}$$

其实$C_k^{(n)}$就是拉格朗日插值的积分，积分内部就是拉格朗日插值的基函数

当n=1时，$C_0^{(1)} = C_1^{(1)} = \frac{1}{2}$。这也就是我们熟悉的梯形公式

当n=2时：

$$\begin{aligned} C_0^{(2)} &= \frac{1}{4} \int_0^2 (t-1)(t-2) dt = \frac{1}{6}\\ C_1^{(2)} &= -\frac{1}{2} \int_0^2 t(t-2) dt = \frac{4}{6}\\ C_2^{(2)} &= \frac{1}{4} \int_0^2 t(t-1) dt = \frac{1}{6} \end{aligned}$$

因此结果$S = \frac{b-a}{6} [f(a) + 4f(\frac{a+b}{2}) + f(b)]$。这就是辛普森公式

当n=4时称为科特斯公式，其形式为

$$C = \frac{b-a}{90} [7f(x_0 ) + 32f(x_1 ) + 12f(x_2 ) + 32f(x_3 ) + 7f(x_4 )]$$

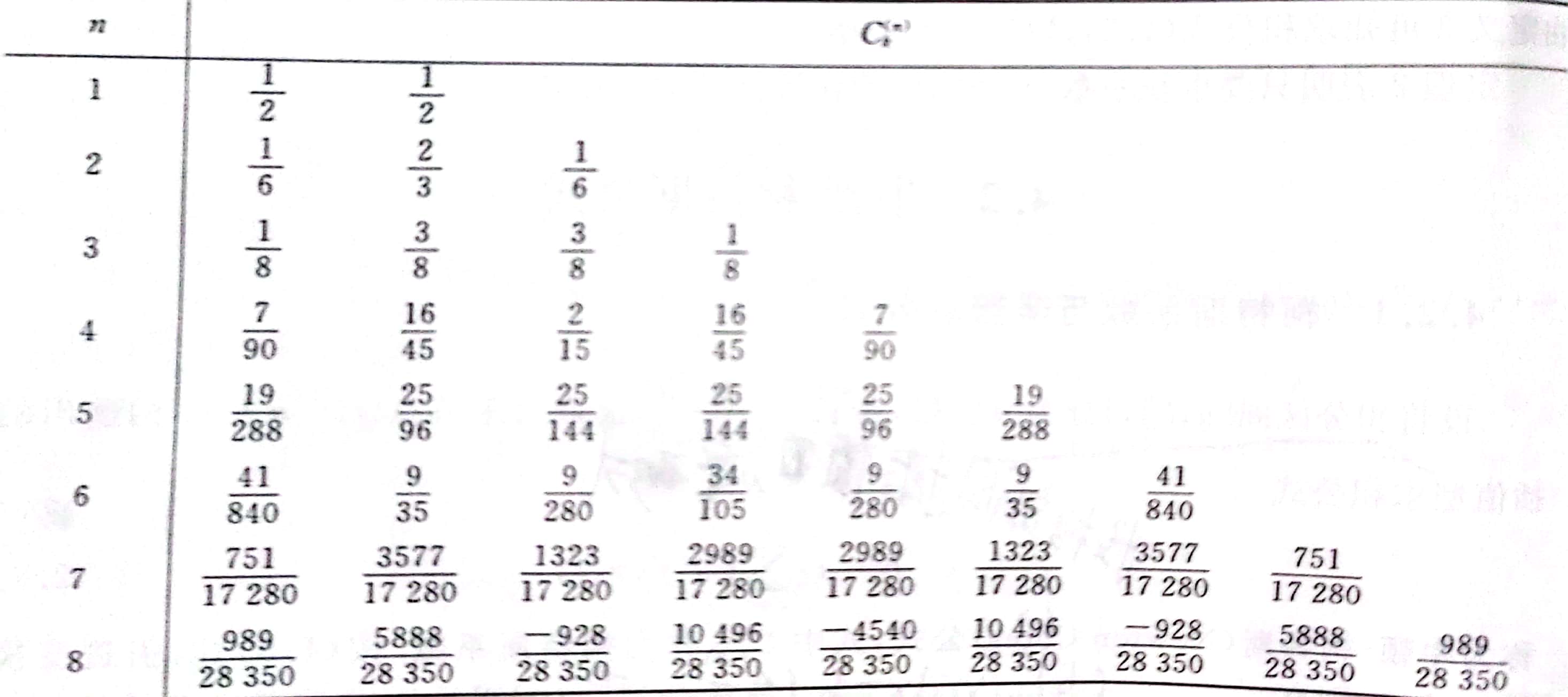
如图所示，当n=8时开始出现负数，这时候计算就是不稳定的，因此n$\ge$8时牛顿-科特斯公式是无法使用的

定理： 当阶n为偶数时，牛顿-科特斯公式至少有n+1次代数精度

也就是说n=2时有三次代数精度

复合求积公式

前面说的公式都只在区间上用两三个点，例如辛普森公式只用三个点就进行求解。实际使用时我们通常划分成若干个小区间，然后每个区间使用这些公式来保证精确度。

复合梯形公式

$$T_n = \frac{h}{2} \sum_{k=0}^{n-1} [f(x_k ) + f(x_{k+1})] = \frac{h}{2}[f(a) + 2\sum_{k=1}^{n-1}f(x_k ) + f(b)]$$

上式就是复合梯形公式，它的余项为

$$R_n (f) = I - T_n = \sum_{k=0}^{n-1} [-\frac{h^3}{12}f^{\prime \prime}(\eta_k)]=\frac{1}{2} [\frac{b-a}{n}\sum_{k=0}^{n-1}f(x_k ) + \frac{b-a}{n}\sum_{k=1}^{n}f(x_k )]$$

复合辛普森公式

$$S_n = \frac{h}{6}\sum_{k=0}^{n-1}[f(x_k )+4f(x_{(k+1)/2}) + f(x_{k+1})]\\ =\frac{h}{6} [f(a) + 4\sum_{k=0}^{n-1}f(x_{(k+1)/2}) + 2\sum_{k=1}^{n-1}f(x_k ) + f(b)]$$

龙贝格求积公式

龙贝格求积公式使用递推法实现了从梯形公式递推到辛普森公式到科斯特公式，也就是说计算过程中不断是复合的，并且还可以变步长，加快了收敛的速度。

梯形法的递推化

在[$xk , x{k+1}$]间加一个点$x{k+\frac{1}{2}} = \frac{1}{2} (x_k + x{k+1})$,使用复合梯形公式求得

$$\begin{aligned} T_{2n} &= \frac{h}{4}[f(x_k ) + 2f(x_{k+\frac{1}{2}}) + f(x_{k+1})]\\ &= \frac{h}{4}\sum_{k=0}^{n-1}[f(x_k ) + f(x_{k+1}) + \frac{h}{2}\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})]\\ &= \frac{1}{2}T_n + \frac{h}{2}\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}}) \end{aligned}$$

这样我们就找到了$T_{2n}和T_n$之间的递推公式，只需要计算中间点即可

误差为：

$$R_{2n} = I - T_{2n} = -\frac{b-a}{12}(\frac{b-a}{2n})^2 f^{\prime \prime}(\zeta_{2n})$$

党误差不大时，我们可以粗略的认为$f^{\prime \prime}(\zeta{2n}) \approx f^{\prime \prime}(\zeta{n})$,因此可以得到

$$\frac{I - T_{2n}}{I - T_n} \approx \frac{1}{4}$$

即$I-T{2n} = \frac{1}{3}(T{2n} - T_n )$

而$I-T{2n}$就是$T{2n}$的误差，因此我们把它补偿到原公式中可以让他更加精确，即

$$\bar{T} = T_{2n} + \frac{1}{3}(T_{2n} - T_n )$$

我们将$\bar{T}$展开就可以发现它就是辛普森公式，记为$S_{n}$

同理我们可以得到

$$\frac{I - S_{2n}}{I - S_n} = \frac{1}{16}$$

因此 $Cn = S{2n} + \frac{1}{15}(S_{2n} - S_n )$.$C_n$就是科特斯公式

龙贝格算法

龙贝格公式 其实就是$C_n$再进行一次递推得到的公式，它也就是n=6的牛顿-科特斯公式。之所以不再高是因为到n=8时牛顿-科特斯公式就不稳定

根据上面的递推形式，我们可以归纳成一个统一形式

$$T_m^{(k)} = \frac{4^m}{4^m - 1} T_{m-1}^{(k+1)} - \frac{1}{4^m - 1}T_{m-1}^{(k)}$$

其中m为加速次数，表示当前是梯形还是辛普森还是科特斯等。k表示当前计算精度的第几次计算。

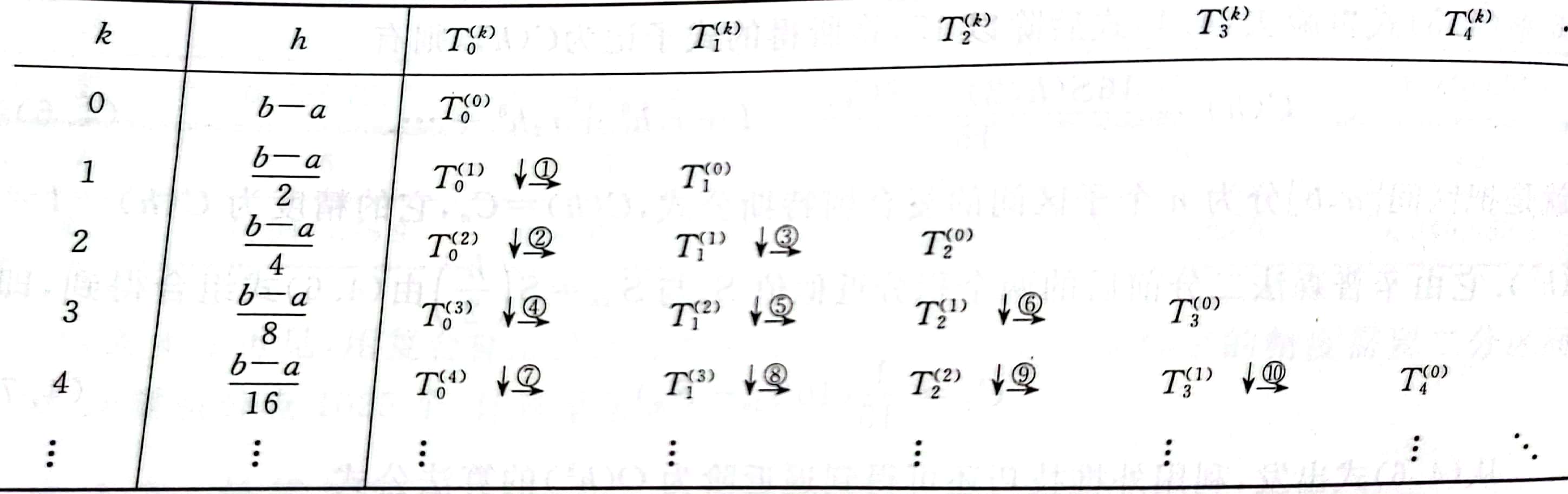
如图所示就是龙贝格算法的计算过程，最终只要算到$T_3^{(k)}$。如果$|T_3^{(k+1)} - |T_3^{(k)} < \varepsilon$则停止计算

自适应积分法

积分函数有时候一部分比较平缓，一部分比较陡峭，平缓的部分只需要少量的采样点，而陡峭的部分需要更多的采样点。为了达到这个目的提出了自适应积分法。

步骤：

1. 使用某种算法求整个区间的积分值s
2. 将区间进行二分，求两个区间积分值$s_1 \, s_2$并求和得$s_n$，如果$|s - s_n| < \varepsilon$,则停止该区间计算，否则对两个分区间进行上述过程
3. 所有区间都停止计算时结束

高斯求积公式

n+1个节点代数精度最高到2n+1次，但是前面所说的公式离这个目标差距甚远。高斯求积公式最高可以达到2n+1次

下面研究带权积分I = $\int_a^b f(x) \rho (x) dx$,$\rho(x)$为权函数，它的求积公式为

$$\int_a^b f(x) \rho (x) dx \approx \sum_{k=0}^{n} A_k f(x_k )$$

如果f(x) = $x^m$则有

$$\sum_{k=0}^n A_k x_k^m = \int_a^b x^m \rho (x) dx$$

要注意$A_k 和 x_k$都是未知数，因此总共有2n+2个未知量，因此代数精度最大为2n+1

定理： $a \le x_0 < x_1 < \dots < x_n \le b$是高斯点的充要条件是

$$\omega_{n+1}(x) = (x - x_0 )(x-x_1 )\dots (x- x_n )\\ \int_a^b p(x) \omega_{n+1}(x) \rho(x) dx = 0$$

其中p(x)是最高次数不超过x的多项式

证明

必要性： 如果$x0 , x_1 , \dots, x_n$是高斯点，则f(x) = $p(x) \omega{n+1}(x)$成立，则有

$$\int_a^b p(x) \omega_{n+1}(x)\rho(x) dx = \sum_{k=0}^n A_k p(x_k )\omega_{n+1}(x_k)$$

因$\omega_{n+1}(x_k ) = 0$,所以上面的式子成立

充分性： 存在$f(x) \in H{2n+1}$，用$\omega{n+1}(x)$除f(x)，记商为p(x),余式为q(x),即$f(x) = p(x)\omega_{n+1}(x) + q(x)$,可得

$$\int_a^b f(x)\rho(x) dx = \int_a^b q(x) \rho(x) dx$$

因为求积公式是插值型的，因此有

$$\int_a^b q(x)\rho(x) dx = \sum_{k=0}^n A_k q(x_k )$$

因此

$$\int_a^b f(x) \rho(x) dx = \sum_{k=0}^n A_k q(x_k )$$