边缘

一般来说，边缘是图像像素变化大的区域，但是这并不绝对

如图所示，两个位置像素一样，但是我们会天然的把它区分黑白，这得益于我们对图像的整体理解。基础的图像滤波只考虑局部的因素，如果要得到更好的效果需要进行整体考虑。

边缘可以用来区分物体，是图像分类、图像裁剪、图像拼接等操作的基础。

梯度

梯度定义：

含义：是一个向量，表示沿着这个方向导数获得最大值，也就是变换最快

离散化表示

$\nabla I(x,y)=\begin{bmatrix}{ {\Bbb d} \over {\Bbb d}x}I(x,y) \\ { {\Bbb d} \over {\Bbb d}y}I(x,y) \end{bmatrix} = \begin{bmatrix}I(x+1,y)-I(x,y) \\ I(x,y+1)-I(x,y)\end{bmatrix}$

边缘检测

Sobel, Prewitt, Robert

Sobel算子为：

$\begin{bmatrix} 1 & 2 & 1\\ 0 & 0 & 0\\ -1 & -2 & -1 \end{bmatrix} \quad \begin{bmatrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1 \end{bmatrix}$

Prewitt算子和sobel算子格式相同，只是2变成了1

Robert算子：

$\begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix} \quad \begin{bmatrix} 0 & 1\\ -1 & 0 \end{bmatrix}$

水平检测和垂直检测结果

高斯-拉普拉斯(LOG)算子

拉普拉斯算子是二阶滤波器，它的形式为:

$\begin{bmatrix} 0 & -1 & 0\\ -1 & 4 & -1\\ 0 & -1 & 0 \end{bmatrix} \\或\\ \begin{bmatrix} -1 & -1 & -1\\ -1 & 8 & -1\\ -1 & -1 & -1 \end{bmatrix}$

二阶滤波器的边缘如图所示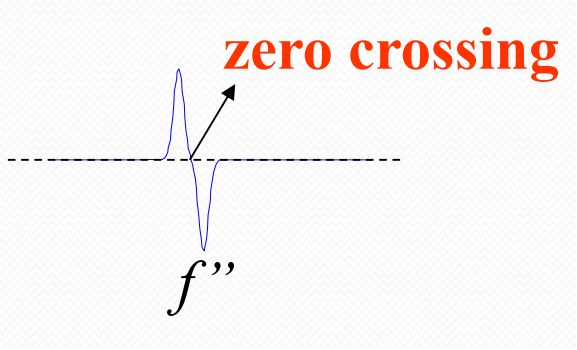

这种方式的问题是只要过零点就算边缘，无论多小的变化都会有一个响应，因此它的效果是很差的。

为了解决这个问题，可以首先使用高斯滤波器进行平滑处理，然后在使用拉普拉斯算子进行边缘检测。

实际上可以将这两个步骤进行合并

高斯算子为：

$G(x, y) = \frac{1}{2\pi \sigma^2}e^{-\frac{x^2 + y^2}{2\sigma^2}}$

其中$\sigma$是方差，方差越小图像越平缓

它的离散形式为：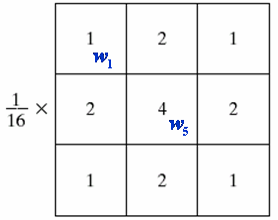

这个形式其实是$\sigma = 0.8$中心点为原点计算出来的,计算结果为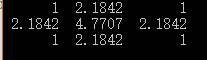具体可看

//生成高斯算子
inline double gauss(double x, double mean, double sigma)
{
	return ( exp( (-(x-mean)*(x-mean)) / (2*sigma*sigma) ) / sqrt(PI * 2.0 * sigma * sigma) );
}

void MakeGaussianVector(double sigma, myvec& GAU)
{
	int i, j;

	double threshold = 0.001;

	i = 0;
	while(1) {
		i++;
		if ( gauss((double)i, 0.0, sigma) < threshold )
			break;
	}
	GAU.init(i+1); 
	GAU.zero(); 

	GAU[0] = gauss((double)0.0, 0.0, sigma);
	for (j = 1; j < GAU.getMax(); j++) {
		GAU[j] = gauss((double)j, 0.0, sigma);
	}
}

然后将两种算子结合可以得到高斯拉普拉斯算子

$\frac{x^2 + y^2 - 2\sigma^2}{\sigma^4} e^{-(x^2 + y^2 ) / 2\sigma^2}$

我们可以选取一个$\sigma$并选择一个方形核再使用上面所说的方法进行拟合

DOG算子

DOG其实是LOG的近似，它由两个高斯函数复合而成

两个曲线一个是LOG一个是DOG

DOG算子表达式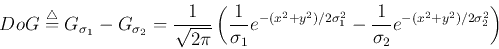

Canny边缘检测

前面的算法找到的边缘都是一些离散的点，并且边缘也不只一个像素，这种边缘对于一些处理来说不是很方便。canny算法中认为好的边缘要有如下条件：

好的检测：检测出更多的事迹边缘
好的定位：标识的边缘要和实际边缘接近
好的响应：相同边缘只被标识一次

步骤参考这篇文章

步骤：

高斯滤波
计算梯度和方向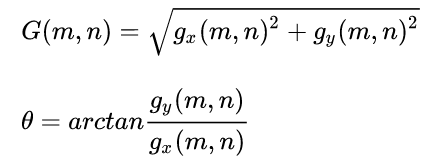：上面两个公式分别计算梯度值和梯度方向。
具体来说，假设是sobel算子，那么$g_y(m, n)$是
$\begin{bmatrix} -1 & 0 & 1\\ -2 & 0 & 2\\ -1 & 0 & 1 \end{bmatrix}$
$g_x(m, n)$是
$\begin{bmatrix} 1 & 2 & 1\\ 0 & 0 & 0\\ -1 & -2 & -1 \end{bmatrix}$
非极大值抑制：非极大值抑制目的是为了得到好的响应（相同边缘只被标识一次），因此一些同样是边缘但是强度没那么大的将被抑制到0.具体做法为
- 将梯度强度和梯度方向上的前后两个像素进行比较
  - 如果当前梯度强度比另外两个点大，则保留为边缘点，否则抑制
  通常为了精确计算，还需经过插值，如：
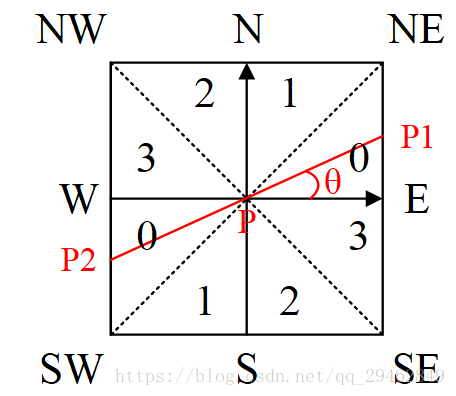
  我们采用P1, P2两个点进行计算，P1 P2两个点的获得过程为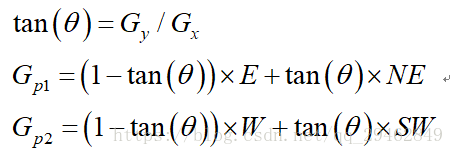
  
  注意：图中是斜率小于0的情况，因为原点在左上角
双阈值检测：经过上面的步骤之后还是会有一些噪声或颜色导致的边缘。为了消除这些边缘，认为设定高低梯度阈值, 记为$th t_l$。假设t为该点的梯度强度，如果$t > t_h$标记为强边缘像素，如果$t < t_h && t > t_l$标记为弱边缘像素，如果$t < t_l$则抑制。$t_h 和 t_l$的一种取值为$t_h = 0.12 * t{max} \quad tl = 0.1 * t{max}$
抑制孤立低阈值点：弱边缘像素是否是真正的边缘还有些争论，我们认为强边缘点一定是变元，而边缘是连续的。根据这个思想，我们可以检测所有弱边缘点，如果弱边缘点附近8个点中没有一个强边缘点则将其抑制。

FDOG算法

这张图像从整体上来看是一个松鼠，但是从右边局部来看却几乎看不出松鼠的边缘，前面说的算法最终结果中也不会有松鼠。这是因为只考虑局部的信息。

FDOG(Flow-base DOG)算法会沿着边界方向进行检查，如果发现边界的边缘还是边界则认为这是一个边界。

具体过程为：

获得ETF：计算每个像素点的梯度，获得梯度的方向（梯度计算在上面已经说明）。然后获得梯度的垂直方向，也就是(-y, x)。
ETF平滑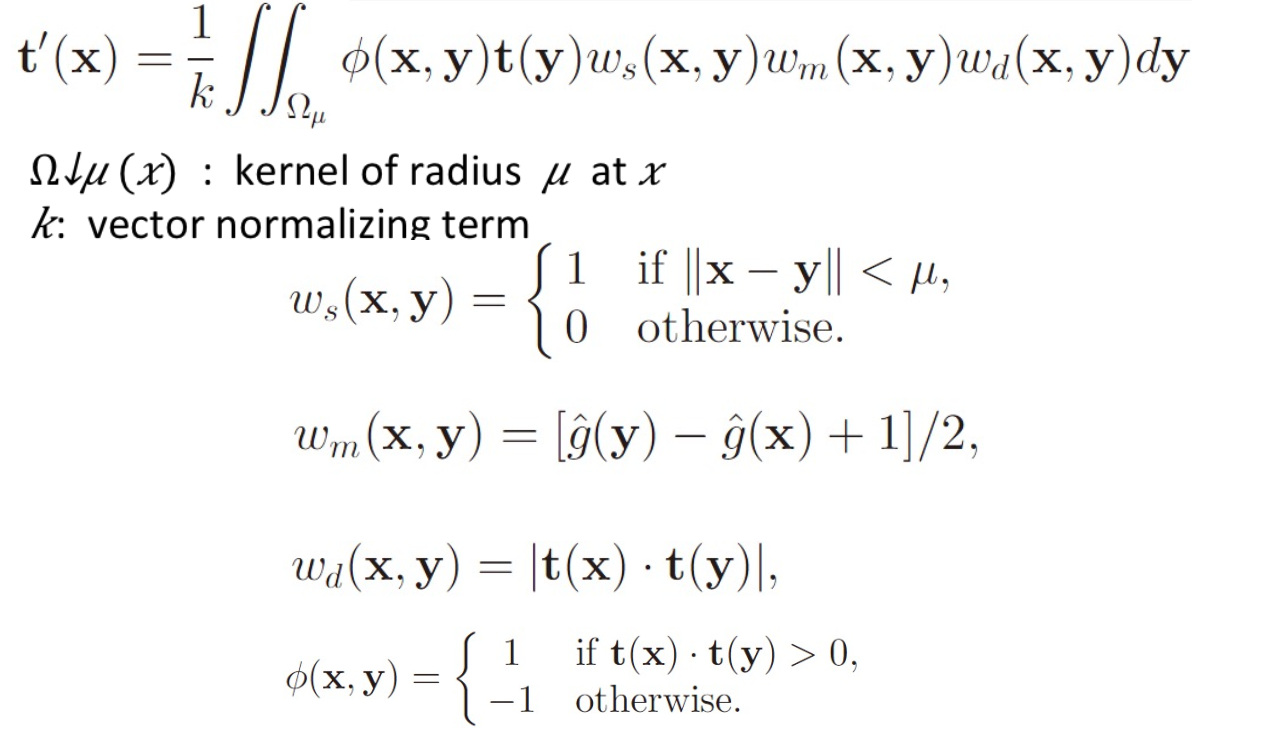：其中g是梯度的强度，t是梯度的方向

这个公式的含义是将周围的梯度进行处理后附加到当前梯度上。为了节省计算量，一般只取竖直和水平两个方向进行计算，代码为该文件的Smooth函数
生成边缘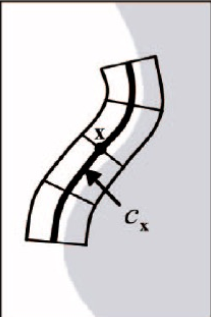：如图所示，我们需要寻找图中连续的边缘，可以首先使用DOG算法找出可能的边缘位置，然后再使用前面ETF计算的边缘方向查找边缘方向上的点是否是边缘，如果是则标记当前点为边缘。最终再进行阈值筛选
迭代：如果觉得一次运行效果不好，可以把生成的边缘加到原图中增强边缘再重复运行算法