空间域图像增强
本文最后更新于 2024年10月1日 上午
基本灰度变换
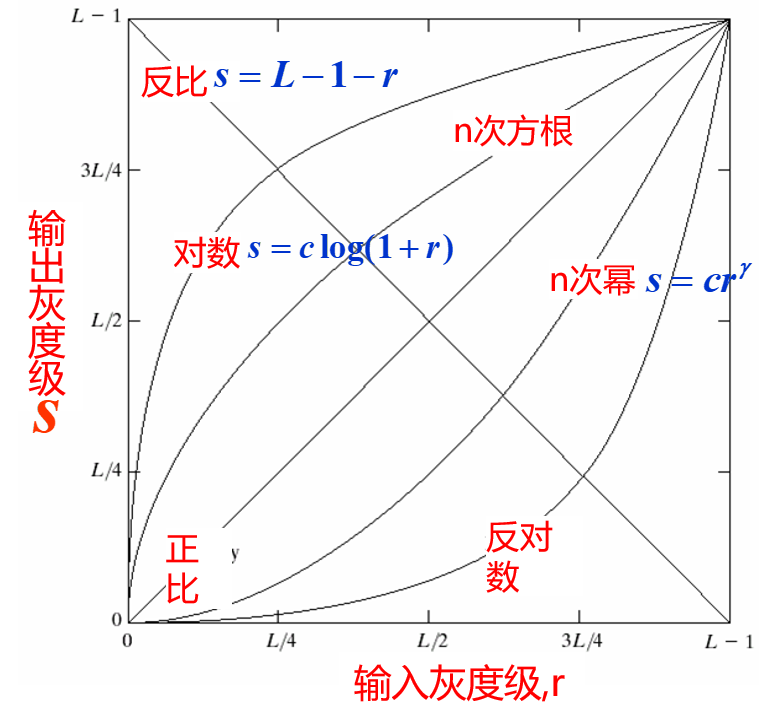
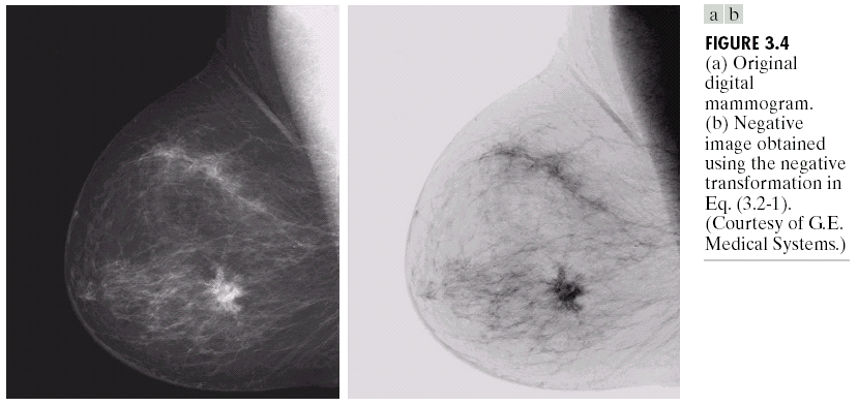
- 反转变换: 也就是图中的反比。作用是将黑图变白,白图变黑,这样可以显示出原来一些比较隐蔽的信息
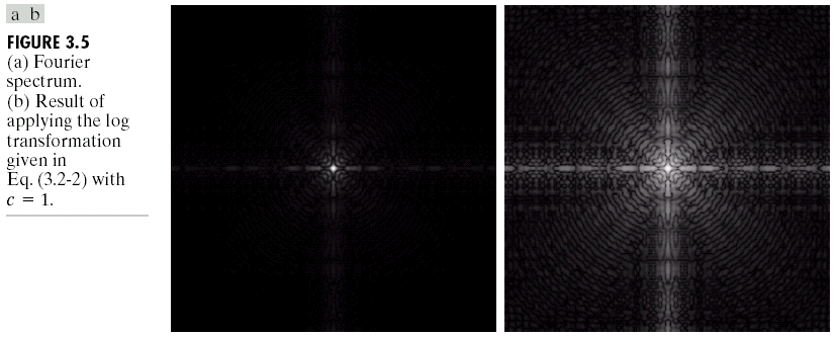
- 对数变换: 对数变换可以将一些较暗的图像变亮,并且对图像整体没有太大影响
- 幂次变换; 幂次变换可以自由选择将亮的图片变暗或者将暗的图片变亮。并且他可以达到和对数变换类似的效果。一个典型的应用是$\gamma$矫正
$\gamma$矫正是对于摄像机来说的,摄像机拍摄后的图像和真实情况往往会有一个转换。假设入射光强度为r,输出电压为v,则有:$v = C r^{\gamma}$
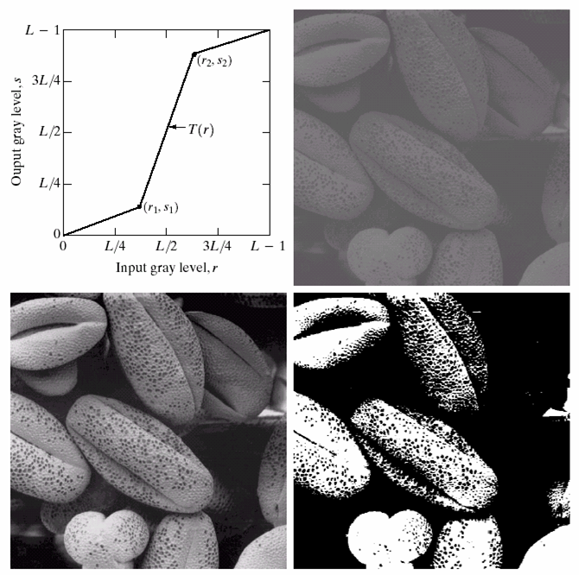
因此预先乘一个$\frac{1}{\gamma}$就可以避免光电效应,而$\gamma$值由摄像机的参数决定 - 分段线性变换: 输入和输出之间是一个分段函数,例如:
直方图处理
直方图就是统计每一种像素出现的数目,然后根据直方图进行一些处理。根据经验我们可以得出直方图分布比较均衡的图像更清楚(有对比度),例如: 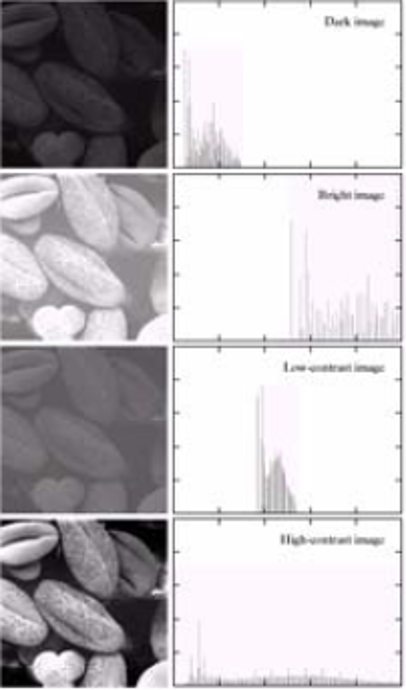
其中第四个图像就显得更清楚。
计算归一化直方图的公式为: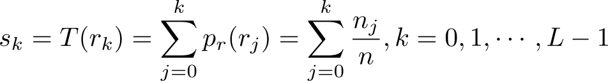
其中$n_j$是第j个灰度出现的次数,n是像素的总数。
直方图均衡化
直方图均衡化也就是让直方图像素分布尽可能平均。
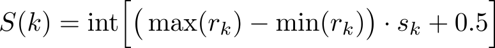
max(rk) - min(rk)也就是像素的范围,一般是255.$s_k$是归一化后的概率,0.5是为了向上取整。
然后建立了一个 k -> S(k)的映射
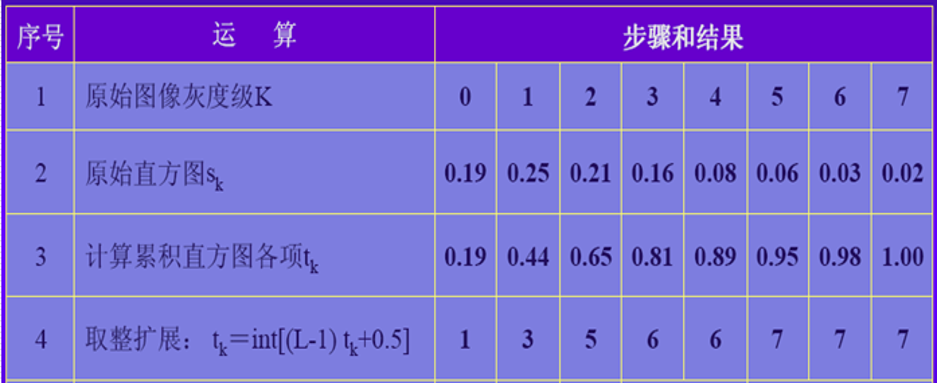
如图所示,原来的5,6,7映射到了现在的7像素
直方图规定化
直方图均衡化的缺点是不能用于交互式图像增强,均衡化只能产生一种结果。
有时候我们想依据具体情况会根据一些变换函数产生一些特定的直方图,然后根据这些直方图对原图像进行变换。
假设$p_r (r)$是原图的直方图,而$p_z (z)$是规定化的直方图。也就是$p_r -> y , p_z -> y$,现在对$p_z$求反函数变成了$p_r -> y , y -> z$,因此$p_r -> z$。这样我们就建立了从原函数到规定化函数的方法。
例:
原函数直方图结果
规定直方图的反函数结果,第5步是原来直方图生成的结果,然后将左边和右边呼唤位置得到变换后的结果。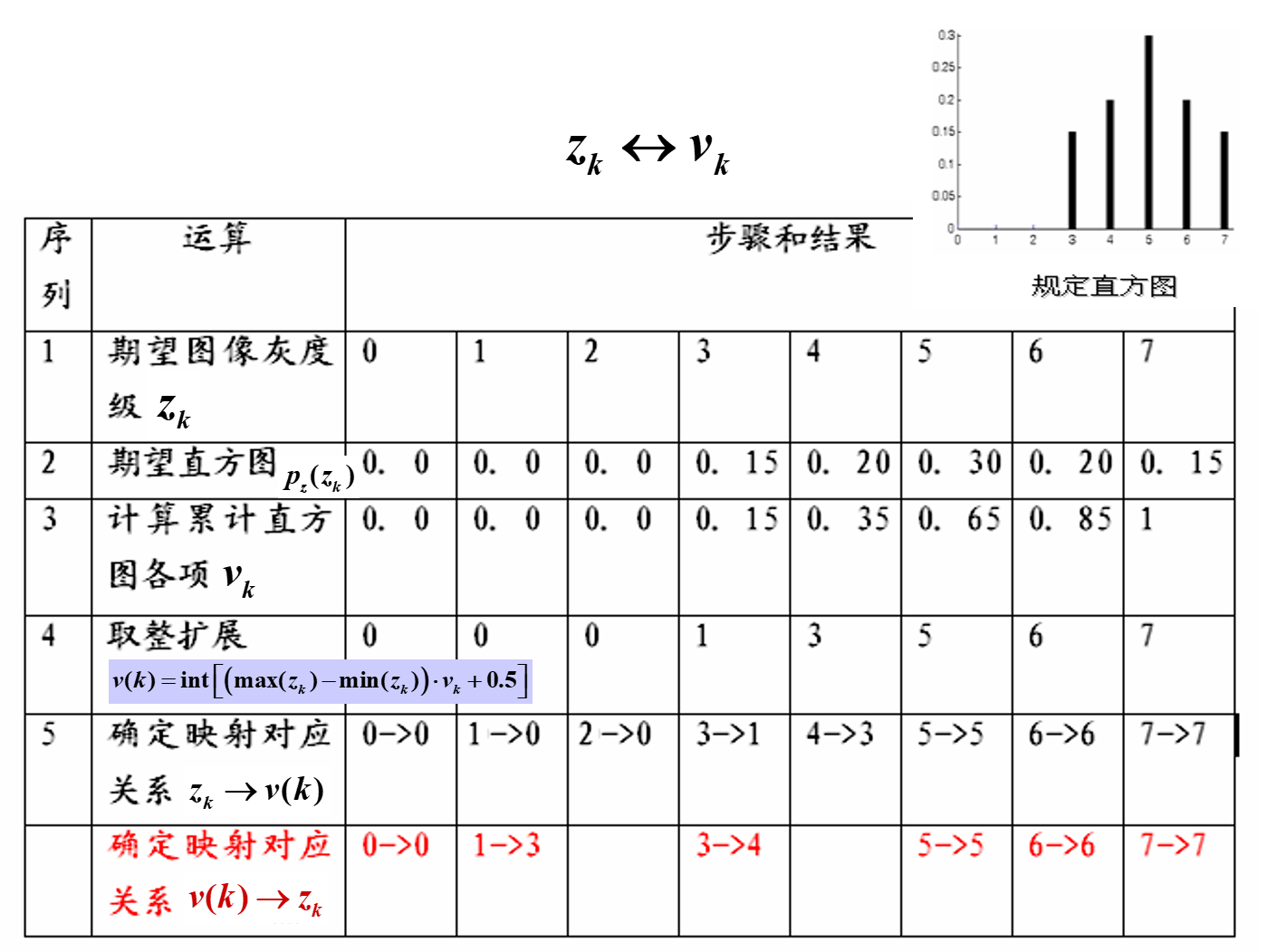
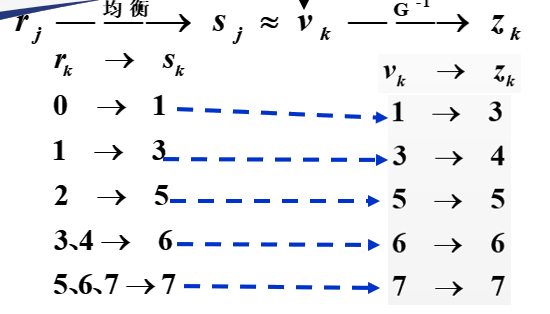
空间滤波
空间滤波也就是卷积操作,即用一个子图进行掩膜运算。公式为:
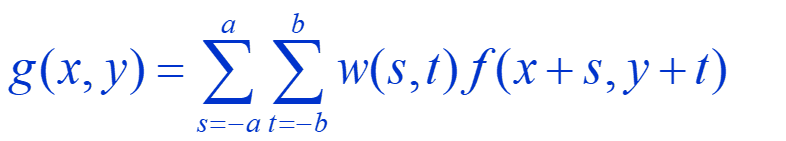
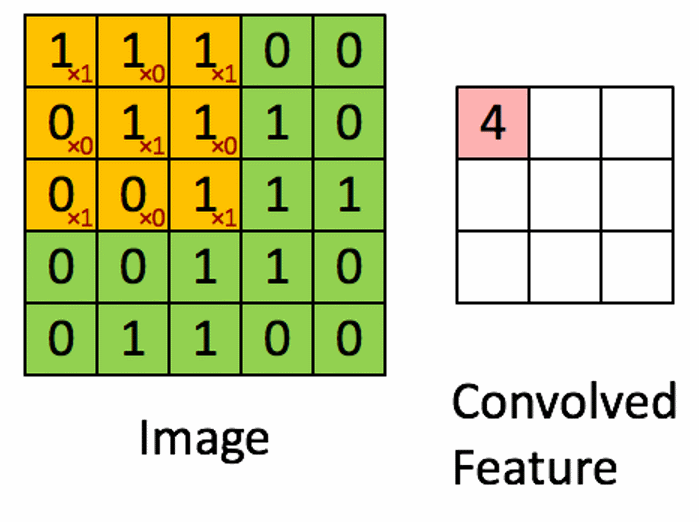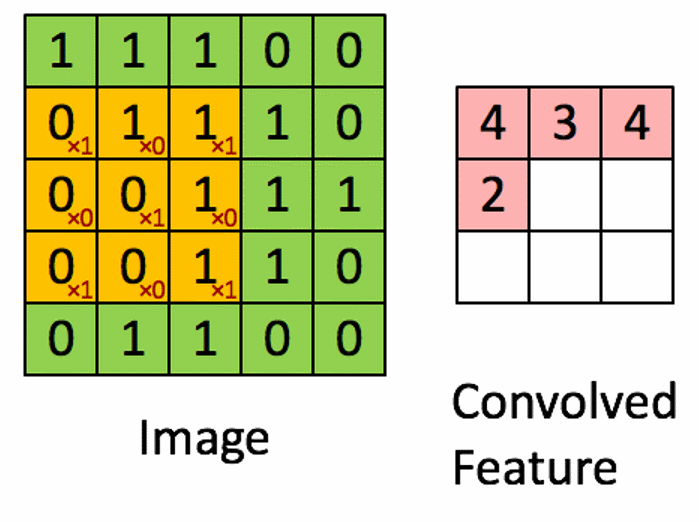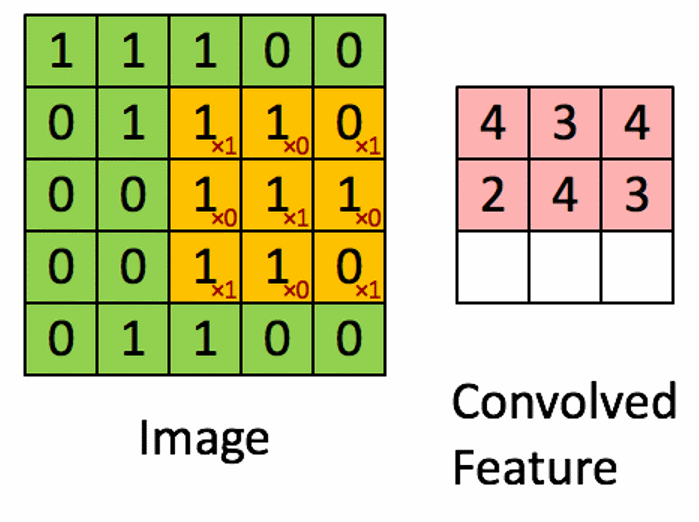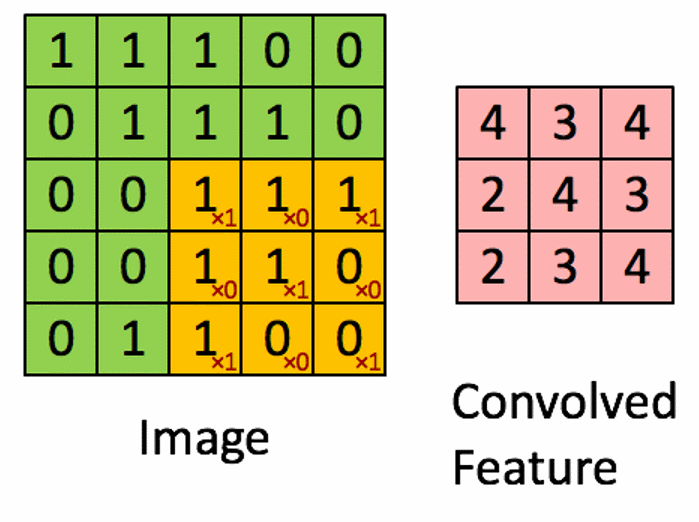
空间平滑滤波器
空间平滑滤波器是为了消除噪声。一般噪声都是和其他像素点差距比较大的点,平滑处理可以减少尖锐变化。但是他也会带来一定的负面效应也就是图片模糊化。因为图片的边缘像素也会急剧变化。
平滑线性滤波器
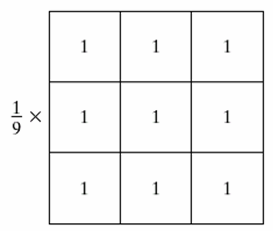
它的卷积核如上图。也就是求周围九个点的平均值。此外我们还可以使用加权平均
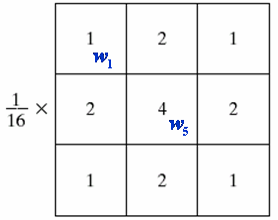
统计排序滤波器
一般是将卷积范围内的中值赋给该像素点。中值滤波可以很好的消除一些噪声点并且可以保留原有的细节,但是如果图中点、线过多可能会连带将点线删除。

中间是平滑线性滤波,右边是中值滤波效果
空间锐化滤波器
锐化是突出某些细节,一般是边缘部分。锐化处理可以借助微分的思想完成。
离散形式的一阶微分为: 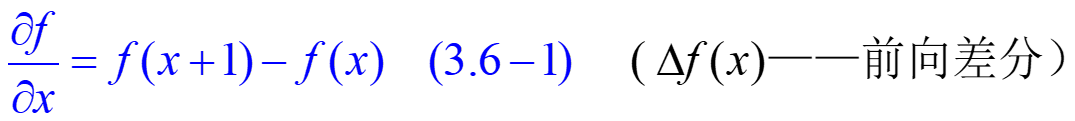
二阶微分: $\frac{\partial^2 y}{\partial^2 x} = f(x+1) + f(x-1) - 2f(x)$
拉普拉斯算子: 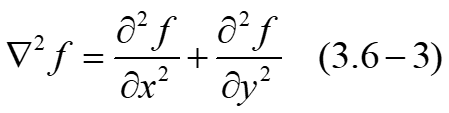
因此根据离散形式二阶微分的定义我们可以得到
对应的卷积核为:
左边就是公式中所给出的形式,右边是根据经验增强的形式
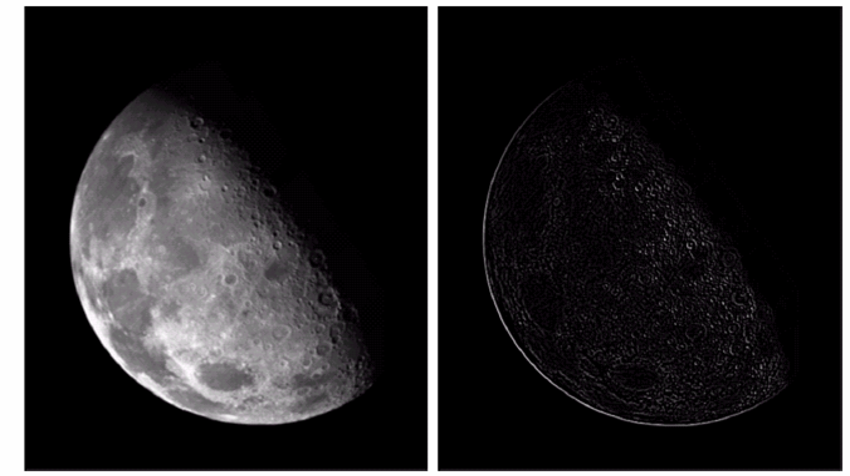
它突出了像素急剧变化的地方。
为了将突出的结果应用到原图像中,我们可以在中心位置+1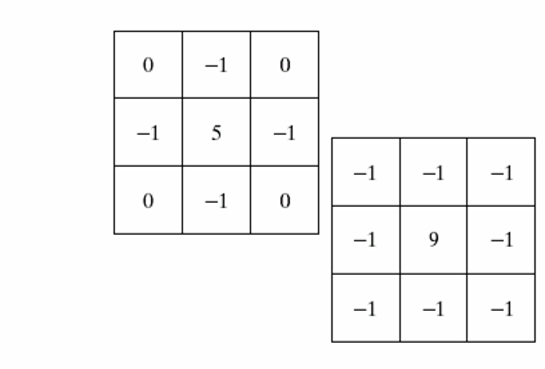
边缘检测
理想的边缘是从一个像素级突变到另一个像素级,但是实际上也是一个渐变的过程。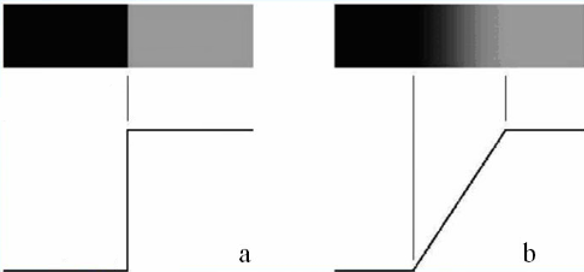 。
。
这时候我们可以使用一阶导数判断一个点是否为边缘点(导数从0到某个值),并且可以使用二阶导数还可以判断方向(只有进入边缘和处边缘才会有二阶导数)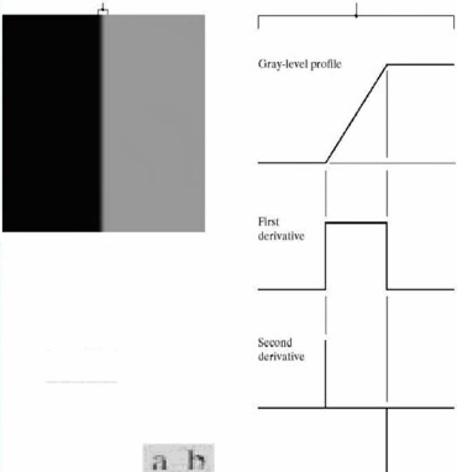
噪声对边缘检测的影响
实际情况中变化也不会那么平滑,总是会有一些上下起伏,尤其是对于摄像设备来说。
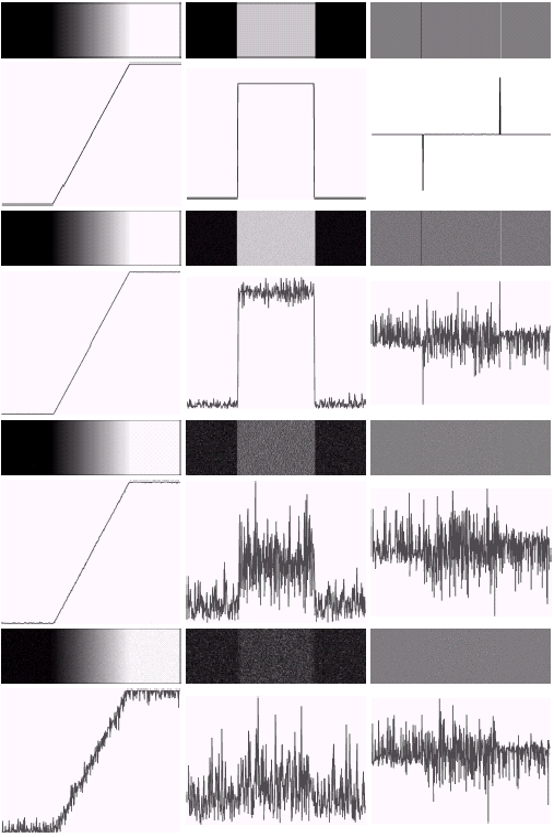
如图所示,中间是一阶导数,右边是二阶导数,在添加了1的高斯噪声情况下就变得几乎没有规律了,尤其是二阶导数。
因此二阶导数的抗干扰性是比较差的,如果我们使用拉普拉斯算子(二阶导数)做边缘检测的话,最好先对图像进行平滑处理。
此外还有一些一阶导数算子可以用于平滑处理
Sobel算子
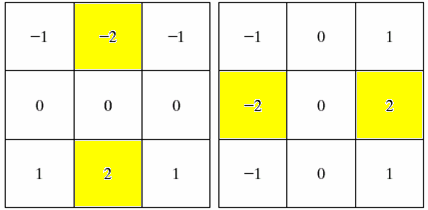
这种算子对水平和垂直的边缘具有非常好的检测效果