引入

空间角度的图像增强是非常直观且符合我们认知的，但是图像如何引入频率呢？

在图像中频率可以看成是图像变换速率。频率越大图像强度（亮度/灰度）变换越快，因此有日常所说的高频信息和低频信息。

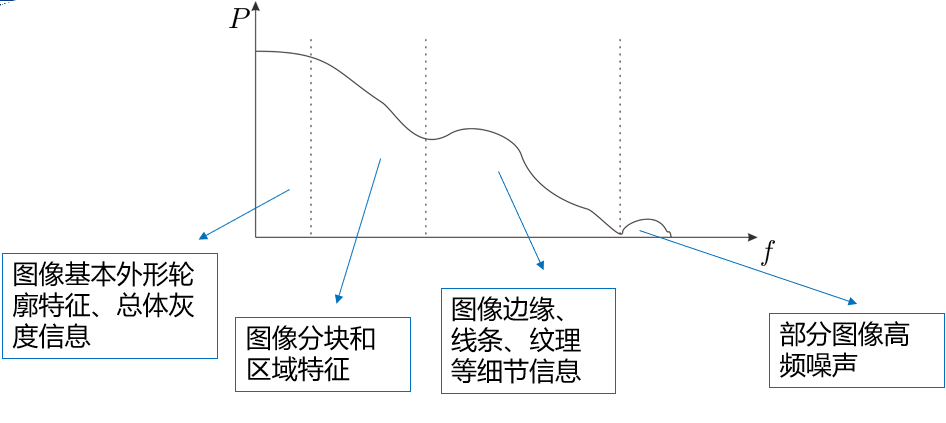
傅里叶变换

傅里叶变换可以将空间上的信息转化为频率上的信息，也就是他可以捕获变化的剧烈程度。

连续变换及反变换公式：

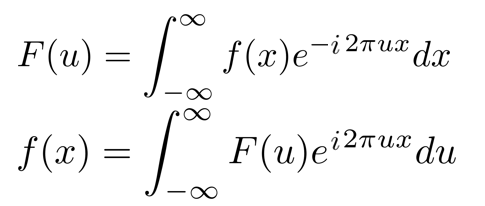
可以得出离散形式的变换和反变换公式：

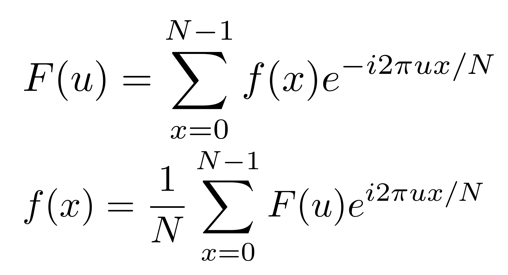
根据欧拉公式$e^{ix} = cos(x) + i \, sin(x)$可得：

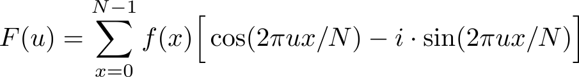
求解出每个u的函数后可以把它划分成实部和虚部，然后进行一些处理

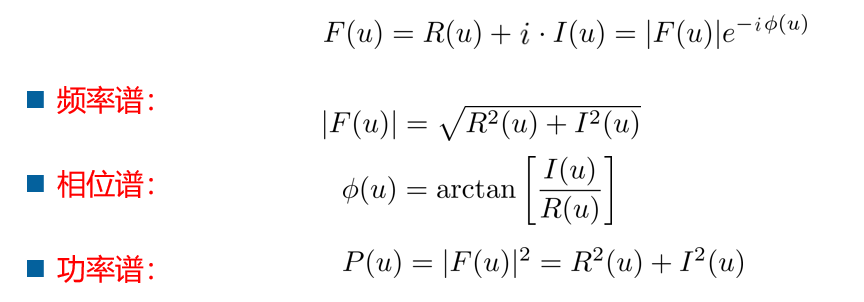
例：假设采样点为$x_0 = 0.5 , x_1 = 0.75 , x_2 = 1.00 , x_3 = 1$

$\begin{aligned} F(0) &= \frac{1}{4} \sum_{x_0}^{3} f(x) e^0\\ &= \frac{1}{4} [f(0) + f(1) + f(2) + f(3)] = 3.25\\ F(1) &= \frac{1}{4} \sum_{x_0}^{3} f(x) e^{\frac{-i 2 \pi x}{4}}\\ &= \frac{1}{4}(-2 + i) \end{aligned}$

根据上面的求解我们可以看出F(0)也就是低频信息其实就是求所有像素的平均值，而高频信息则是所有像素进行了一些转换，

二维离散傅里叶变换（DFT）

一个M$\times$N大小的图像傅里叶变换为：

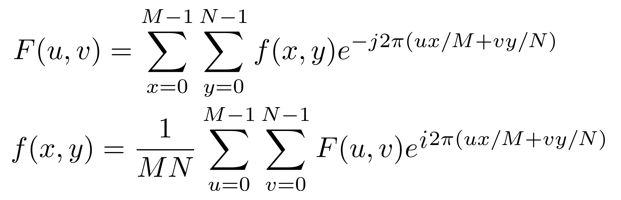
平移性

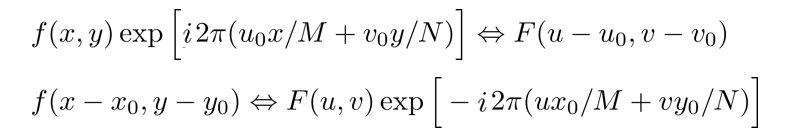
第一个公式表示原函数乘一个指数函数相当于新的函数平移
第二个公式表示原函数平移相当于在傅里叶函数上乘一个指数函数。并且他还表示原函数平移不改变傅里叶函数的频率

证明：

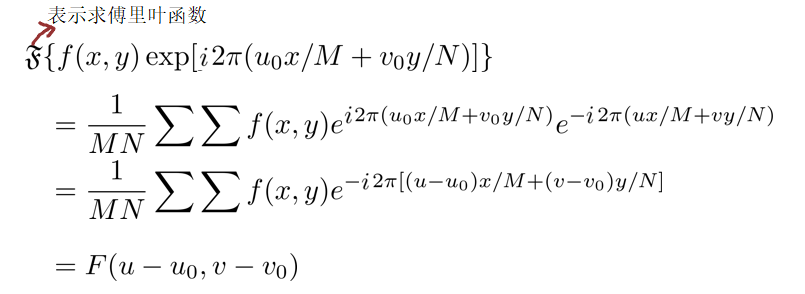
根据这个性质我们可以得出f(x, y)$(-1)^{x+y}$的傅里叶变换原点被设置在u=M/2, v=N/2(需要用到$e^{i\pi}$=-1)

周期性

$F(u, v) = F(u+M, v) = F(u+M, v+N)$

这个性质可以认为图像的上下左右都是重复的图像，也就是这个图像是无限平铺的纹理

根据上面两个性质可以将低频点变到中间，方便观察

如图所示，根据平移性可以将原点变到中间，而根据周期性可以认为部分隐藏的重复图像显示出来，或者是显示区向左下角移动。

而变换后的图像可以很清楚的看出一些特征。图像中比较亮的线可以看成原图像中一些边的信息。并且整个图像中心频率最低，越往外频率越高。

频率域滤波

频率域滤波的统一步骤：

使用傅里叶变换进行转换并且乘以$(-1)^{x+y}$进行变换
使用滤波函数H(u, v) F(u, v)得到滤波后的函数G(u, v) = H(u, v) F(u, v)
使用反傅里叶变换转换回原来的函数并且乘以$(-1)^{x+y}$

基本滤波器

陷波滤波器

陷波滤波器希望像素平均值为0。根据前面傅里叶函数求解可知F(0, 0)就是像素平均值，因此只需要将H(0, 0)置0即可

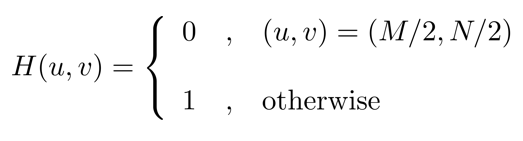
平滑滤波器

平滑滤波器也就是低通滤波器，将频率高的部分给筛除掉。依照这种思想，我们很容易想出理想低通滤波器。

理想低通滤波器的滤波函数为：

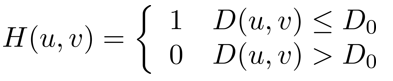
它的含义为只有中间的一点频率有值，高于这段频率全部置为0.

振铃现象

振铃现象指的是在经过处理之后会在灰度值变化处产生剧烈震荡，导致边缘模糊。而产生它的主要原因在于如果某个频率域函数为矩形，那么将它进行反变换得到的图形为右图

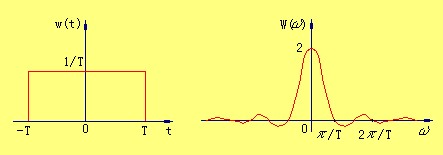
巴特沃斯滤波器

n阶巴特沃斯滤波器的形式为:

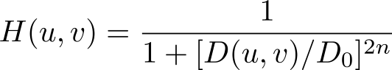
它的三维图像类似于: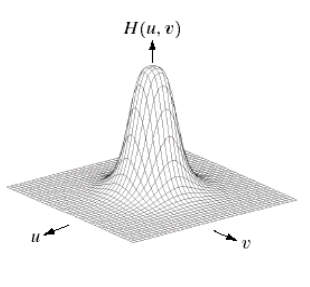

一阶巴特沃斯没有振铃，但是到2阶就开始有振铃，并且阶数越高振铃效应越明显。

高斯低通滤波器

函数形式为：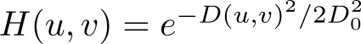
高斯滤波器没有振铃现象

锐化滤波器

高通滤波器可以 1 - 低通滤波器得到。因此很容易得到巴特沃斯高通滤波器和高斯高通滤波器的表达式