插值

基础

插值问题是给出一些离散的点，通过这些离散的点可以模拟出原曲线。

形式化定义：

设y = f(x) 在区间[a, b]上有定义，且已知在点$a \le x_0 < x_1 … < xn \le b$上的值$y_1 , … , y_n$，若存在一个函数P(x)使得

$$P(x_i ) = y_i \quad i = 0, 1, 2 ... n$$

P(x)则为f(x)的插值函数，[a, b]为插值区间。

多项式插值

构建多项式P(x) = $a_0 + a_1 x + … + a_n x^n$来模拟f(x)。假设有[a, b]上有n+1个已知点。根据定义有：

$$\left\{\begin{matrix} a_0 & + & a_1 x_0 & + & ... & + & a_n x_0^n & = & y_0\\ a_0 & + & a_1 x_1 & + & ... & + & a_n x_1^n & = & y_1\\ \vdots & & \vdots & & & & \vdots & & \\ a_0 & + & a_1 x_n & + & ... & + & a_n x_n^n & = & y_n \end{matrix}\right.$$

它是齐次非线性方程组且为范德蒙德矩阵，因此它的行列式的值为

$$detA = \prod_{i,j=0,i>j}^{n} (x_i - x_j ) != 0$$

因此我们可以得知行列式不为0，所以P(x)的解是存在且唯一的

这种方法非常不稳定，有一点小的扰动就可能导致结果天差地别

function vandermonde_ans = vandermonde(x, y, n, test_x, m)
    A = zeros(n+1, n+1);
    for i = 1:n+1
        for k = 0:n
            A(i, k+1) = x(i)^k;
        end
    end
    factor = A \ y;
    vandermonde_ans = zeros(1, m);
    for i = 1:m
        for k = 0:n
            vandermonde_ans(i) = vandermonde_ans(i) + factor(k+1) * test_x(i)^k;
        end
    end
end

拉格朗日插值

给定两个点，他们的两点式为：

$$L_1 (x) = y_k \frac{x_{k+1} - x}{x_{k+1} -x_k } + y_{k+1} \frac{x-x_k}{x_{k+1} - x_k}$$

我们可以把y的系数作为一个函数，即$L1 (x) = y_k l_k (x) + y{k+1} l_{k+1}(x)$.$l_k (x)$有一些特殊的性质

$$\begin{aligned} l_k (x_k) = 1 , l_k (x_{k+1}) = 0\\ l_{k+1} (x_k ) = 0, l_{k+1}(x_{k+1}) = 1 \end{aligned}$$

这符合我们插值函数的需要，即x=$x_k$时y=$y_k$。我们将它扩展就可以得到拉格朗日插值多项式了。

$$\begin{aligned} l_k (x) = \frac{(x-x_0 )\dots (x - x_{k-1})(x-x_{k+1})\dots(x-x_n )}{(x_k - x_0 ) \dots (x_k - x_{k-1})(x_k - x_{k+1}) \dots (x_k - x_n )}\\ \\ L_n(x_j ) = \sum_{k=0}{n} y_k l_k (x_j ) = y_j , j=0,1, ..., n \end{aligned}$$

其中$l_k (x)$是系数函数，它具有$x=x_k$时$l_k (x)$=1，$x=x_j \quad j!=k$时$l_k (x) = 0$的性质。

因此范德蒙德矩阵为：

$$L_n (x) = \sum{k=0}{n} y_k l_k (x)$$

我们可以引入记号

$$\begin{aligned} \omega_{n+1} (x) &= (x-x_0 ) (x-x_1 )\dots(x-x_n )\\ \omega_{n+1}{\prime} (x_k ) &= (x_k - x_0 )\dots (x_k - x_{k-1})(x_k - x_{k+1})\dots (x_k - x_n ) \end{aligned}$$

function lagrange_ans = lagrange(x, y, n, test_x, m)
    lagrange_ans = zeros(1, m);
    denominator = ones(1, n+1);
    for i = 1:n+1
        for k = 1:n+1
            if i == k
                continue;
            else
                denominator(i) = denominator(i) * (x(i) - x(k));
            end
        end
    end
    
    for i = 1:m
        numerator = 1;
        for k = 1:n+1
            numerator = numerator * (test_x(i) - x(k));
        end
        for k = 1:n+1
            lagrange_ans(i) = lagrange_ans(i) + y(k) * numerator / ((test_x(i) - x(k)) * denominator(k));
        end    
    end
end

误差估计

定理： 设$f^{(n)}(x)$ 在[a, b]上连续， $f^{(n+1)}(x)$在(a, b)内存在，且$L_n (x)$是符合条件的插值多项式，则

$$R_n (x) = f(x) - L_n (x) = \frac{f^{n+1}(\xi )}{(n+1)!} \omega_{n+1}(x)$$

其中$\xi$在(a, b)中。并且$\omega_{n+1}(x)$的最大值容易求，所以关键是$\frac{f^{n+1}(\xi )}{(n+1)!}$

证明： 根据定义，在这些插值点上值一定是0，因为我们可以把$R_n (x)$改写为

$$R_n (x) = K(x)(x-x_0 )(x-x_1 )\dots(x-x_n ) = K(x)\omega_{n+1}(x)$$

将x看成[a, b]上的固定点，做函数

$$\phi(t) = f(t) - L_n (t) - K(x)(t - x_0 )(t- x_1) \dots (t-x_n )$$

因此$\phi(t)$在$x_0 , x_1 … x_n$和x处为0.根据罗尔定理，在$\phi^{\prime}(t)$在$\phi(t)$两个零点之间至少有一个零点，由此类推.$\phi^{n+1}(t)$在(a, b)内至少有一个零点

$$\phi^{n+1}(\xi) = f^{n+1}(\xi) - (n+1)!K(x) = 0\\ K(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}$$

根据这个公式，我们可以得出$f^{n+1}(\xi)$的值是0就没有误差，因此多项式的级数只需要大于f(x)的求导次数就可以无限逼近

牛顿插值

牛顿插值多项式是根据点斜式进行的。点斜式：

$$P_1 (x) = f(x_0 ) + \frac{f(x_1 ) - f(x_0 )}{x_1 - x_0}(x-x_0 )$$

他可以看成零次插值的$P_0 (x) = f(x_0 )$的修正，即$P_1 (x) = f(x_0 ) + a_1 (x - x_0 )$

而三个点的二次插值可以表示为$P_2 (x) = f(x_0 ) + a_2 (x - x_0 )(x-x_1 )$

其中$a_2$为：

$$\begin{aligned} a_2 &= \frac{P_2 (x_2 ) - P_1 (x_2 )}{(x_2 - x_0 )(x_2 - x_1 )}\\ &= \frac{\frac{f(x_2 ) - f(x_0 )}{x_2 - x_0} - \frac{f(x_1 ) - f(x_0 )}{x_1 - x_0}}{x_2 - x_1} \end{aligned}$$

均差

根据上面我们可以得出一些规律.我们称$f[x_0 , x_k ] = \frac{f(x_k ) - f(x_0 )}{x_k - x_0}$为一阶均差，$f[x_0 , x_1 , x_k ] = \frac{f[x_0 , x_k ] - f[x_0 , x_1 ]}{x_k - x_1}$为二阶均差,推广为：

$$f[x_0 , x_1 ,\dots , x_k ] = \frac{f[x_0 , x_1 , \dots , x_{k-2} , x_k ] - f[x_0 , x_1 , \dots , x_{k-2} , x_{k-1}]}{x_k - x_{k-1}}$$

性质：

• k阶均差可表示为函数值的线性组合，即

$$f[x_0 , x_1 , \dots , x_k ] = \sum_{j=0}^{k} \frac{f(x_j )}{x_j - x_0 )\dots(x_j - x_{j-1})(x_j - x_{j+1})\dots(x_j - x_k )}$$

这个性质表明均差和节点的排列顺序无关，成为均差的对称性，即$f[x_0 , x_1 , \dots , x_k ] = f[x_1 , x_0 , x_2 , \dots , x_k ] = \dots = f[x_1 , \dots , x_k , x_0 ]$

因此可以得出：

$$f[x_0 , x_1 , \dots , x_k ] = \frac{f[x_1 , x_2 , \dots , x_k ] - f[x_0 , x_1 , \dots , x_{k-1}]}{x_k - x_0}$$

• 若f(x)在[a, b]上存在n阶导数，且节点$x_0 , x_1 , \dots , x_n \in [a, b]$,则n阶均差与导数的关系为 $$f[x_0 , x_1 , \dots , x_n ] = \frac{f^{n}(\xi)}{n!}$$

牛顿插值多项式

根据均差定义我们可以得到：

$$\begin{aligned} f(x) &= f(x_0 ) + f[x, x_0 ](x - x_0 )\\ f[x, x_0 ] &= f[x_0 ,x_1 ] +f[x_0 ,x_1, x](x-x_1 )\\ f[x, x_0 , x_1 ] &= f[x_0 , x_1 , x_2 ] + f[x, x_0 ,x_1 , x_2] (x-x_2 )\\ \vdots\\ f[x, x_0 , \dots , x_{n-1}] &= f[x_0 , \dots , x_n ] + f[x, x_0 ,\dots , x_n ] (x - x_n ) \end{aligned}$$

最终的式子为：

$$f(x) = f(x_0 ) + f[x_0 ,x_1 ] (x - x_0 )(x-x_1 ) +... + f[x_0 , x_1 ,\dots , x_n ] (x-x_0 ) \dots (x-x_{n-1}) + f[x, x_0 , \dots , x_n ]\omega_{n+1}(x)$$

最后一项是插值余项和前面说的插值余项形式相同。

均差计算可以使用均差表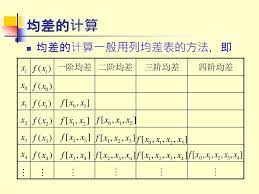

function newton_ans = newton(x, y, n, test_x, m)
    average_table = zeros(n+1);
    average_table(1, :) = y;
    newton_ans = zeros(1, m);

    for i = 2:n+1
        for k=i:n+1
            average_table(i, k) = (average_table(i-1, k) - average_table(i-1, k-1)) / (x(k) - x(k- i + 1));
        end
    end
    
    for i = 1:m
        temp = 1;
        for k=1:n+1
            newton_ans(i) = newton_ans(i) + temp * average_table(k, k);
            temp = temp * (test_x(i) - x(k));
        end
    end
end

查分形式的牛顿插值公式

实际应用中经常会用到等距节点$x_k = x_0 + kh \quad (k=0,1,\dots , n)$的情形，这里h成为步长，此时插值公式可以简化。

查分是微分的离散形式，$\Delta fk = f{k+1} - f_k$，称$\Delta f_k$为以h为步长的一阶差分。类似的有

$$\Delta^n f_k = \Delta^{n-1}f_{k+1} - \Delta^{n-1}f_k$$

为了表示方便，引入两个常用的算子：

$$If_k = f_k ,\, Ef_k = f_{k+1}$$

I称为不变算子，E称为位移算子，因此可以推出

$$\begin{aligned} \Delta f_k &= f_{k+1} - f_k = E f_k - I f_k = (E - I) f_k\\ \Delta^n f_k &= (E-I)^n f_k = \sum_{j=0}^{n} (-1)^j \binom{n}{j} E^{n-j} f_k\\ &= \sum_{j=0}^{n} (-1)^j \binom{n}{j} f_{n+k-j} \end{aligned}$$

其中$\binom{n}{j}$也就是$C_n^j$

均差和差分的关系

$$f[x_k , x_{k+1}] = \frac{f_{k+1} - f_k}{x_{k+1}- x_k} = \frac{\Delta f_k}{h}\\ f[x_k , x_{k+1} , x_{k+2}] = \frac{f[x_{k+1}, x_{k+2}] - f[x_k , x_{k+1}]}{x_{k+2} - x_k} = \frac{1}{2h^2}\Delta^2 f_k\\ f[x_k , \dots , x_{k+m}] = \frac{1}{m!\, h^m}\Delta^m f_k$$

均差和导数的关系

$$\Delta^n f_k = h^n f^{(n)} (\xi )$$

我们可以使用差分表进行计算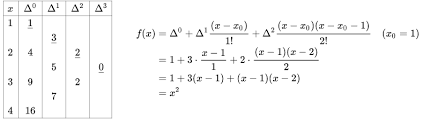

根据牛顿插值公式和均差和差分的转换关系，我们可以得到

$$\begin{aligned} P_n (x_0 + th) &= f_0 + f[x_0 , x_1 ] (x_0 + th - x_0 ) + f[x_0 , x_1 , x_2 ](x_0 + th - x_0 ) (x_0 + th - (x_0 + h) ) \dots\\ &= f_0 + t\Delta f_0 + \frac{t(t-1)}{2!}\Delta^2 f_0 + \dots + \frac{t(t-1)\dots(t-n+1)}{n!} \Delta^n f_0 \end{aligned}$$

埃尔米特插值

埃尔米特插值除了要求函数值必须和原函数相等之外，还要求在插值点上一阶导数和原函数相等。

例如两个点的埃尔米特插值模式为：

$$H_3 (x) = \alpha_k (x) y_k + \alpha_{k+1}(x)y_{k+1} + \beta_k (x) m_k + \beta_{k+1} (x) m_{k+1}$$

并且要求

$$\left.\begin{matrix} H_3 (x_k ) = y_k & H_3 (x_{k+1}) = y_{k+1}\\ H_3^{\prime} (x_k ) = m_k & H_3^{\prime} (x_{k+1}) = m_{k+1} \end{matrix}\right\}$$

并且还要求$\alpha_k (x_k ) = 1$ 为其他插值点和导数都为0，如$a_k^{\prime} (x_k ) = 0$

而$\beta$函数只有在对应点的导数值才是1，其他都是0

联立方程可以求得最终结果为:

$$R_3 (x) = (1+2 \frac{x - x_k}{x_{k+1} - x_k})(\frac{x-x_{k+1}}{x_{k} - x_{k+1}})^2 y_k + (1 + 2 \frac{x - x_{k+1}}{x_k - x_{k+1}})(\frac{x-x_k}{x_{k+1} - x_k})^2 +\\ (x-x_k )(\frac{x-x_{k+1}}{x_k - x_{k+1}})^2 m_k + (x - x_{k+1})(\frac{x-x_k}{x_{k+1} -x_{k}})^2 m_{k+1}$$

分段低次插值

根据余项的定义可知，误差的最大值和n阶导数的最大值相关。有些函数导数级次越高导数飞速增长，会导致曲线在端点附近震荡导致不准确。因此有时候采样点多了结果反而更差，这和我们的常识不符。为了解决这个问题，提出了分段插值。

分段线性插值

也就是每两个点进行一次插值，即每两个点做一条直线段，这种方法在采样点无限多的情况下可以无限逼近原曲线。

假设有n个采样点，采样点由递增，在$[xk , x{k+1}]$的区间内表达式为：

$$I_h (x) = \frac{x - x_{k+1}}{x_{k} - x_{k+1}} f_k + \frac{x - x_k}{x_{k+1} - x_{k}} f_{k+1}$$

我们可以得到它的误差限为$\frac{M_2}{8} h^2$，其中$M_2 = \underset{a \le x \le b}{max}|f^{\prime \prime}(x)|$

function linear_ans = linear(x, y, n, test_x, m)
    index = 1;
    linear_ans = zeros(1, m);
    for i = 1:m
        if test_x(i) > x(index+1)
            while test_x(i) > x(index+1) && index < n-1
                index = index+1;
            end
        end
        linear_ans(i) = (test_x(i) - x(index+1)) / (x(index) - x(index+1)) * y(index) + (test_x(i) - x(index)) / (x(index+1) - x(index)) * y(index+1);
    end
end

分段三次埃尔米特插值

和上面一样，只是插值函数变成了埃尔米特插值函数，并且此时我们需要知道导数

$$I_h (x) = (1+2 \frac{x - x_k}{x_{k+1} - x_k})(\frac{x-x_{k+1}}{x_{k} - x_{k+1}})^2 y_k + (1 + 2 \frac{x - x_{k+1}}{x_k - x_{k+1}})(\frac{x-x_k}{x_{k+1} - x_k})^2 +\\ (x-x_k )(\frac{x-x_{k+1}}{x_k - x_{k+1}})^2 m_k + (x - x_{k+1})(\frac{x-x_k}{x_{k+1} -x_{k}})^2 m_{k+1}$$

function hermite_ans = hermite(x, y, y_der, n, test_x, m)
    index = 1;
    hermite_ans = zeros(1, m);
    for i = 1:m
        if test_x(i) > x(index+1)
            while test_x(i) > x(index+1) && index < n-1
                index = index+1;
            end
        end
        a = ((test_x(i) - x(index+1)) / (x(index) - x(index+1)));
        b = (test_x(i) - x(index)) / (x(index+1) - x(index));
        hermite_ans(i) = a^2 * (1 + 2 * b) * y(index) + b^2 * (1 + 2 * a) * y(index+1) + a^2 * (test_x(i) - x(index)) * y_der(index) + b^2 * (test_x(i) - x(index+1)) * y_der(index+1);
    end
end