三维观察

三维观察是将一个三维物体投影到二维平面上的过程。一般需要经过建模变换、观察变换、投影变换、规范化变换和裁剪、视口变换

观察变换

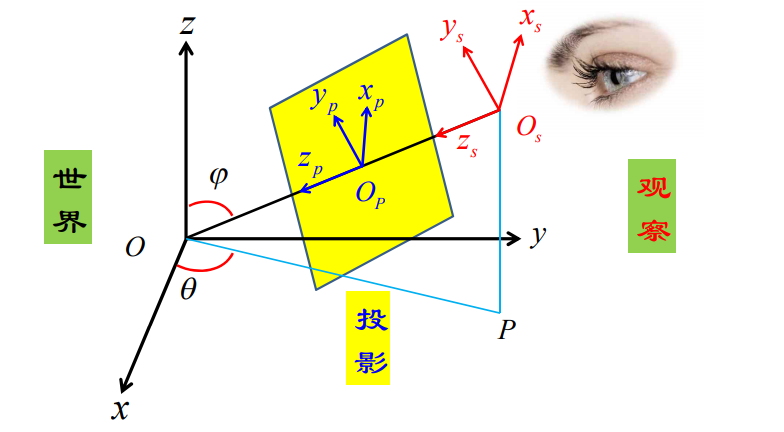
观察坐标就是人眼观察事物的坐标，我们可以使用n作为z轴正向向量，v作为眼睛上方向量也就是y，u是视线的右方也就是x。

观察变换的目的就是把物体从世界坐标系转换到观察坐标系

可以进行如下两个步骤实现转换

1. 将世界坐标的参考原点由世界坐标系原点平移到相机坐标系原点
2. 进行旋转，使nuv分别对应zyx轴

第一步可以使用矩阵：

$$M_1 = \begin{bmatrix} 1 & 0 & 0 & -x_0\\ 0 & 1 & 0 & -y_0\\ 0 & 0 & 1 & -z_0\\ 0 & 0 & 0 &1 \end{bmatrix}$$

第二步可以使用矩阵：

$$M_2 = \begin{bmatrix} x_u & y_u & z_u & 0\\ x_v & y_v & z_v & 0\\ x_n & y_n & v_n & 0\\ 0 & 0 & 0 &1 \end{bmatrix}$$

其中的分量都是nuv向量在xyz轴上的分量

综合可以得到最终的变换矩阵M = $M_2 M_1$

投影变换

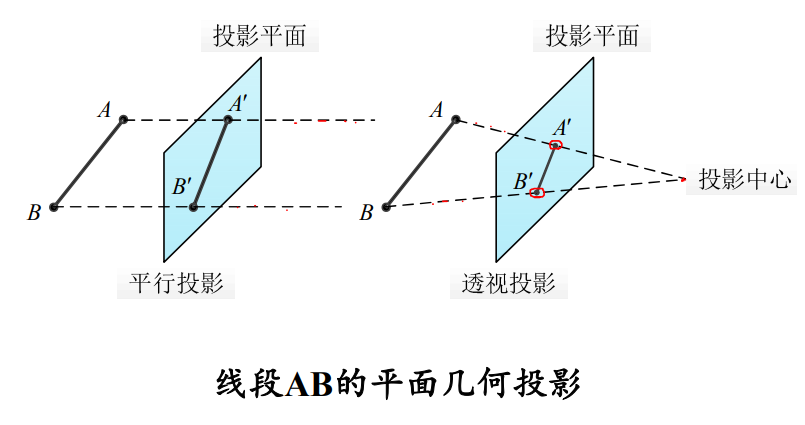
投影方式一般有两种，平行投影和正交投影。

平行投影如图所示，投影完成之后对象的有关比例不变，也就是说远的和近的在投影平面上没什么区别。它一般用于辅助绘图。

透视投影会让近的看起来大，投影的真实感比前面一种更好。

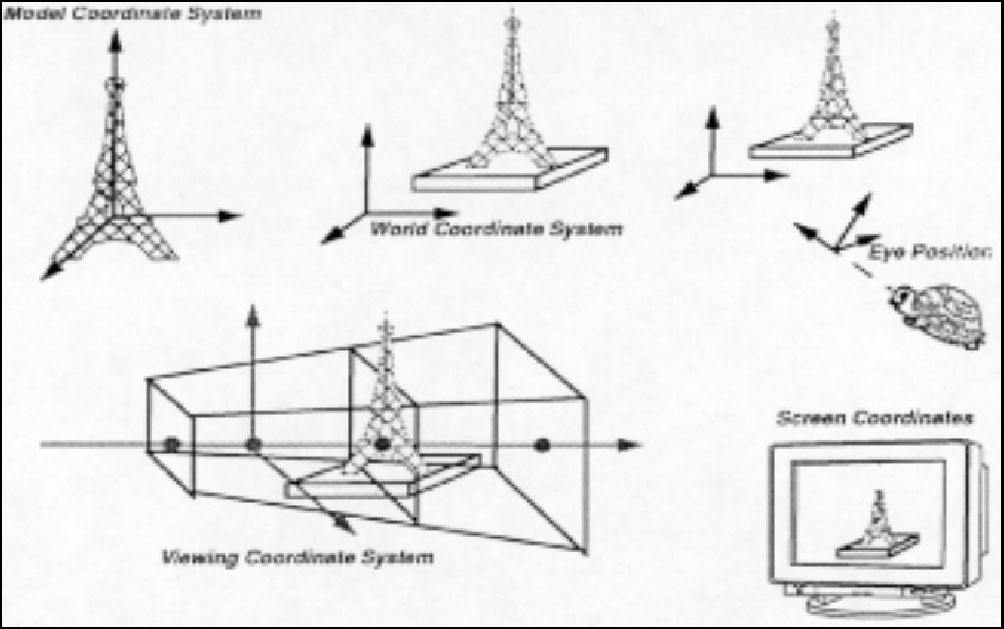
透视投影中发射光线的范围便是透视投影的角度，这个角度又可以认为是FOV(Field Of View 视线范围)。因此可以通过这个视框限制观察物体的范围，然后使用z-buffer从后往前计算每一个像素点的颜色，最终得到图像。

透视投影

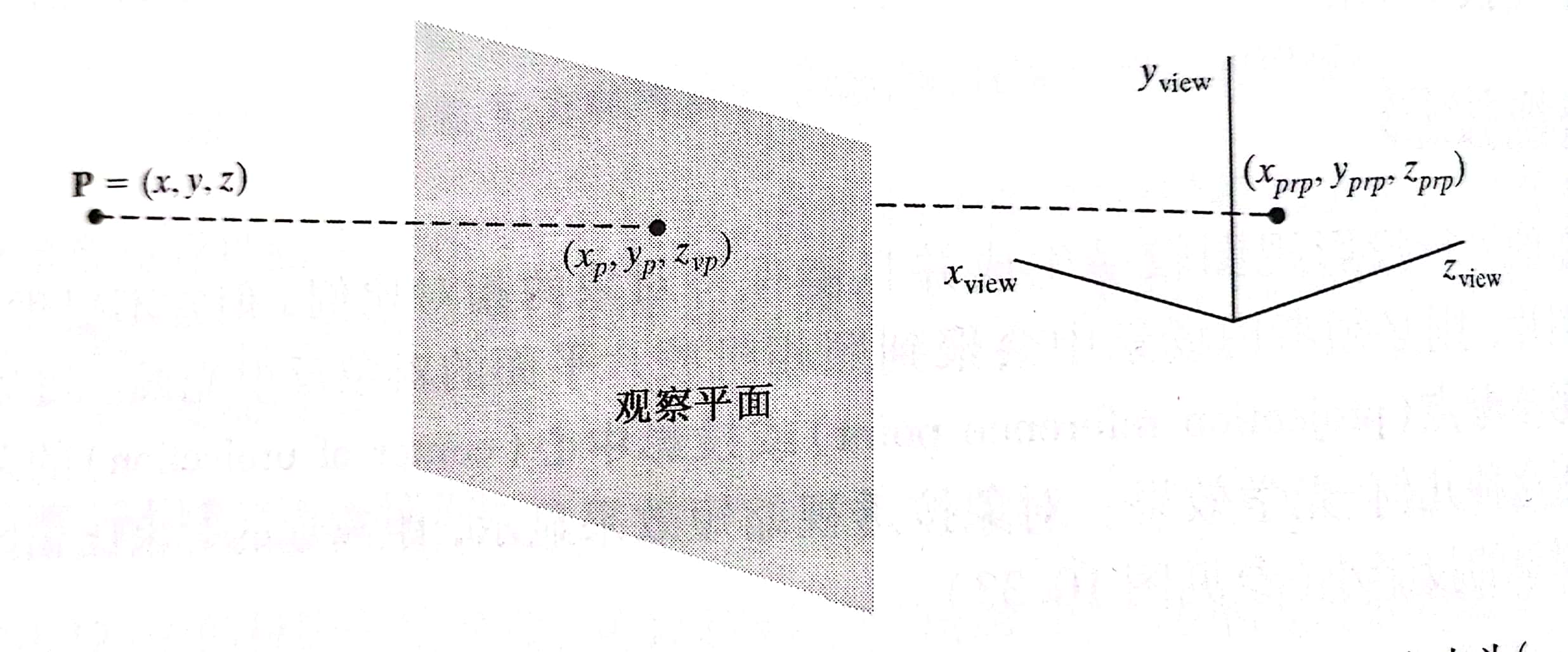
P是物体上的一个点，和观察平面的交点为($xp , y_p , z_p$)，而($x{prp}, y{prp}, z{prp}$)是投影参考点

首先观察平面点的参数方程为：

$$\begin{aligned} x^{\prime} = x - (x - x_{prp})u\\ y^{\prime} = y - (y - y_{prp})u\\ z^{\prime} = z - (z - z_{prp})u \end{aligned}$$

由于观察平面的z坐标我们是知道的，因此有$z^{\prime} = z_{vp}$，因此u为

$$u = \frac{z_{vp} - z}{z_{prp} - z}$$

然后将u带入就可以求得x和y坐标