平移

将x坐标和y坐标加上某一个值就完成了平移操作

$x^{\prime} = x + t_x \quad y^{\prime} = y + t_y$

如果使用矩阵可以表示为：

$P = \begin{bmatrix} x\\y \end{bmatrix} \quad P^{\prime} = \begin{bmatrix} x^{\prime} \\y^{\prime} \end{bmatrix} \quad T = \begin{bmatrix} t_x \\ t_y \end{bmatrix}$

并且$P^{\prime} = P + T$

三维平移和二维平移类似，只是增加了一项

旋转

二维旋转可以看

如果使用向量形式进行表示为$P^{\prime} = R P$，其中R为

$R = \begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{bmatrix}$

上面是围绕(0, 0)进行旋转的例子，如果旋转位置为($x_r , y_r$)，则变换方程为

$\begin{aligned} x^{\prime} &= x_r + (x-x_r )cos\theta - (y - y_r ) sin\theta\\ y^{\prime} &= y_r + (x - x_r ) sin\theta + (y-y_r ) cos\theta \end{aligned}$

三维旋转

如果是绕着xyz轴进行旋转，那么模式和二维旋转大致类似，但是如果按照任意旋转轴进行旋转，则需要额外进行考虑。

首先如果是平行于某一个轴，则可以先平移对象使其旋转轴于某一个坐标轴重合，然后再进行旋转。旋转完成之后平移使旋转轴回到原位置

如果该旋转轴不平行于任意旋转轴，则按照如下步骤进行：

平移对象，使旋转轴通过坐标原点
旋转对象使旋转轴于某一坐标轴重合（一般是z轴）
完成指定旋转
利用逆旋转使旋转轴回到初始方向
平移使旋转轴回到原位置

第一步需要移动到原点。假设定义旋转轴的两个端点为$P_1 (x_1 , y_1 , z_1 )$和$P_2 (x_2 , y_2 , z_2 )$。它的变换矩阵形式为

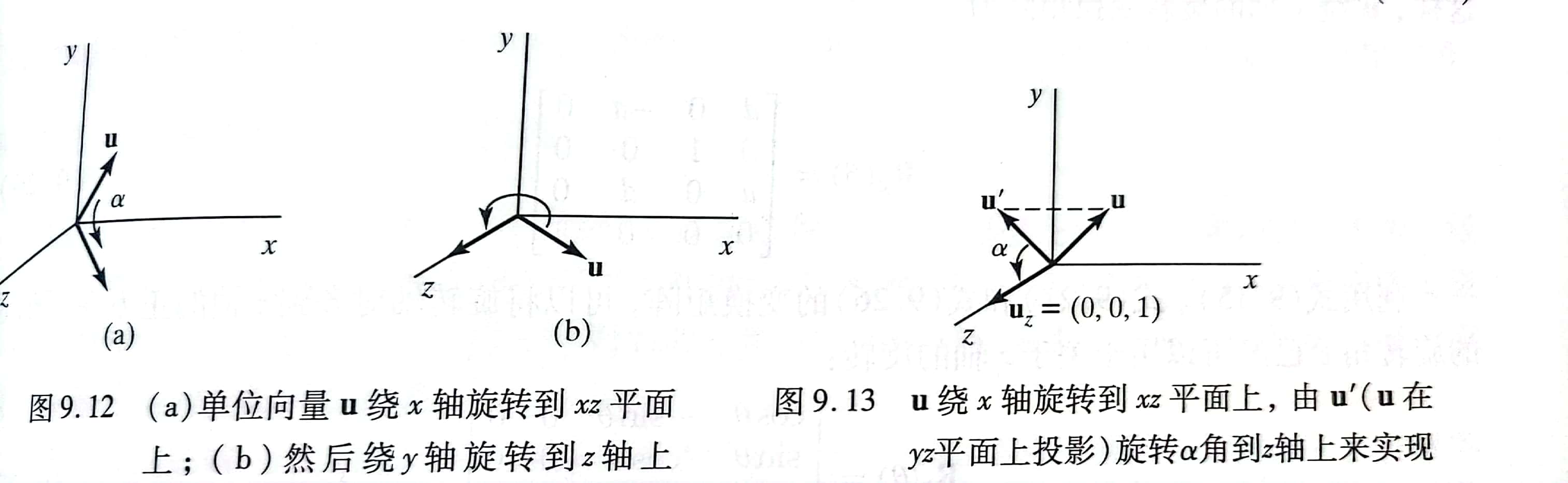
$\begin{bmatrix} 1 & 0 & 0 & -x_1\\ 0 & 1 & 0 & -y_1\\ 0 & 0 & 1 & -z_1\\ 0 & 0 & 0 & 1 \end{bmatrix}$

而第二步首先可以通过x轴旋转到xoz平面上，然后再通过y轴旋转来和z轴重合。假设旋转轴的向量为u，则旋转到xoz平面的旋转角$\alpha$为：

$cos\alpha = \frac{u^{\prime} u_2}{|u^{\prime}||u_2 |} = \frac{c}{d}\\$

$u^{\prime}$ = (0, b, c)，并且d=$\sqrt{b^2 + c^2}$

同理我们可以得到sin值为$\frac{b}{d}$，因此它的矩阵形式为

$\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & \frac{c}{d} & -\frac{b}{d} & 0\\ 0 & \frac{b}{d} & \frac{c}{d} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$

变换到xoz平面上之后，向量可以表示为(a, 0, d)，其中$cos\beta = d , sin\beta = -a$，然后使用变换矩阵

$\begin{bmatrix} cos\theta & -sin\theta & 0 & 0\\ sin\theta & cos\theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 &1 \end{bmatrix}$

三维旋转的四元数方法

四元数是一个负数带一个是不和三个虚部，写为：

$q = s +ai + bj + kc$

他也可以写为q = (s, v)，其中v是(a, b, c)

加法定义： $q_1 + q_2 = (s_1 + s_2 ) + (a_1 + a_2 ) i + (b_1 + b_2 ) j + (c_1 + c_2 ) k$
乘法： $q_1 q_2 = (s_1 s_2 - v_1 v_2 , s_1 v_2 + s_2 v_1 + v_1 \times v_2)$
平方和定义： $|q|^2 = s^2 + v \dot v$
逆： $q^{-1} = \frac{1}{|q|^2} (s, -v)$
$qq^{-1} = q^{-1}q = (1, 0)

关于四元数的理解可看

如图所示，左边是一个二维的图，怎么把它规约到一维空间中呢？一种方法是在(-1, 0)向左发出射线，那么映射到一维空间中的x是这条射线的斜率，y是和圆交点的值。

并且他还有些很好的性质，例如现在有一个点w = s + ai ，如果想要旋转$\theta$度只需要用该度数对应的函数值乘上w。

具体形式可以看上面链接中的三维及之后的部分

缩放

而二维缩放的形式为： $P^{\prime} = SP$其中S

$\begin{bmatrix} s_x & 0\\ 0 & s_y \end{bmatrix}$

三维缩放和二维缩放类似

齐次坐标

每个基本变换都可以表示为如下形式：

$P^{\prime} = M_1 P + M_2$

如果我们把所有基本变换统一起来用一个变换来表示，就产生了齐次坐标。这个坐标需要将维度进行扩展，例如(x, y)扩展到(x, y, h)，然后使用变换矩阵就可以进行变换。

平移矩阵

平移的表示形式为：$P^{\prime} = T(t_x , t_y , t_z ) P$，其中T为：

$\begin{bmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 \end{bmatrix}$

旋转矩阵

二维旋转的变换矩阵为：

$\begin{bmatrix} cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0 & 0 & 1 \end{bmatrix}$

三维旋转一般使用四元数

缩放矩阵

变换矩阵为：

$\begin{bmatrix} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$