上下文无关文法

上下文无关文法(CFG)是一个四元组(V, $\sum$, R, S)

  • V是变元
  • $\sum$是终结符
  • R: 规则，每条规则都由左边的变元和右边变元和终结符组成的字符串构成

  • S： 起始节点

    例如： S -> aSb | SS | $\varepsilon$

    二义性

    二义性指的是一个字符串可能有多种解析方式

    .

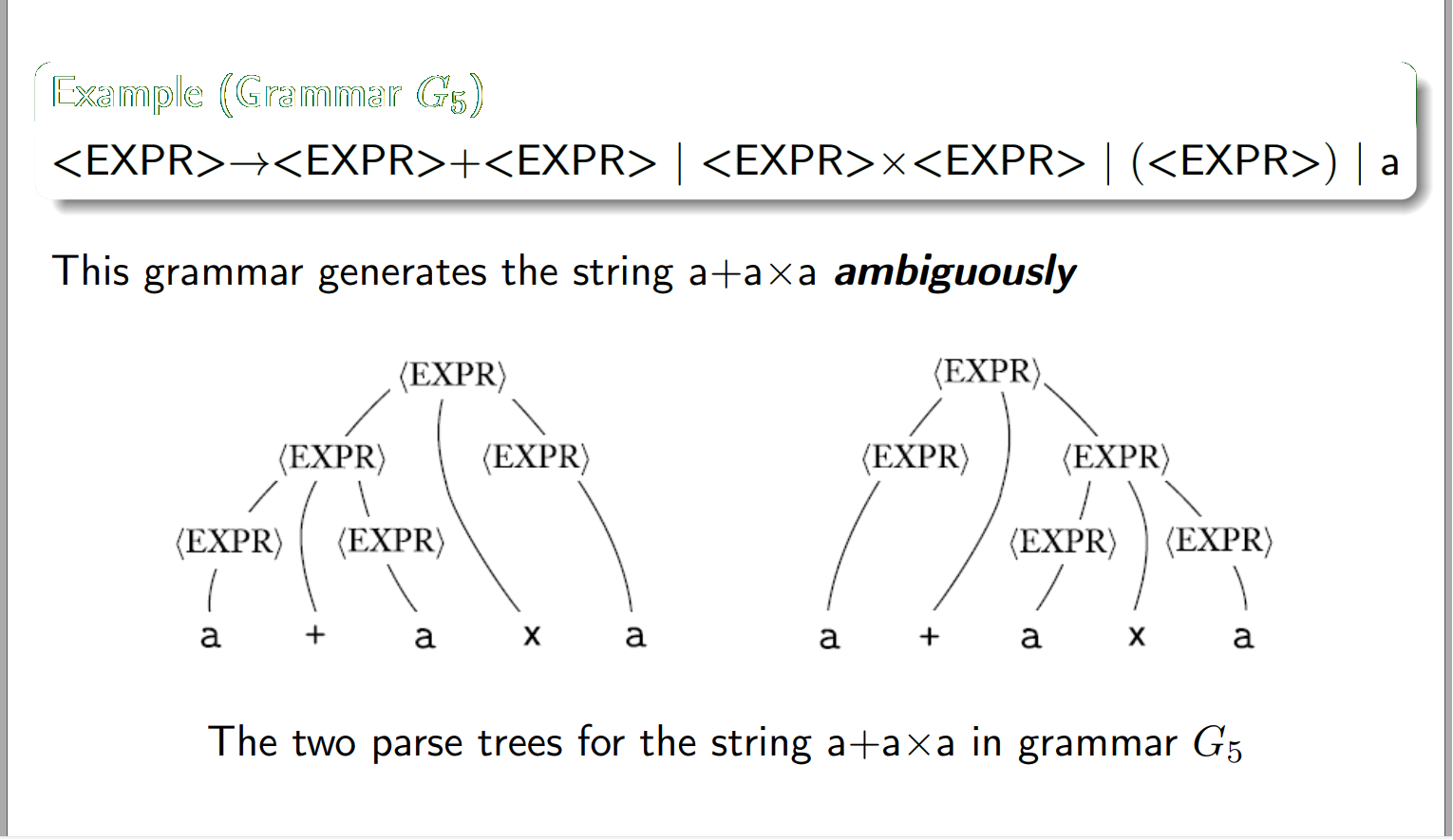    导致二义性的原因：

  • 解析顺序不同，可能最后生成的解析树是相同的。

  • 最后生成的解析树不同

    为了消除第一种导致二义性的可能，可以使用最左推导，即每次都从最左边的变元开始解析。

    二义性定义： 一个字符串可以被两个乃至更多的最左推导生成。

    乔姆斯基范式

    一个上下文无关语言的乔姆斯基范式的形式为：

  1. A -> BC
  2. B -> a
  3. S -> $\varepsilon$

证明任何上下文无关文法都可以转换成乔姆斯基范式

  • 一个上下文无关文法可以转换成乔姆斯基范式的上下文无关文法

    转换分为四个步骤：

  1. 添加一个起始变量
    添加一个$S_0$和一条规则$S_0 -> S$,其中S是原来的起始变量。这条规则是为了让起始变量不出现在右边
  2. 消除空规则如$A -> \varepsilon$
    移除A->$\varepsilon$并且A不是起始变元.
    对于每个右边出现A的位置，生成一个右边删去A的新规则，如
    R->uAv => R->uv
    R->uAvAw => R->uvAw , R->uAvw , R->uvw
  3. 删除规则A->B
    删除规则A->B
    对于每条B->u， 使用A->u代替
  4. 转换剩余规则：
    转换A->$u1 u_2 … u_k$.其中u可能是变量也可能是终结符
    将其转换成A->$u_1 A_1 , A_1 -> u_2 A_2 , … A    {k-2}->u{k-1}u_k$的形式
    如果$u_k$是终结符的话，还需要将$A_k -> u_k A    {k-1}$替换成$Ak -> U_k A{k-1}, U_k -> u_k$
    例如：A->aBc
    首先转换成A->$aA_1 , A_1-> Bc$,然后$A->U_1 A_1 , A_1 -> BC , U_1 ->a , C->c$

下推自动机

下推自动机(PDA)和NFA很像但是它多了一个栈。

形式化定义：

下推自动机是一个六元组(Q, $\sum , \tau , \delta , q_0 , F$)

  • Q: 状态
  • $\sum$: 字母表
  • $\tau$: 栈字母表
  • $\delta$: 转移函数，形式为$Q \times \sum{\varepsilon} \times \tau{\varepsilon}$ -> P(Q $\times \tau_{\varepsilon}$).它的含义为当前状态接受一个字符并且栈顶为某一个元素，跳转到另一个状态且栈顶是任意栈字母表中元素。
  • $q_0$: 起始状态
  • F: 接受状态集合

例：

  • 构建一个自动机识别语言{$0^n 1^n | n \ge 0$}

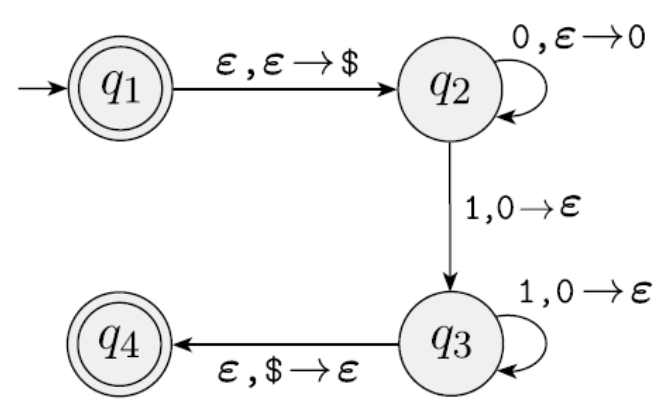
    $是栈底元素，不加上这个符号无法判断什么时候栈空。0,$\varepsilon$->0表示当前字符为0，将0放到栈顶。1,0->$\varepsilon$表示当前字符为1且栈顶字符为0，将0弹出栈。

  • 构建一个下推自动机识别语言{$a^i b^j c^k | i,j,k \ge$ 0 and i = j or i = k}

证明： 上下文无关文法和下推自动机生成的语言等价

首先证明如果某语言是上下文无关的，那么他可以被下推自动机识别

我们需要构建一个自动机。它的要求为：

  1. 将栈底符号$和文法的开始符号S拉到栈中
  2. 按照如下规则将文法转换为自动机的状态转移
    • $\delta (q{loop}, \varepsilon , A) = {(q{loop},w)$| A->w(包括变元和终结符，并且是逆序)}
      • $\delta (q{loop}, a, a) = {(q{loop}, \varepsilon$)当匹配到一个字符串中的字符时弹出
  3. 当碰到栈底字符时跳转到接受状态

例：

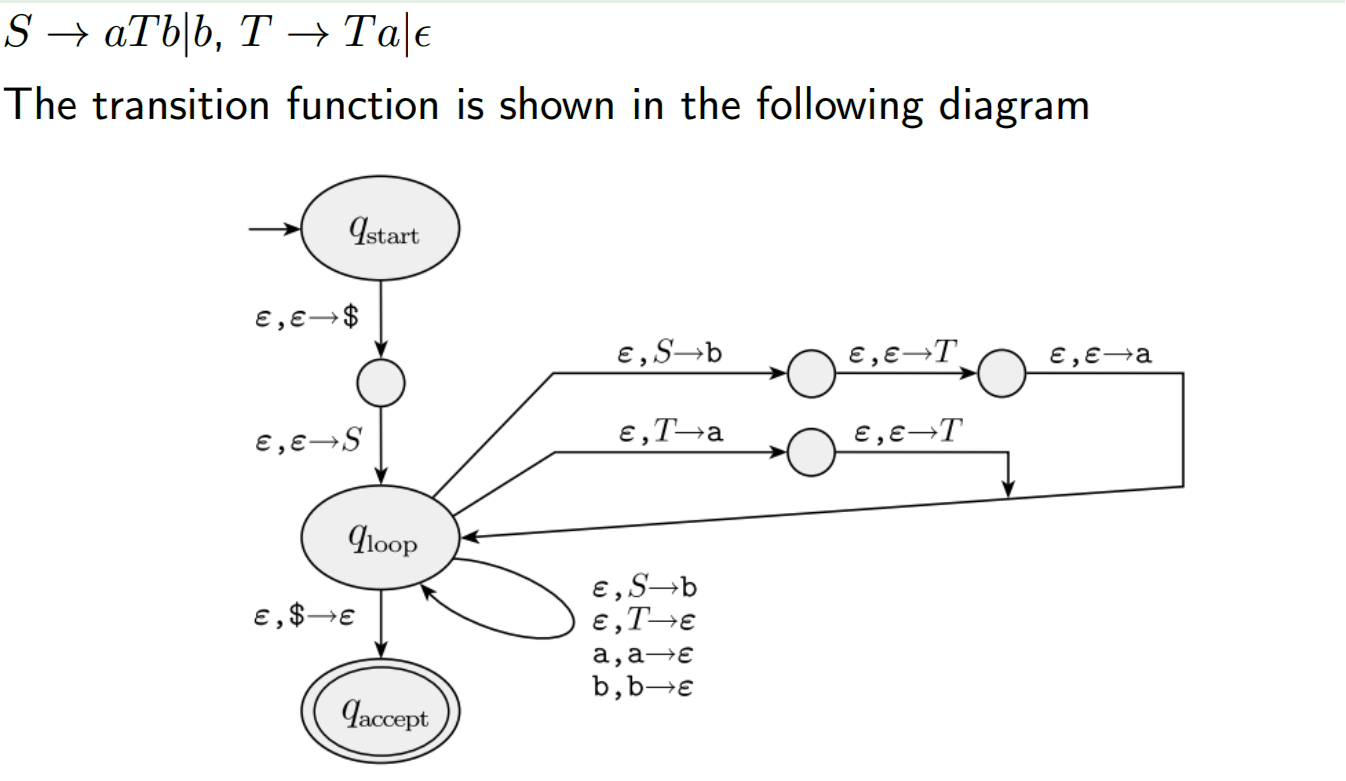
如图所示，变元到变元的规则就在loop中逆序循环，如果碰到了字符串则弹出该字符，如果是变元则运行这个变元的规则。

证明： 如果一个下推自动机可以识别某些语言，那么它是上下文无关的

为了证明这个，我们首先需要对自动机进行一些修改让他满足三个条件

  • 它只有一个接受状态
  • 它接受前是空栈
  • 每个状态转移要么拉一个进栈，要么拉一个出栈，不会同时做二者

前面两条只需要额外添加一个接受状态即可。而后面一条需要让空栈到空栈的变成压入和弹出任意字符串，如果是同时压入和弹出需要变成两个状态。

P接受x有两种可能，要么是第一个在栈中的符号在最后被弹出要么中间就被弹出，对于这两种情况分别有：

  • $A{pq} -> aA{rs}b$
  • $A{pq} -> A{pr} A_{rq}$

构建一个下推自动机{Q, $\sum , \tau , \delta , q0$,{$q{accept}$}}。G为{$a_{pq} | p , q \in Q$}.G的规则有：

  • 如果存在$\delta (p , a, \varepsilon )$包含(r, u)并且$\delta (s, b, u)$包含(q, $\varepsilon$)则将$A{pq} -> a A{rs} b$放到G中
  • 对于每个p,q,r $\in$ Q,将$A{pq} -> A{pr} A_{rq}$放到G中
  • 对于p $\in$ Q, 将$A_{pp} -> \varepsilon$放到G中

之后证明如果$A{pq}$生成x，则x可以P从p到q且为空栈。并且证明如果x可以p到q且为空栈，则$A{pq}$生成x

泵引理

定义： 对于长度大于p的任意字符串s，他都可以拆分成五部分s = uvxyz并且满足下列条件：

  • 对于所有 i >= 0 , $uv^i x y^i z \in A$
  • |vy| > 0
  • |vxy| <= p

证明：

假设b是在产生式右边变元的数量，它意味着在h步内最多有$b^h$个叶子。也就是说再走一步必定会遇到重复的符号，因此我们让泵长度p = $b^{|V| + 1}$

然后我们选取长度最小的一条路径，它必定多于h个节点，也就是说必定会有重复，记重复节点为R

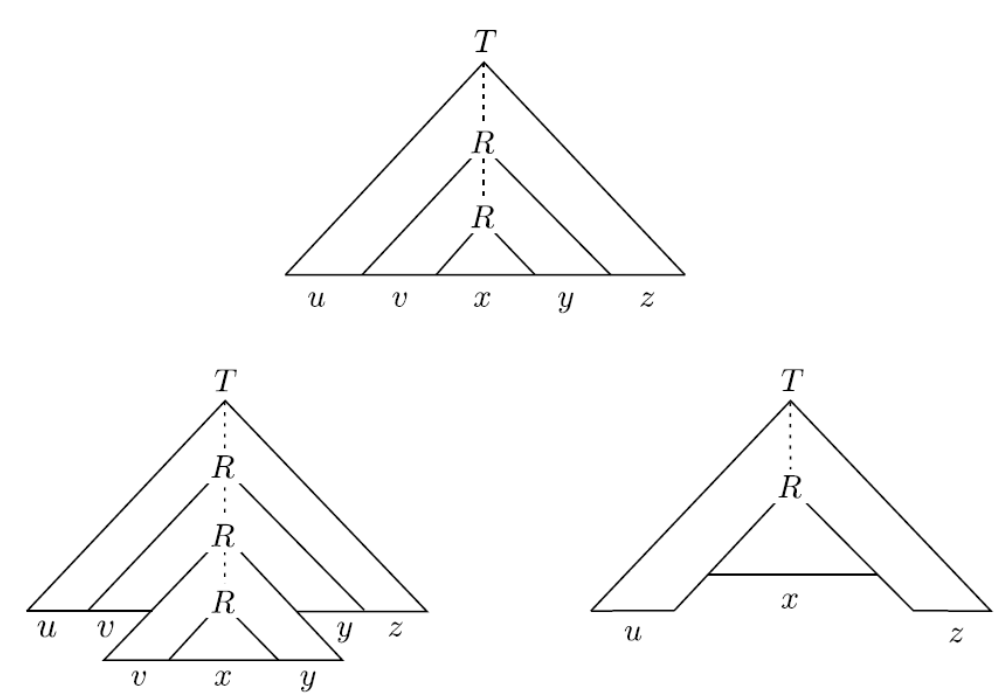
如图所示，上的R可以不断重复而重复生成v和y，因此性质1可以证明

性质2如图3，如果v和y同时为空则将上面的R删去后仍可以生成原字符串，此时长度小于|V| + 1，这就不符合我们选取最少数量节点这条

由于vxy的长度小于等于|V| + 1也就是p，因此性质三也可以证明。

例：

使用泵引理证明B = {$a^n b^n c^n | n \ge 0$}不是上下文无关的。

构造B = $a^p b^p c^p$

如果vy只有一个元素，那么只有a，b，c三种可能，重复之后都不满足条件。

如果vy有至少两个元素， 那么如果v和y中出现两种以上的元素，重复后不可能满足条件，舍弃。

如果v为a，y为b或v为b，y为c都不能满足条件。