定义

图灵机是一个七元组(Q, $\sum , \tau , \delta , q0 , q{accept} , q_{reject}$}

Q：状态集
$\sum$: 输入字母表
$\tau$: 纸带字母表 $\sqcup$是空白符
$\delta$: $Q \times \tau -> Q \times \tau \times {L, R}$
$q_{reject}$：拒绝状态

简单来说图灵机有一个纸带，并且有一个探头可以读取纸带中任意位置的数据，并且可以修改纸带中任意位置的值，纸带的初始内容就是输入的字符串，纸带上最后一个字符后的字符都是空白符。

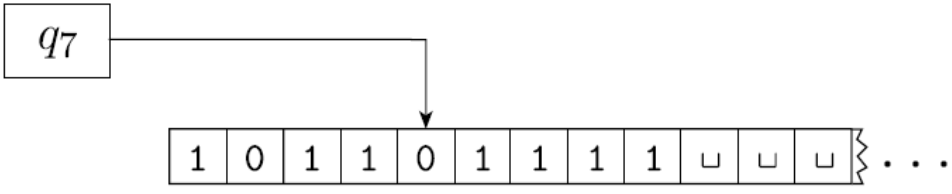
纸带的格局（当前状态的内容）：

纸带的格局由三部分内容组成，他可以使用uqv表示，其中q是读写头，uv是纸带内容

当前状态： q
当前纸带内容： uv
读写头当前位置： v的第一个字符

从当前格局跳转到下一个格局的形式化定义为：

a, b $\in \tau$, u, v $\in tau^*$, $q_i , q_j \in Q$

ua$q_i$bv 产生 u$q_j$acv 如果存在$\delta(q_i , b) = (q_j , c , L)$。其中L表示向左移动
ua$q_i$bv 产生 uac$q_j$v 如果存在$\delta(q_i , b) = (q_j , c , R$

此外对于左端点，$q_i$bv向左移动得$q_j$cv , 向右移动得c$q_j$v。对于右端点，ua$q_i$ 等价于ua$q_i \sqcup$

到了接受状态或拒绝状态就会立刻停机，不像有限自动机还可以跳转到其他状态

图灵机接受输入w也就是说存在一个格局$C_1 C_2 C_3 … C_n$使得

$C_1$是起始格局
每个$Ci 产生 C{i+1}$
$C_n$是接受格局

一些定义：

递归可枚举语言：图灵机可以识别的语言
判定器：对于一个输入会有接受、拒绝、循环三种状态，但是循环和长时间运行很难判定，大家都喜欢输入就停机的图灵机，他们被称为判定器
算法：对于任何输入都停机的图灵机，被称为总停机的图灵机，也被称为算法
递归语言：如果某一个语言可以被图灵机判定，称为图灵可判定的，也被称为递归语言

下面是正则语言，上下文无关语言，递归语言，递归可枚举语言之间的关系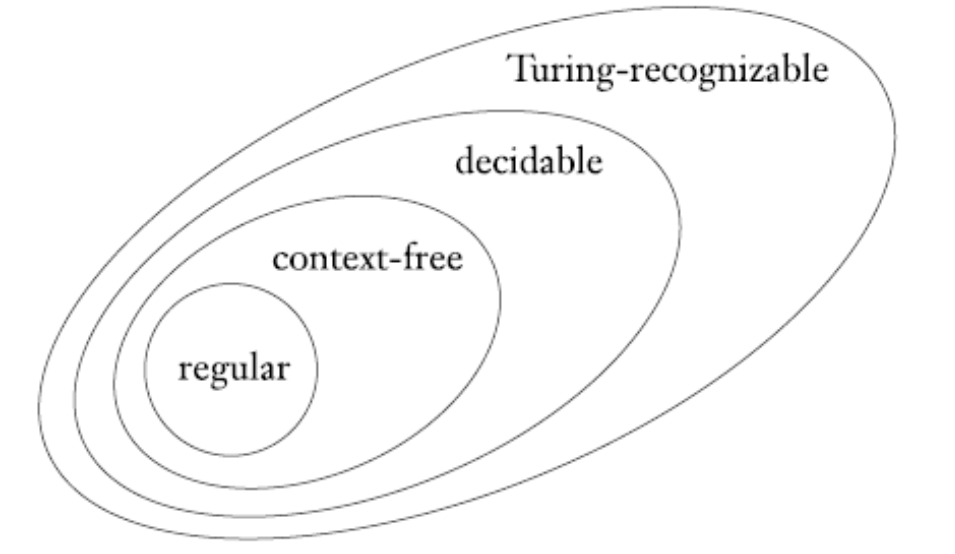

例：

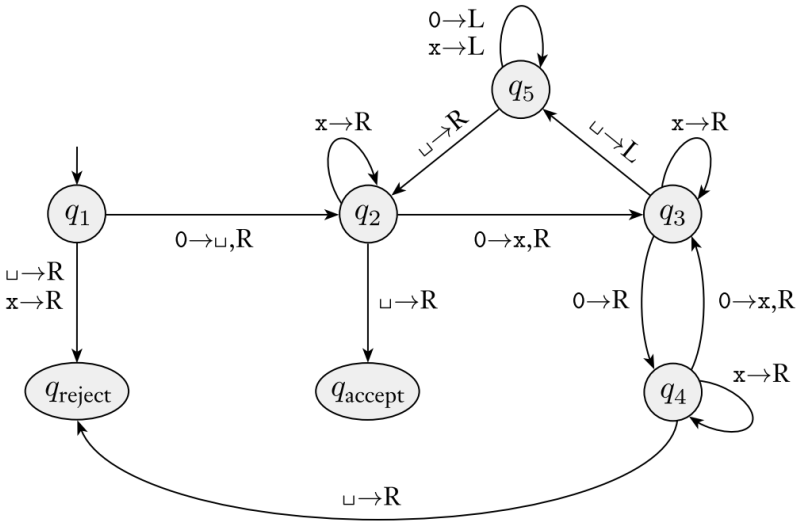
判定语言A = {$0^{2^{n}}$ | n >= 0}

思路：

隔一个字符消去一个0
如果只剩下一个0则接受
否则如果是剩下0的个数为奇数则拒绝，否则移动到最左端开始第一步

图灵机的变形

多带图灵机
多带图灵机顾名思义，他可以多条纸带同时工作，一开始只有第一条纸带有值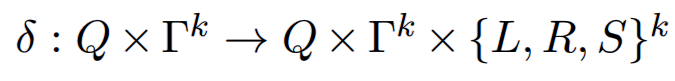

证明：多带图灵机和图灵机等价

我们可以使用一带图灵机模拟多带图灵机，假设用一个特殊字符#作为一带的开头，扫描每一个#来确定当前转态的符号，然后根据前面所指示的方式进行转移
任何时候只要移动到了某个#上面，就说明已经读到了这条纸带的尽头，然后将该区域及后面所有区域的纸带往右移一格来保证纸带的长度
非确定性图灵机
证明：非确定性图灵机和图灵机等价
- 开始时，第一条纸带包含w，第二条和第三条都是空白.把第一条纸带复制到第二条上，第三条初始化为$\varepsilon$
- 用第二条纸带去模拟N在输入w上在非确定性计算中的某个分支，在每一步动作之前，先查看第三条纸带的值
- 如果第三条纸带没有符号剩下，则该分支无效，转到第四步，否则如果是拒绝格局也转到第四步，否则如果是接受格局则接受输入
- 用字符串顺序的下一个串来替换原有的串
枚举器：
枚举器是一个k带图灵机，最后一个带是输出带

证明等价性
如果有枚举器E枚举语言A，则有图灵机M识别A， M对于输入w
- 运行E，每当E输出一个字符串时，和w进行比较，如果w曾在E的输出中出现过，则接受
  现在证明另一个方向
  
  $s_1 s_2 … s_n$是$\sum^*$中所有可能的串，如果图灵机识别语言A，则A的枚举器构造如下：
- 对于$s_1 , s_2 , … s_n$中的每一个i，M运行i步
- 如果所有计算都接受，则输出相应的$s_j$