基础算法

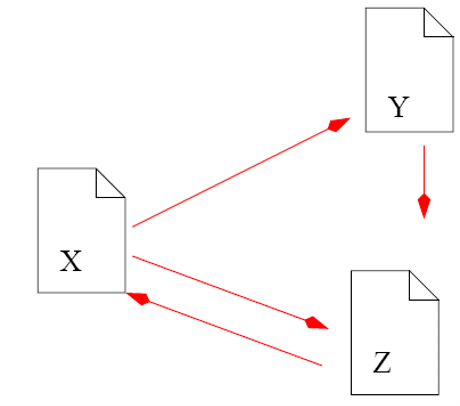
pagerank算法假设不返回已经浏览过的页面。假设给定一个页面按照页面跳转到该页面下其他页面的概率为q，浏览厌烦后随机跳转到其他页面的概率为1-q

其中$N_v$是v网页外链个数。1-q的含义是点击这个页面的概率，后面一部分是从其他页面跳转到这个页面的概率。

这种计算方式的问题是速度太慢，只有三个页面就要83次迭代。

矩阵求解

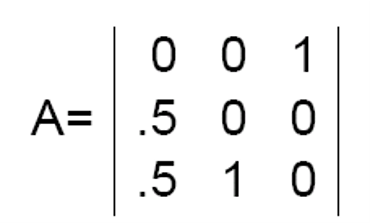
其中$A_{ij}$是第j个页面指向第i个页面的平均概率

假设$\vec{r}$是矩阵的特征向量，则从其他页面跳转到该页面按照$\vec{r} = qA\vec{r}$计算。

其中$\vec{r}$也就是前面式子中的R(v),A矩阵是前面式子中的$\frac{1}{N_v}$

而要获得初始概率可以使用$\vec{r} = \frac{1-q}{N}I\vec{r}$

其中I是单位矩阵，实际上也就是1-q

合并两个部分可以得到最终公式$\vec{r} = (qA + \frac{1-q}{N}I)\vec{r}$