时序逻辑设计
时序逻辑电路的输出是由上一刻的输出和这一刻的输入共同决定，也就是说时序电路带有记忆。
锁存器和触发器
双稳态电路
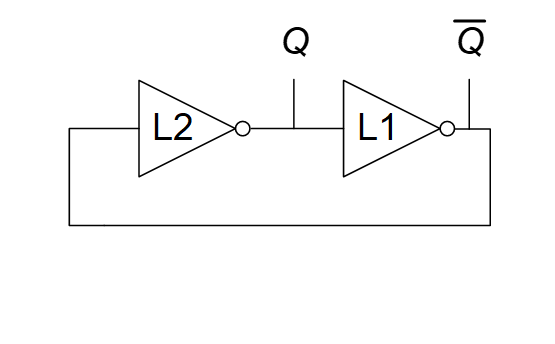
例如Q是1，则经过L1后变为0，因此$\bar{Q}$ 为0，然后又给L2输入，再回到Q还是1。所以Q始终为1，$\bar{Q}$始终为0，因此称为双稳态电路。
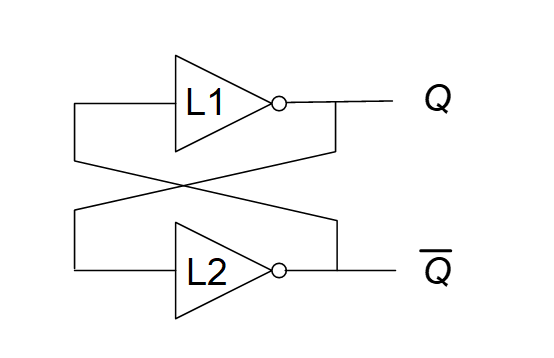
这是它的等价形式，注意这张图是有问题的，L1和L2要变换位置。
SR锁存器
上面的双稳态电路不方便输入，因此SR锁存器在双稳态电路上做了改进。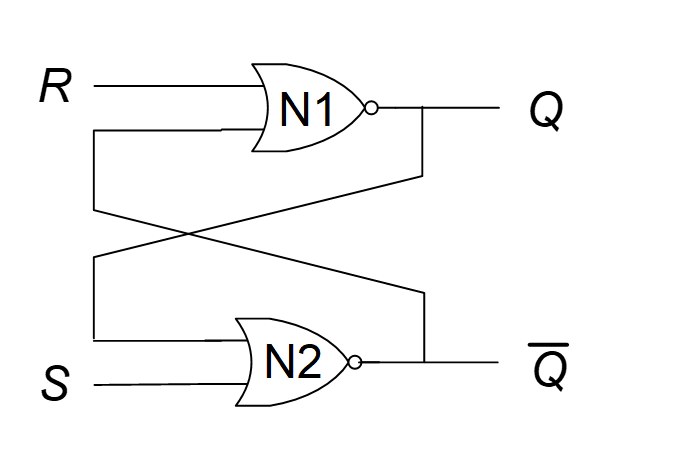
如图，添加了R和S两个输入端，当R和S为下列值时，Q输出为
| R(reset) | S(set) | $Q^+$(Q下一时刻状态) |
|---|---|---|
| 0 | 0 | Q(保持) |
| 0 | 1 | 1(置位) |
| 1 | 0 | 0(复位) |
| 1 | 1 | x |
主要是二者都为1的情况。二者都为1时，Q和$\bar{Q}$都是0，这就违背了Q和$\bar{Q}$的本意。
并且在二者变成0（保持状态)之后，如果是同时变成0，那么Q和$\bar{Q}$先同时变成1，然后同时变成0，这样来回震荡。
当然同时改变时不可能的，如果R先变成0，那么Q为1，$\bar{Q}$为0。反之Q为0，$\bar{Q}$为1.
因此二者同时为1时会造成电路不稳定（亚稳态），因此二者同时为一是禁止的。
D锁存器
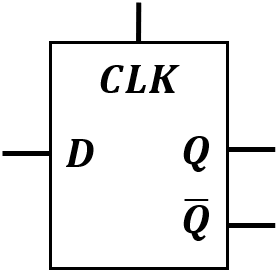
- CLK=0, $Q^+$ = Q，也就是锁存器的值不会变化，锁存器是不透明的
- CLK=1， $Q^+$ = D, 这时候可以把它当成一根导线，锁存器是透明的（没有作用）。
这是他的原理图，他在SR锁存器上做了一些补充，避免了因为S和R同时为1导致的一些奇奇怪怪的现象。
D触发器
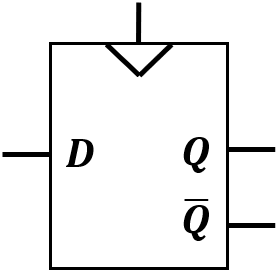
D触发器时在CLK从0到1的瞬间对D进行采样，然后一直保持这个状态，知道下一次从0到1才会重新改变。
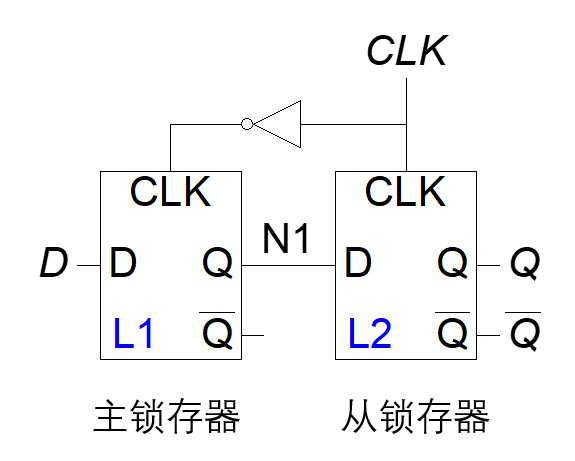
当CLK=0时，主锁存器开启，也就是说D的状态就是N1的状态，但是从锁存器关闭，总的输出还是上一时刻的输出。
CLK=1，从0到1的一瞬间把主锁存器关闭，也就是说N1的状态就是D最后时刻的状态，然后从锁存器打开，N1的状态直接输出
触发器的分类：
按逻辑功能分为：RS触发器、D触发器、JK触发器（J和K同时为1时翻转）、T触发器（保持和翻转，实际上是将JK型触发器中J和K合并为一个信号）。
按触发方式分为：电平触发器、边沿触发器和脉冲触发器。
按电路结构分为：基本RS触发器和钟控触发器。
按存储数据原理分为：静态触发器和动态触发器；
寄存器
寄存器是由一个共享的CLK控制多个D触发器组成。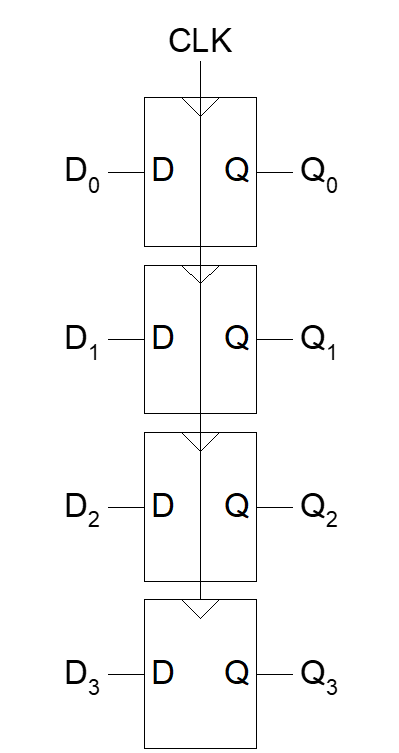
带使能端的触发器
EN=0时，使能端处于保持状态（也就是CLK=0的状态）。EN=1时，不影响正常工作。
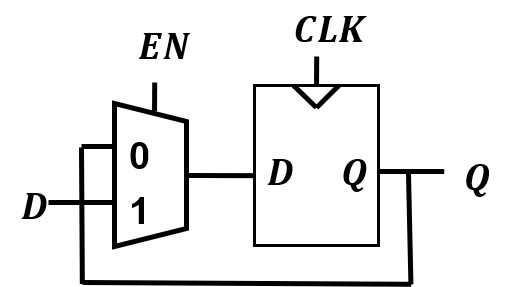
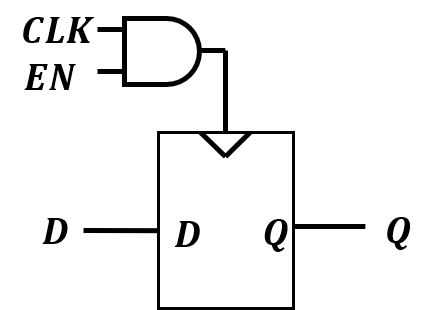
如图是两种使能端的实现方式。看起来第二种方法要好，但实际上第一种方法更优。因为第二种方法会影响CLK工作（不同的与门所需时间不同），可能导致原本的同步电路变成异步电路（如上面的寄存器）
带复位或置位功能的触发器
当复位为1时，触发器被置0, 复位为0时不影响电路正常工作。
复位分为两种形式：
- 同步复位： 只在上升沿复位
- 异步复位： 只要reset位置1就进行复位
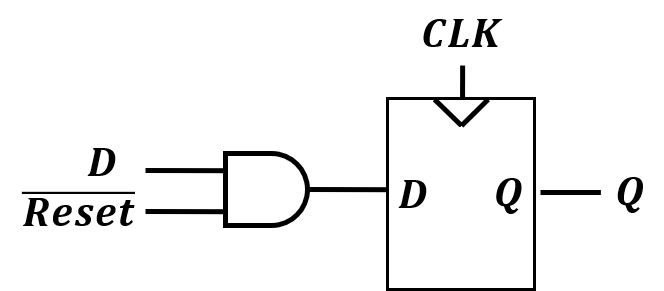
如图是一种同步复位的实现方式。
而置位就是将触发器置为1，和复位大致相同。
门控时钟
在电路中时钟网络占据了大量的功耗，而利用门控时钟可以将时钟关掉从而降低功耗。
最直接的方式是将时钟与使能相与，然而由于en会产生毛刺，从而导致GCLK产生毛刺，这会导致寄存器的时序紊乱
因此可以通过锁存器锁存en信号
需要注意的是锁存器的时钟和原时钟是相反的，图中存在非门符号。如果二者时钟相同，那么假设clk为高电平时en为高，此时锁存器的输出为高，GCLK也为高，而单clk转为低电平后，GCLK为低，这样使得GCLK多了一段高电平的时间，如下图所示CgAnd为GCLK 
锁存门控的缺点：
- 如果在电路中，锁存器和门距离较远，那么锁存器时钟和门时钟偏移较大，仍然可能出现毛刺
- 如果时钟使能信号和锁存器太近，将会不满足建立时间
或门门控
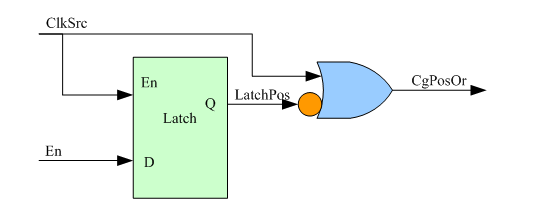
如果en为低电平，此时clk输出始终为高电平，而当clk为低电平时en为高，那么便会导致错误。因此推荐时钟上升沿有效使用AND门，下降沿有效使用OR门。
同步时序电路
同步时序电路中有一个时钟输入，时钟的上升沿表示电路发生改变的时间。当前状态称为现态，下一个状态称为次态。
同步时序电路的组成规则
- 电路中的模块是寄存器或组合逻辑电路
- 模块中至少包含一个寄存器
- 所有寄存器都共用一个信号
- 电路的每个环路都至少包含一个寄存器
例如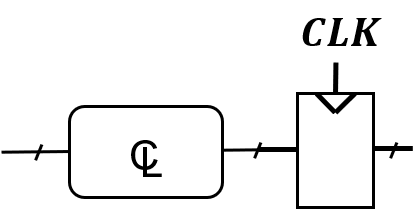
是同步时序电路，而
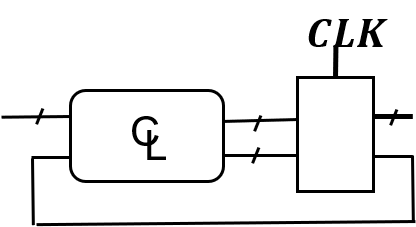不是时序逻辑电路，因为它是锁存器不是触发器
两种常见的同步时序电路： 有限状态机和流水线
有限状态机
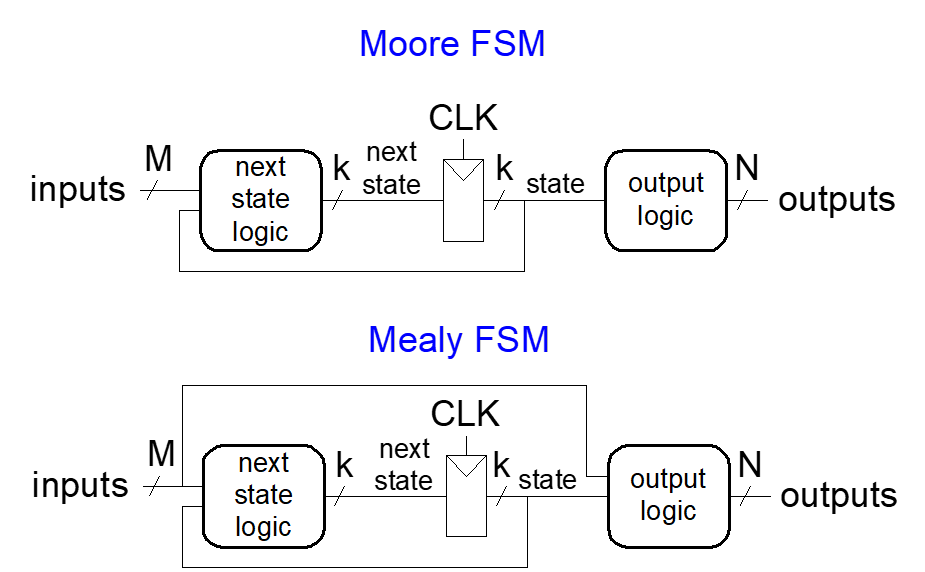
这两种有限状态机都受时钟信号的控制，寄存器前面是用来决定下一个状态的，它由输入和当前状态共同决定。而触发器后面就是处理信号模块。
moore机的输出信号不由输入信号直接决定，并且它只有在时钟上升沿才会发生改变。
mealy机的输出信号直接由输入信号决定，并且它在任意时刻输出都有可能改变。
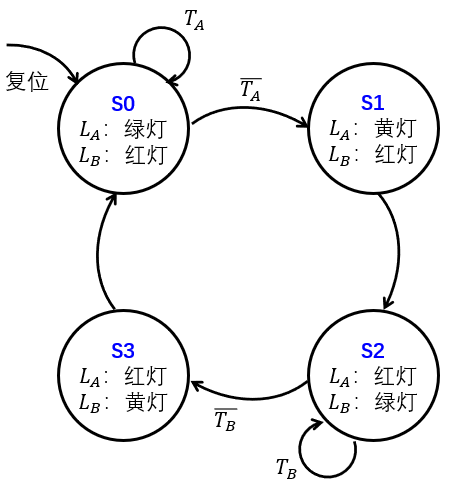
例如： 交通信号灯的设计
输入： 两个交通传感器 $T_A , T_B$.当有人经过时返回True
输出，两个交通信号灯$L_A , L_B$.他们都有红绿黄三种状态
有一个5s的时钟，当时钟到达时，根据传感器的情况进行改变。此外还有一个复位键。
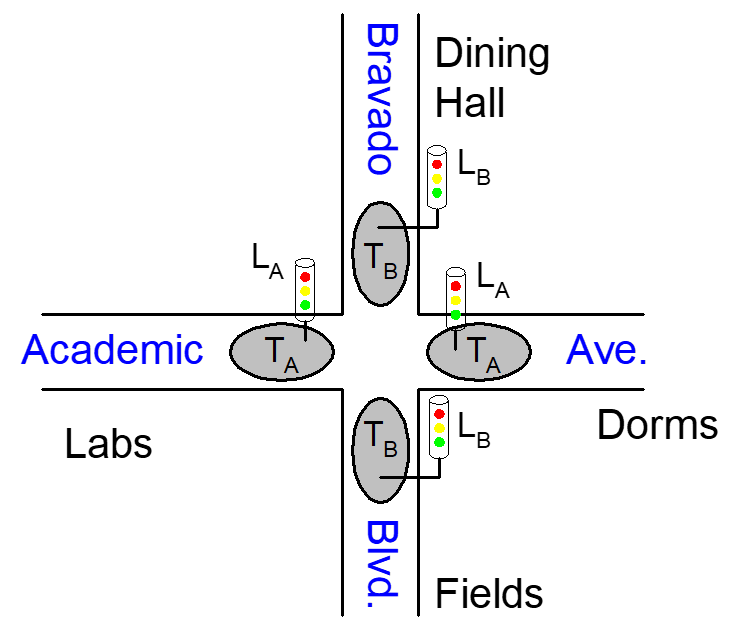
- 画状态转换图.如果当前是绿灯并且有行人通过不做改变，如果没有行人通过就变成黄灯，5s后变成红灯
- 画出状态转换图纸后，将其转换为状态转换表
| 现态 | 输入 | 次态 | |||
| S1 | S0 | Ta | Tb | S1' | S0' |
| 0 | 0 | 0 | x | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 0 |
| 0 | 1 | x | x | 1 | 0 |
| 1 | 0 | x | 0 | 1 | 1 |
| 1 | 0 | x | 1 | 1 | 0 |
| 1 | 1 | x | x | 0 | 0 |
我们认为00是S0状态，01是S1状态，以此类推。也就是说四种状态需要两个二进制位，需要两个触发器。
同理，我们可以画出输出的状态转换表
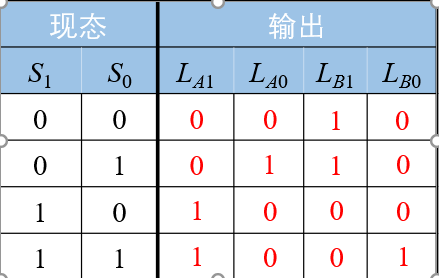
由于输出有红绿黄三种状态，所以同样需要两位输出表示状态。用00表示绿，01表示黄，10表示红。
- 化简
当我们把真值表画出来后，就可以用卡诺图或者直接进行化简了。
例2：
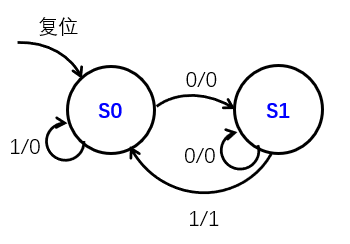
一个蜗牛在一条写满0和1的纸带上爬行。当它爬过的最后两位是01时，蜗牛会对着你微笑。请设计一个Mealy型状态机来模拟蜗牛的行为。
- 状态转换图
除号左边是当前输入，右边是输出。例如在状态S0时输入0，输出为0，如果输入一直是0那么转到状态S1.
从电路导出状态机
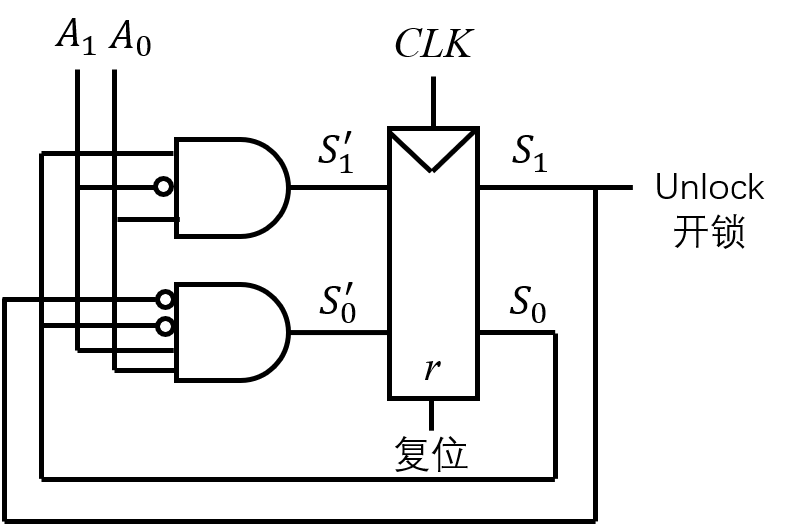
上图是一个开锁器的电路，我们需要根据这个电路导出状态转换图。
- 首先得出次态方程和输出方程：
- 之后根据方程写出状态转换表
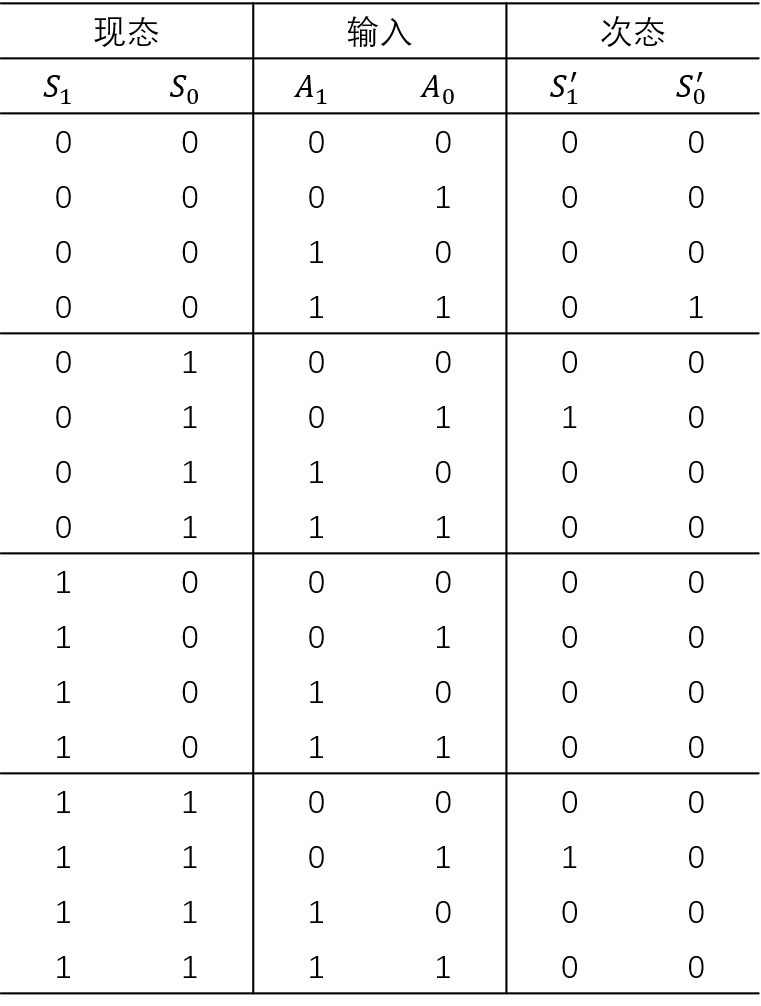
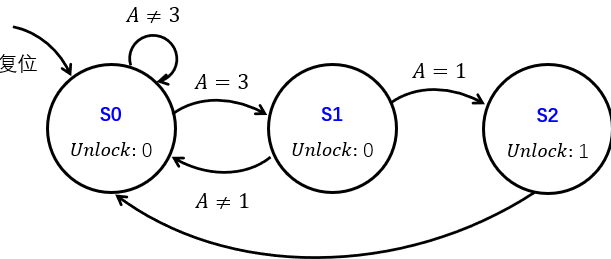
可以看到其他三个状态中没有任何一个次态会转到11，也就是11状态不可达，因此可以直接把11状态删去
因此一共有三个状态00， 01， 10,然后根据状态转换表在这三种状态中进行转换即可
静态时序分析
静态时序分析主要验证系统间的路径是否满足给出的时序约束。他不需要产生测试向量验证电路功能，并且只能应用于同步电路
时序分析模型
时钟的时序特性分别为时钟周期（clock period)、时钟占空比（clock duty cycle）、时钟转换时间（clock transition time）、时钟延迟（clock latency）、时钟偏斜（clock skew）、时钟抖动（clock jitter）
时钟抖动是同一个时钟的两个时钟周期存在偏差，它是由晶振本身特性，电源及温度变化导致的。而时钟偏移是同一个时钟产生的多个子时钟信号之间产生延时，也就是时钟信号到达不同寄存器的时间不同导致的偏移。
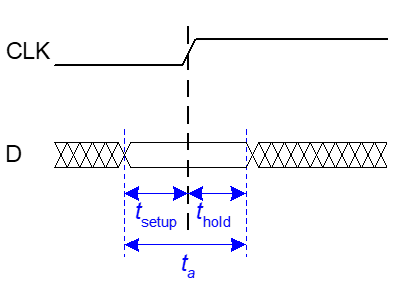
在时钟信号到来时有一段时间内输入信号是不可以改变的，贸然改变可能会导致如前面那样的不稳定状态。
- 建立时间： 在时钟信号到来前输入信号需要稳定的时间
- 保持时间： 在时钟信号(采样沿)到来后需要保持稳定的时间。
- 孔径时间： 也就是总的需要保持稳定的时间，等于建立时间+保持时间
- 最小延迟($t_{ccq}$)： 在时钟有效沿到达后后面的器件开始改变的最小时间
- 传播延迟($t_{pcq}$)： 改变的最大时间
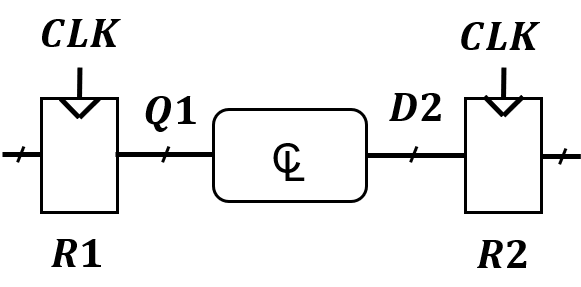
- $T_{D}$: 寄存器的数据稳定时间
- $T_{clk1}$: 时钟源到第一个寄存器所需时间
- $T_{Comb}$: 组合逻辑所需时间
寄存器2采样沿到达时间：
数据到达时间:
第二次数据到来时间:
建立时间余量：
hold time是指数据在clk2触发之后仍需保持不变的时间，也就是下一次数据经过组合逻辑到达触发器2的时间
保持时间余量：
建立时间和保持时间受工艺限制而固定，计算出的余量需要大于规定的建立时间和保持时间才可以认为没有时序违例。
其中保持时间余量的公式中没有时钟周期，并且越长的组合逻辑越不容易发生违例。
建立时间和保持时间是同步时序电路中的要求，而恢复时间(recovery time)和去除时间(removal time) 是对于异步时序的要求。
- 恢复时间： 类比建立时间，指明当前异步信号生效之后触发器恢复正常所需的最少时间
- 去除时间： 类比保持时间，在有效时钟沿之后最短使异步控制信号去除的时间
分析方式
- pre-layout: 早期验证时使用，它使用综合网表、约束文件（SDC）、工艺库、线负载模型作为输入，输出时序报告与关键路径分析。他假设时钟树是理想的（零延迟），因此这种分析方式会造成一些误差
- post-layout: 它使用post-layout网表（包含物理位置信息）、寄生参数文件（SPEF）、SDC和工艺库。它会输出精确的时序报告，必须要通过post-layout才可以流片。
时序命令
以下给出一些和时序相关的命令
时钟定义：
- create_clock: 定义一个时钟，需要给出时钟源、周期、占空比和边沿时间。例如
create_clock -name CLK -period 20 -waveform {0 5} [get_ports clk]，这个时钟的时钟周期为20ns,其中{0, 5}为上升沿 - create_generate_clock: 定义衍生时钟（分频时钟）
- set_clock_uncertainty: 指定时钟的不确定度。可以使电路的时序更加严苛，保证稳健性
时钟不确定性来源于
时钟偏差(clock skew): 时钟源到不同触发器之间的偏差
时钟抖动(clock jitter): 时钟边沿的超前或滞后
时钟延迟(clock delay): 网络延迟和源延迟,源延迟是从时钟源到时钟定义点（create_clock)之间的延迟
例如set_clock_uncertainty -setup 0.2 [get_clocks CLK] - set_clock_latency: 设置时钟延迟，例如
set_clock_latency 0.8 [get_clocks CLK]
- setinput_delay: 设置$T{D}+T_{Comb}$的稳定时间,
set_input_delay -clock CLK -max 6 [get_ports D2] - setoutput_delay: 设置$t{setup}$和$t_{hold}$, min是hold时间。`set_output_delay -clock CLK -min -0.2 [get_ports OUTC]
- set_multicycle_path: 确定这条组合逻辑需要多个周期才能完成，虽然每个周期还会进行采样，但是时序分析时采用多周期进行采样。
set_multicycle_path 2 -hold -from {get_pins UFF0/Q} -to {get_pins UFF1/D} - set_half_path
- set_false_path: 不进行时序分析，一般异步电路不需要时序分析
异步时序
同步时序电路： 所有触发器的时钟使用同一个时钟脉冲源。分频时钟也属于同步时序，即使相位不同，由于相位差固定仍可以进行同步。
异步时序电路： 电路中至少有两个没有固定相位关系的时钟源，两个晶振就属于两个固定相位不同的时钟源。并且异步时序中还可以使用不带时钟的触发器作为存储。
同步时序电路的优势：
- 同步时序电路较为容易的使用寄存器的复位端，使得电路有一个确定的初始状态
- 同步电路可以避免受温度、电压、工艺的影响，消除毛刺，使得设计稳定
- 容易组织流水线，提供芯片运行速度
- 可以使用静态分析工具进行分析
异步设计的优势：
- 无时钟偏移问题： 异步电路使用大量的本地时序控制信号取代整体时钟
- 低电源消耗： 仅在需要时才消耗能量
- 好的电磁兼容性
- 模块化特性突出
亚稳态
触发器需要满足其规定的建立时间和保持时间，否则结果是不可预知的，即亚稳态
在异步时序中亚稳态是一个不可避免的问题，触发器平均触发亚稳态的时间可以使用MTBF（mean time between failures）描述
其中：
- $t_{\tau}$:分辨时间
- $\tau , T_0$: 常数
- $f$: 时钟频率
- a：异步事件触发频率
改善亚稳态的措施：
- 使用更快的寄存器，减少建立保持时间
- 使用同步机制，防止亚稳态传播
- 降低采样时钟频率（根据MTBF公式）
- 改善时钟质量，用边沿变化快速的时钟信号
单比特同步策略
为了降低亚稳态发生的概率，可以使用双锁存器
如图所示，假设寄存器1恰好在clk2上升沿时状态改变，那么寄存器2将会进入亚稳态，而亚稳态会在一段时间后稳定为某一随机状态，因此寄存器3没有进入亚稳态。因此这种方式只是保证同步后不发生亚稳态，而无法保证同步之后数据的正确性。
这里为了降低发生亚稳态的概率，首先需要将sig1寄存一周期。如果直接将sig1连接寄存器2，由于sig1运算时的组合逻辑会产生毛刺，而这些毛刺可能会被寄存器2采样从而导致亚稳态
上面的方式适合慢时钟域同步到快时钟域（1.5倍以上），如果是快时钟域同步到慢时钟域可能会发生漏采
解决方案
对于多比特的信号，一个简单的方式是将每一个比特按照单比特信号处理，然而实际上这些信号直接由于连线和时钟偏移（skew）等问题会导致信号输出不同步，从而导致跨时钟域时信号错位。
针对这些信号要尽可能的在跨时钟域之前进行处理，合并为单比特信号。或者只传输一个信号，然后在a时钟域再进行处理。不能直接传输两个信号
如果确实需要传输多比特的数据，那么可以使用多周期路径规划或异步FIFO
多周期路径规划
脉冲同步法（开环结绳法）
首先目的是将一个时钟域的数据同步到另一个时钟域。而为了实现这个目标，额外添加一个脉冲（使能）信号来控制。
工作步骤：
- 当发送时钟域使能（脉冲）到来时，数据（Data In）可以通过寄存器，并且将一周期的脉冲变成多周期的高电平
- 电平信号经过三级同步后在接收时钟域检测脉冲
- 检测到脉冲则使能输出寄存器得到Data Out
脉冲的时间间隔至少要大于接收时钟域的两个周期（根据输出脉冲所需周期决定），否则将会导致输入的数据被冲刷
发送时钟域的脉冲-电平转换（结绳 toggle）逻辑：
logic enable; |
接收时钟域将电平转换为脉冲的逻辑：
logic en_o; |
闭环结绳法
它和之前的结构相比增加了aready来进行反馈。
当脉冲信号通过结绳结绳转换为接收时钟域的脉冲，再将其传递给发送时钟域通过边沿采样转换为脉冲，这样发送时钟域就能知道使能信号已经传递。
然而上面这种方式的b_ack也是单周期脉冲，如果发送时钟域较慢可能无法采集，因此为了适配快采慢，可以使用下面的结构
这样添加了一个bload信号，只有当确定b接收之后才会发送ack信号给a，并且使用电平信号，避免了b_ack漏采的问题
异步FIFO
异步FIFO的读与写在不同的时钟域，他的实现使用双端口RAM，包含一个读指针和一个写指针，当FIFO未满时可以写入，当FIFO未空时读取。
读写指针编码
读写指针最简单的编码方式是使用二进制码，判断空满时需要将读写指针同步到一个时钟域中。然而读写地址包含多个比特，这就涉及多比特同步问题，可以参考上面的实现方式，实现复杂且速度并不理想。
因此读写指针可以采用格雷码（gray)进行编码。格雷码相邻数据之间只相差一位，因此可以使用单比特同步策略进行同步。
格雷码可以使用对称轴构造
先镜像翻转，再左边最高位补0，右边补1 |
格雷码和二进制码转换
module gray_to_binary #( |
假设快时钟域同步到慢时钟域，那么快时钟域的指针同步时可能会改变多次。但是此时并不需要多比特同步，因为多比特同步实际上处理的是本因同步的信号在跨时钟域后没有同步的问题。而快时钟域的指针改变时一次只会改变一位，当慢时钟域采样沿到来时不会出现有两个比特需要改变而其中一个未改变完成的问题。
如果在同步时出现了亚稳态，那么也只可能发生应该改变的指针同步后没有发生改变，并不会导致空满信号判断错误。
空满信号生成
当读写指针相同时，此时FIFO可能为空也可能为满，因此读写指针头部需要补上一位。
例如假设FIFO包含四项，读写指针初始值均为0，现不断往里填入数据。当写指针为3’b100，读指针为3‘b000，因此当最高位不同，其他位相同时为满。
而在格雷码中当最高位与次高位不同，其他位相同时为满。
其次判断满信号需要将读指针同步到写时钟域中判断，而判断空信号需要将写指针同步到读时钟域中判断
由于读写指针需要进行同步，因此会导致判断空满信号时会产生延迟。假设将写指针同步到读时钟域判断满信号，假设在a周期已经满了，然后写指针还需要经过两周期同步才能生成满信号，在这两周期内如果有写入会导致溢出。而空信号同理，将写指针同步到读时钟域时即使中途有写入，只会导致读取延迟几周期，而不会产生溢出的错误。
FIFO深度计算
例一： 设计一个异步FIFO用于数据缓存，FIFO写入数据时钟100MHz，读出时钟50MHz，写入数据在100Cycle最多写入50个数据，那么FIFO深度设计多少合适
首先假设两个100周期，第一段后50个周期和第二段前50个周期都在写入数据，那么也就是说100个周期内会连续写入100个数据，而读出数据时钟为写入时钟的1/2，因此这段时间内只能读出50个数据，因此FIFO至少为50.
例二： 假设写入时钟为50MHz，读取时钟为20MHz，突发数据长度为100。
公式： FIFO_DEPTH >= Burst length - (Burst length * rd_clk / wr_clk)
即写入时需要考虑读出的数目，本题写入100个会读出40个，因此深度为60
DMUX同步器
针对带有数据有效标识信号的多比特数据，并且多比特数据需要保持一段时间。
DMUX针对数据有效信号进行同步，需要注意的是如果是快时钟域到慢时钟域需要替换图中红色部分。
时序逻辑建模(always_ff)
always过程块的结构如下always list)
statements;
always_ff用来表示触发器，例如：module flop ( input logic clk,
input logic [3:0] d,
output logic [3:0] q);
always_ff @(posedge clk)
q <= d;
endmodule
它的输出为：
可以看到，通过这种建模结果会有寄存器出现。
- posedge: 表示这个变量会在上升沿触发
- <=: 非阻塞性赋值，也就是说这些语句都是并发的，会一起执行。这就需要通过寄存器进行同步了，例如下面这个例子
module syncgood( input logic clk, |
输出为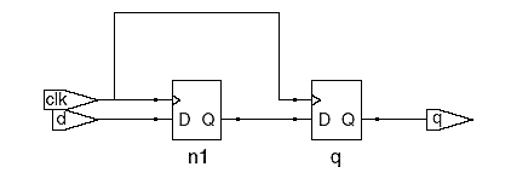
我们可以把它当成一个次态方程，每一次触发时右边的值都会同步的赋值给左边的值。
而如果不使用非阻塞性赋值module syncbad(input logic clk,
input logic d,
output logic q);
logic n1;
always_ff @(posedge clk) begin
n1 = d; // 阻塞赋值
q = n1; // 阻塞赋值
end
endmodule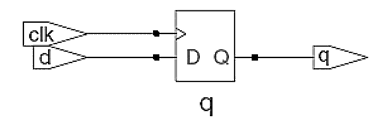
我们也可以添加reset位module flopr ( input logic clk,
input logic reset,
input logic [3:0] d,
output logic [3:0] q);
always_ff @(posedge clk)
if (reset) q <= 4'b0;//同步复位
else q <= d;
endmodule
module flopr ( input logic clk,
input logic reset,
input logic [3:0] d,
output logic [3:0] q);
always_ff @(posedge clk, posedge reset)//异步复位
if (reset) q <= 4'b0;
else q <= d;
endmodule
时序逻辑建模的应用
移位计数器
功能：在每一个时钟内，每一个寄存器的内容都向右移动一位，最前面的位移入$S_{out}$
作用： 可以把并行变成串行，可以用在网络传输中。
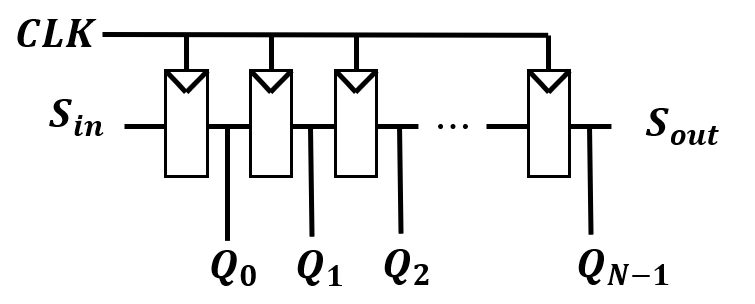
我们可以对他稍作改进，可以一次性输入这么多位
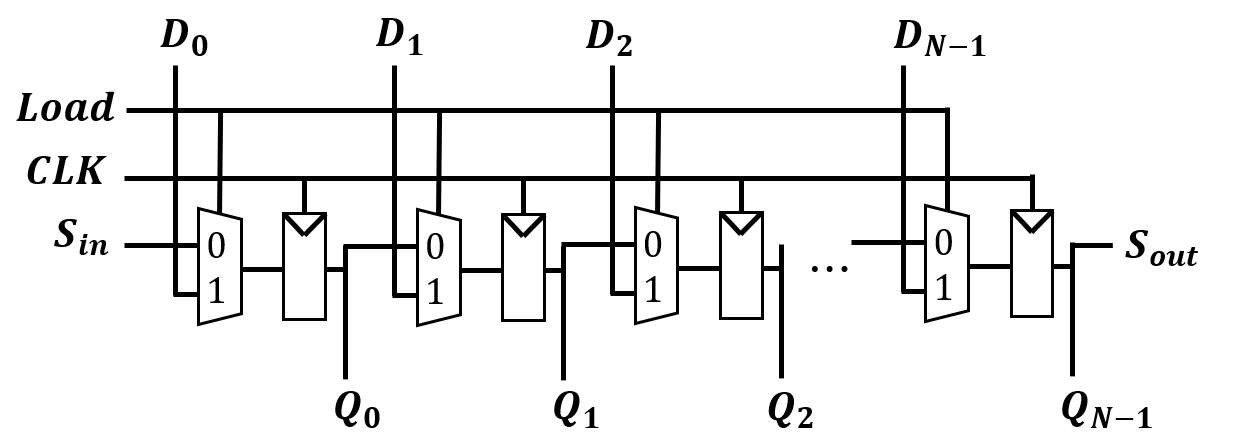
$D0 , D_1 , … , D{N-1}$是输入，而Load决定是否需要输入。每过一个时钟周期所有寄存器都会接受前一个的输入。建模语句为：
module shiftreg #(parameter N=8) |
有限状态机的建模
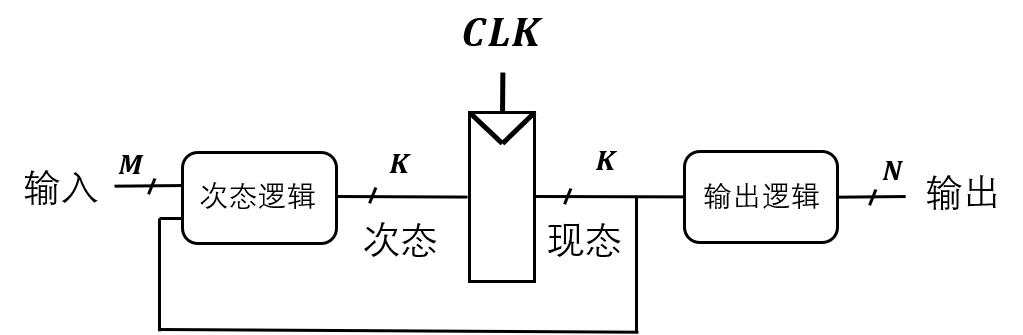
这是一个典型的moore型状态机，它的建模语句为module divideby3FSM ( input logic clk,
input logic reset,
output logic q);
typedef enum logic [1:0] {S0, S1, S2} statetype;
statetype [1:0] state, nextstate;
// 寄存器
always_ff @ (posedge clk, posedge reset)
if (reset) state <= S0;
else state <= nextstate;
// 次态逻辑
always_comb
case (state)
S0: nextstate = S1;
S1: nextstate = S2;
S2: nextstate = S0;
default: nextstate = S0;
endcase
// 输出逻辑
assign q = (state == S0);
endmodule
输出逻辑和寄存器并列是因为输出是时时刻刻受到寄存器的输出影响的，只要寄存器输出改变，他就会改变
存储器阵列
Address是地址总线，有n位最多可以取$2^n$个数据。而Data是数据总线，表示一次可以取多少位数据。
例如Address=10, 那么我们可以取100，或者将101写入地址10处。
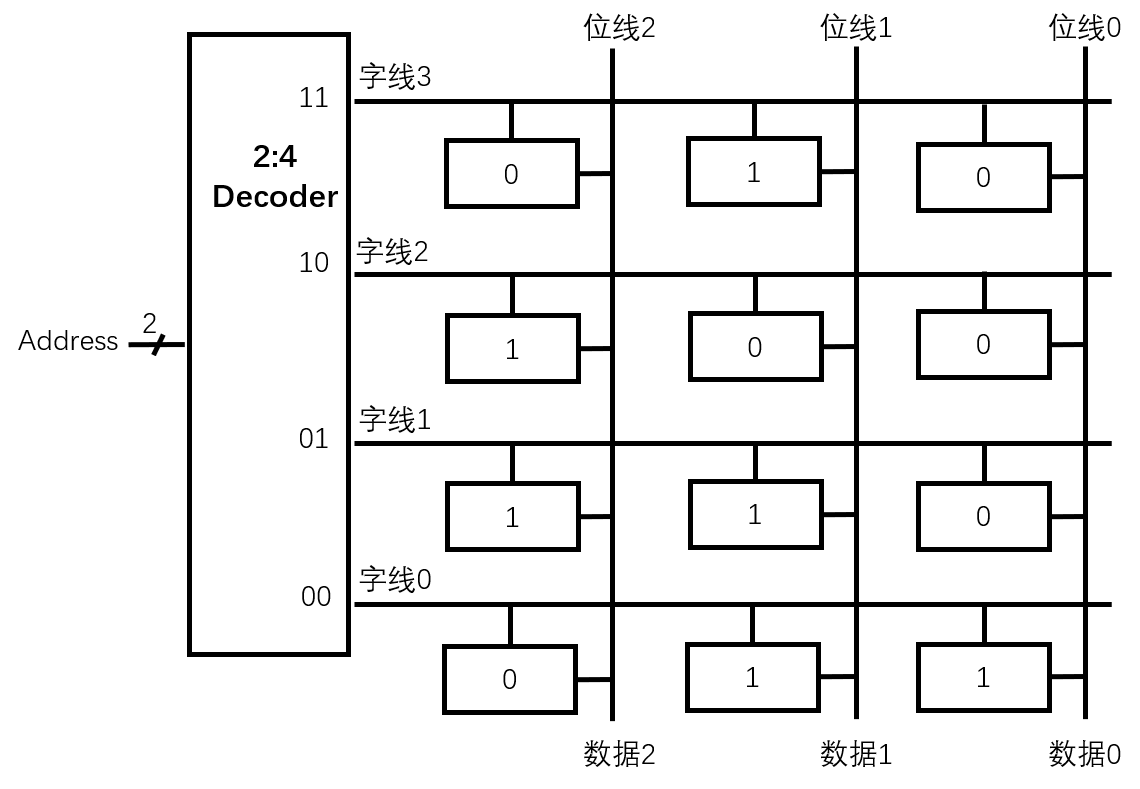
将上述逻辑展开就可以得到如图的结构了。其中字线如果为1就表示这条线可以读取或写入。其中每一个存储单元可以是DRAM存储单元或SRAM存储单元
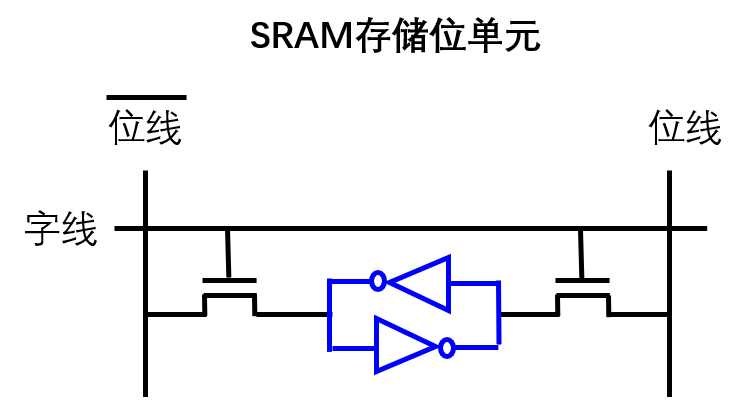 DRAM |
 SRAM |
此外，如果想要同时实现读写的功能，可以在数据接口处使用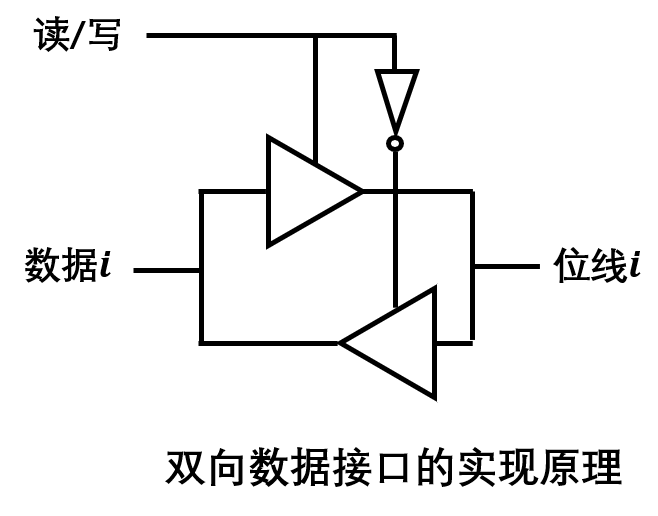
时钟分频
偶数分频将寄存器的输出的反向接入到输入端中可以实现二分频，然后以二分频的输出作为下一个寄存器的时钟可以做到4、8…分频。当然可以使用计数器调节至任意所需分频。
奇数分频如果不要求占空比为50%，可以利用计数器进行分频，此时占空比为M/N，N为所需分频，M为需要为高的周期数
如果必须要占空比为50%，那么可以通过将两个时钟通过&或|操作将占空比调节到50%
如图所示首先生成两个1/3分频时钟，并且CLK2在下降沿采样，此时二者相位差为1/6,然后将二者相或就可以生成占空比为50%的三分频时钟
线性反馈移位寄存器（LFSR）
如图所示，移位寄存器中移位之后会空出来一位，通过反馈函数将现有数据进行计算后填入$b_{n}$，那么数据便会持续变化，因此它经常作为伪随机数生成器。
LFSR中的数据可以只选取一部分参与运算，参与运算的位称为抽头。具体的运算可以表示为：
其中$c_{i}$表示该位是否参与运算，如果参与则为1。$\oplus$表示异或
它也可以对应特征多项式
图中的表达式为$f(x)=x^{4} + x^{3} + 1$