基础

分治法是将大问题分解成若干个小问题，通过解决小问题解决大问题的方法。它和递归关系密切。

大致流程

if(|P| <= n0) adhoc(p);
divide p into small k part;

for(int i=0; i<k; i++)
{
	yi = divide-and-conquer(pi);
    //递归解决各个子问题
}
return merge(y1,y2,...yk); 合并子问题的解

例题

找伪币

假如有十六个硬币，有一个是伪币，伪币比较轻，试用一个天平找出伪币

假如两两比较，最坏情况需要8次

如果使用分治法，需要四次。首先8个8个比较，然后在轻的一堆中比较。

计算a^n

如果使用 a a a…。那么复杂度是O(n).使用分治法，

a^n = a^(n/2) * a^(n/2) n%2 == 0

a^n = a^(n/2) a^(n/2) a n%2 == 1

所以 T(n) = T(n/2) + 0(1)

其中T(n/2)是计算a^(n/2)所需要的时间， O(1)是两个数相乘需要的时间。由主定理可得，复杂度是 O(logn)。

可以看到，通过分治法，有时我们可以减少一些重复运算。

大整数乘法

两个大整数乘法直接相乘复杂度是O(n^2)（注意这里指的是每个bit相乘）

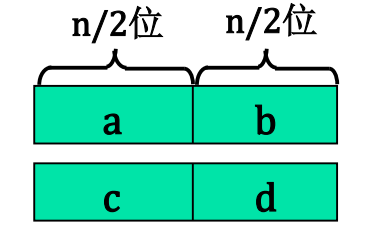
如果把它分成两个部分,如图所示，那么乘法就可以变成

(a* 2^(n/2) + b)(c * 2^(n/2) + d)
= ac * 2^n + (ad+bc) *2^(n/2) + bd

递推公式为 T(n) = 4*T(n/2) + 0(n)其中O(n)是ad和bc等两个分式相加的复杂度而不是计算2^n的复杂度。得到的复杂度为O(n^2)，没有改进。

但是如果写成 ac * 2^n +((a+b)(c+d)-ac-bd) * 2^(n/2) + bd则复杂度就变成了O(n^1.59)。

中间的中间问题

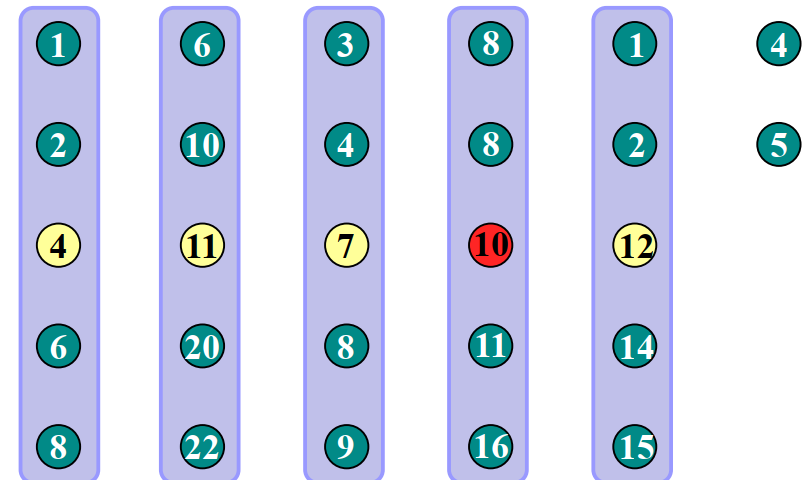
如图，对这些数进行排序。我们可以把这些数分成5组，然后每组找中位数。然后在所有的中位数中寻找中位数（中位数的中位数）。再用找到的中位数的中位数进行排序。

提出这个方法是因为快速排序在最坏情况下复杂度是$O(n^2)$，之所以可能是$O(n^2)$是因为可能我们每次选的支点都可能是最小值。而这个算法就是为了避免这种情况。

我们已经找到中位数的中位数了（图中是10，多余的两个数可以不管）。也就是说在10这组前面有两组。因为前面每组都有三个数一定比10小。那么一定有3n/10个数比10小。

假设有n个数，找到n/5个中位数，又找中位数的中位数，那么一定有n/10个数比中位数小（n/5个中位数中有一半比他小）。因为中位数前面两个数字也一定比他小，所以总共是3n/10。

可以证明找中位数的中位数时间复杂度是O(n)

最接近点对问题

问题：在二维平面上的n个点中，找出最接近的一对点

我们可以利用分治法进行求解。先用一个一条垂线将左右两边分隔开（一般选取中点），然后分别求左边最短距离和右边最短距离，然后比较这两个最短距离和中线两侧最短距离，找到最小值就是最接近的一组点。

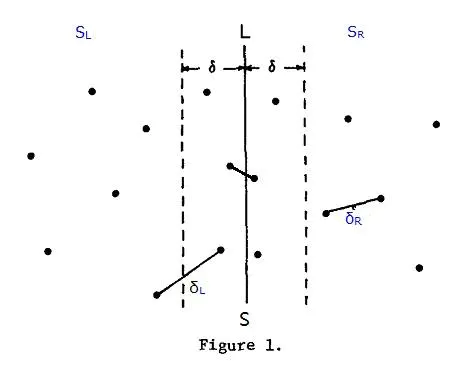
问题的关键在于怎么找中线两侧的最短距离。

$\delta = min{\deltaL, \deltaR}$,$\deltaL$是左边最短距离，$\deltaR$是右边最短距离。两侧最短距离一定要比$\delta$小的范围内考虑。

选取$L-\delta$到$L+delta$范围内的点，并且按照y值大小进行排序
选取左边的一个点(x, y), 对右边 $y-\delta \sim y+\delta$矩形范围内的点考虑。因为右边任意两个点的范围都大于$\delta$,因此可以推断这个矩形中最多不超过六个点。也就是说只需要检查$6*\frac{n}{2}$个候选者。

它的复杂度是 T(n) = 2T(n/2) + O(n).用主定理解得复杂度为O(nlogn)