下界Ω 上界O 紧界Θ

这几个界都是由极限得来的。

上界： 对于 任意正常量c>0,都存在No>=n,使得 0<=f(n)<= cg(n).则可用 f(n) = O(g(n))表示。

g(n)一般使用简单的式子如 n nlogn, $n^2$,…

这个式子其实就是极限的表达形式，所以我们也可以用极限的形式表达：

下界： f(n)>=cg(n)

紧界： f(n)= cg(n)

分析递归式的复杂度

之所以递归式要单独拿出来分析是因为递归式很难从直观上去判断。例如 f(n) = f(n-1)+f(n-2).这个递归式如果要分析的话可以写成 f(n) = f(n-1) + f(n-2) + 1，最后一个1表示每一层需要进行的运算，因为这里只有一个加法运算，所以是加1.

代入法求递归式

代入法就是首先猜测复杂度，然后用归纳法证明。

例如： T(n) = 4T(n/2) + n

假设 T(n) <= cn^3

当n = 1时，可以找出一个足够大的c使，T(1) <= c， 成立
当n= k 时， T(k) <= ck^3
当n = n时， T(n) = 4T(n/2) + n <= 1/2 * c * n^3 + n >= cn^3，所以成立。

如果 T(n) <= cn^2

当n=n时， T(n) <= c * n^2 +n >= cn^2。 不成立

遇到这种与结果十分接近的式子时可以减去一个低阶项。

假设 T(n) <= c （n^2 - n)

当 n = n 时， T(n) <= cn^2 - c/2*n +n <= cn^2，成立

递归树法

递归树法是通过作图分析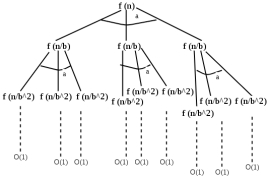

例如 f(n) = 2 * f(n/2) + n. 那么第二层是由两个f(n/2)组合而成 每个f(n/2)都会加上n/2,所以第一层和第二层都加上n。

总共有多少层呢？ 可以看到最后要减小到f(1)，而每次乘1/2,也就是 $n= 2^h$,h=logn.所以复杂度是 O(nlogn)（层数乘上每层数目）

拿一个跟复杂的例子。 f(n) = f(n/3) + f(2n/3) + n.对于这种我们通常使用夹紧准则获得一个近似值。例如一直从左边高度是log3 n ,右边是 log3/2 n.而右边到最后每一层不是n。这些差异我们可以忽略大致得到复杂度是nlogn。然后在用归纳法证明

主方法

对于 T(n) = aT(n/b) + f(n)

  1. 如果 f(n) = $O(n^{\log{b}{a} -\varepsilon}).也就是n^{\log{b}{a} -\varepsilon}$ 比 f(n)大，那么T(n) = Θ（$n^{\log_{b}{a} -\varepsilon}$)
    这里e最好写出来

  2. 如果f(n) = $n^{\log{b}{a}}$, 那么 T(n) = Θ $(n^{\log{b}{a}}\log_{}{n})$

  3. f(n) = Ω($n^{\log_{b}{a+\varepsilon}}$),还要满足存在c<1和足够大的n使$\quad af(\frac{n}{b}) <="cf(n)$,则" t(n)="Θ</math>(f(n))

要注意，case1 和 case2之间有空隙，case2和case3之间有空隙。一个例子是

T(n) = 2T(n/2) + O(nlogn)

这个$n^{\log{b}{a}}$的确比nlogn小，但是 $\frac{nlogn}{n} = logn$都渐进小于 $n^{\varepsilon}$（也就是对任意$\varepsilon > 0 \quad \lim{n \to \infty} \frac{logn}{n^{\varepsilon}}=0$ ）,所以这是渐进大于而不是多项式大于，不能用case3.

2情况的拓展形式

f(n) = $n^{\log{b}{a}} \log{}{n^x}$

则 T(n) = Θ $(n^{\log{b}{a}}\log{}{n^{x+1}})$