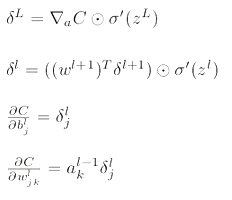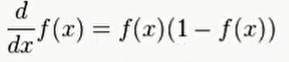多层向前神经网络

该神经网络的层数大的有三层：输入层， 隐藏层（隐藏层可以有多层）， 输出层。

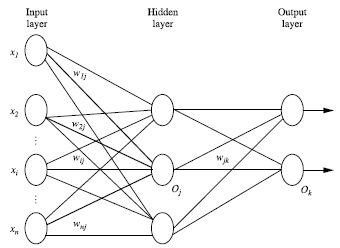该图是两层神经网络（输入层不算）

每层由单元组成（例如决策树算法中的一和零） 。输入层就是传入一些特征向量。

理解：

下一层的神经元可以看成y，然后每个w可以看成k，那么其实就是一条直线。有些层次用来做 && 或 || 的操作，这样就可以用多条直线对区域进行划分.

权重： 每两层有线进行连接，线上的数值就是权重，我们是通过特征向量和权重相乘求和再用非线性方程转化得到下一层的

3. 设计神经网络结构
     3.1 使用神经网络训练数据之前，必须确定神经网络的层数，以及每层单元的个数
     3.2 特征向量在被传入输入层时通常被先标准化(normalize）到0和1之间 （为了加速学习过程）
     3.3 离散型变量可以被编码成每一个输入单元对应一个特征值可能赋的值
          比如：特征值A可能取三个值（a0, a1, a2), 可以使用3个输入单元来代表A。
                    如果A=a0, 那么代表a0的单元值就取1, 其他取0；
                    如果A=a1, 那么代表a1de单元值就取1，其他取0，以此类推

     3.4 神经网络即可以用来做分类(classification）问题，也可以解决回归(regression)问题
          3.4.1 对于分类问题，如果是2类，可以用一个输出单元表示（0和1分别代表2类,例如黑和白，不是黑就是白，所以只需要输出一类）
                   如果多于2类，每一个类别用一个输出单元表示
                   所以输入层的单元数量通常等于类别的数量

          3.4.2 没有明确的规则来设计最好有多少个隐藏层
                    3.4.2.1 根据实验测试和误差，以及准确度来实验并改进

交叉验证方法

这是一种验证正确率的方法。例如我们把样例集分成10份，第一次用第一份做测试集，其他做训练集，第二次用第二个做测试集，其他做训练集。这样做十次得到的正确率再求平均值。当然划分不一定是十份。

神经网络训练大致过程： 先根据输入确定结果，通过预测结果和真实结果之间的误差反推更新权重。

开始的时候可以随机的在1到-1之间给权重

下面这个式子就是从下一层的计算公式，单元值乘以权重求和然后再加上偏向(oj)

前面到Bias的部分已经提到了，就是上面那个方程，最后还需要经过一个非线性函数（激活函数）。

激活函数：

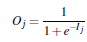
其中Ij就是前面提到的函数。

之后反向更新权重：

对于输出层：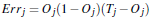
Tj是输出层标签真实值

对于隐藏层：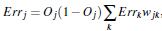
其中Errk是前面一层的误差

权重更新：

l是学习率（learning weight），这是我们手工设置的值，在零到一之间

偏向更新：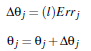
upload successful

终止条件：

  • 权重的更新低于某个阈值
  • 预测的错误率低于某个阈值
  • 达到预设一定的循环次数

梯度下降算法

数学中梯度指的是函数关于各个偏导的一个向量，它的意义是指向上升最快的方向。因此负梯度就是下降最快的方向。

梯度下降算法的基本思想就是沿着梯度每次走一定距离，然后再次计算梯度，重复步骤直到走到最低点。这里的最低点是极值而不是最值

以二维为例。如果让x在最低点左边。x-梯度（导数），那么x增大，朝着最低点靠近。如果在右边x-梯度，x减小，同样朝着最低点靠近。

我们是根据loss function来对神经网络进行调整的。而lossfunction的参数就是w和bias，因此可以对w和bias求偏导然后w- 偏导对w进行修正。

随机梯度下降算法： 多次随机选取一些样本（mini-batch)，直到所有样例都被选取。

反向更新

反向更新利用了梯度下降算法。也就是使用 w = wi - (delta)w的方式进行更新。

(delta)w = L * 偏Cost / 偏w ， 所以我们的目标就是要求出偏导。

反向更新主要用到了四个式子。

这几个式子都有证明，这里不详细描述。

  • 第三个和第四个式子就是偏导，我们看到其中的量可以通过第一个和第二个方程求出来。
  • 第一个式子是对于输出层来说的。右边第一项指的是cost关于a（预测值）的偏导。这里cost的计算式为 (预测值-实际值)的平方求和再除以2n。因此偏导就是预测值减去实际值。后面一项是激活函数的导数。
  • 第二个式子是对于其他层。

这里还有另一种cost

它的偏导数为 .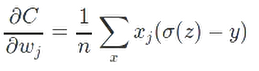

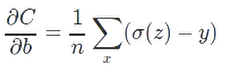
这个偏导数好在偏导的大小由a-y决定。a-y其实就是error。 error大，下降就要快。

推导过程

其实反向更新就是求偏导
这张图表示的是从输出反向推第一个权重，也就是上面的第一个式子。

net = w * x + b
out = 1 / 1 + e^(-net)
∂E / ∂out = target - out
∂out / ∂net = net * (1 - net)
∂net / ∂w = x
∂E / ∂w = (target - out) * net * (1 - net) * x

再看另一个例子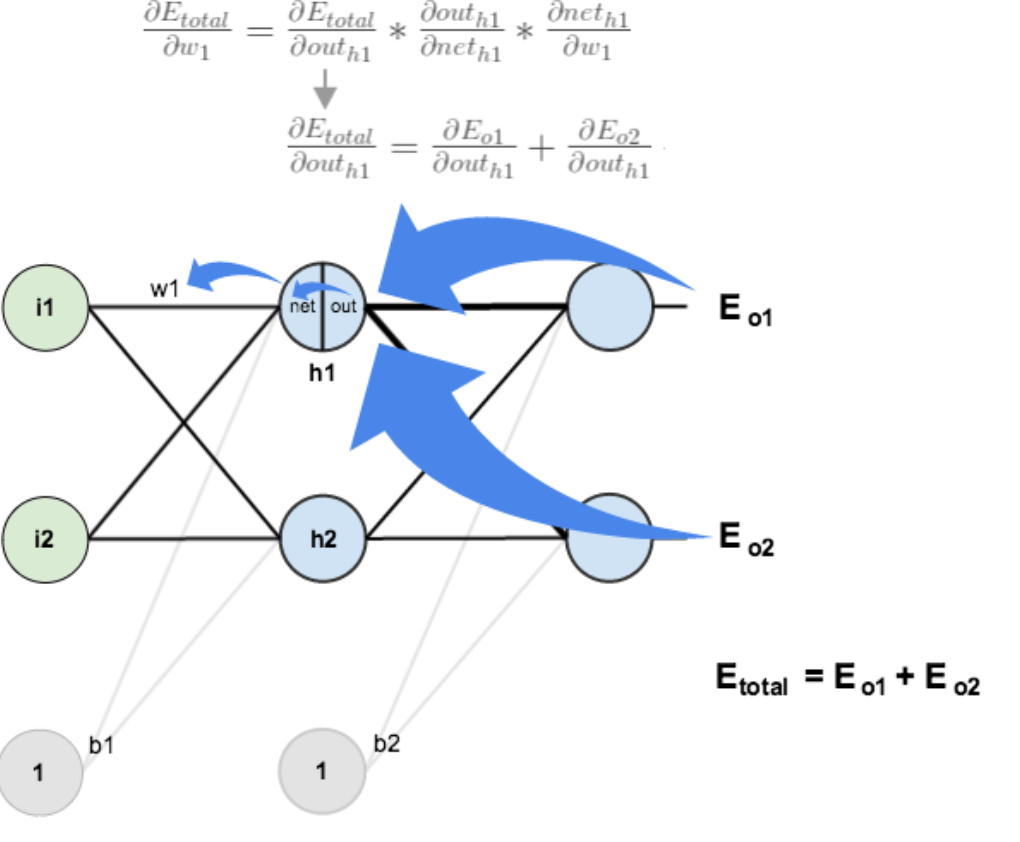这里就可以解释为什么有个求和的过程了，到w不只有一条路，而这里多了两个偏导∂outh1 / ∂neth1 和 ∂neth1 / ∂w1.这里的数值和前面是一样的。

有一点和前面不同，前面是∂E / ∂w，这里是∂E / ∂outh1。所以前面最后乘了一个x而这里乘了一个w。

非线性转化函数

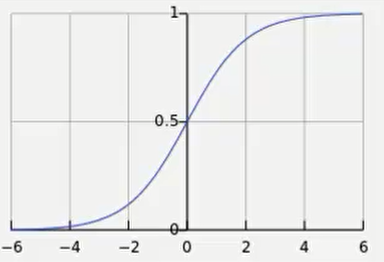
激活函数一般使用S型曲线（sigmoid）。一般是双曲函数(tanh)或逻辑函数。

广义上的sigmoid函数需要在-1到1之间变化并且平滑。

双曲函数：

tanhx = sinhx/coshx =

sinhx = (e^x - e^(-x))/2 、 coshx = (e^x + e^(-x)) / 2

导数：

图像为：

逻辑函数

p(t) = 1/(1 + e^(-t))

导数：

图像为：

减小overfitting

  1. 增加训练数据集
  2. 减神经网络的规模

  3. regularization .这是一个例子，后面一项也可以应用于其他cost函数中。加了这一项后神经网络会倾向于学习较小的权重,更少可能受到局部噪音影响
    w的更新也有变化
    nameda随着n的变化而变化，目的是不让比值太小从而使作用失效

    另一种regularization函数 它的偏导数为注意当w=0时，w不可导，所以直接使用没有regularization的。

    1. DropOut： 防止过拟合。具体方法时让需要dropout的层的百分之p的神经元关闭（即让需要关闭的神经元值为0）。然后多次随机剔除，最后再把权重除以p
  5. softmax

这个函数有一些独特的性质。例如zj增大，那么对应输出增大，其他输出减小。并且同一层所有输出值的和一定是1，可以用来模拟概率。所以经常用在输出层当做概率

对应我们可以定义一个新的cost函数 Cost(p,q)=−∑xp(x)logq(x)， 其中p是真实值，q是估计值. 它的偏导为这个偏导和上面的cross-entropy类似。

卷积神经网络

卷积神经网络对隐藏层进行了细分，常用于对图像处理。

  • input layer： 还需要对输入数据进行一些处理，如减去均值（只需要使用训练集上均值，测试集也是使用训练集均值）
  • 卷积计算层（CONV layer）： 通过一个窗口进行移动然后再和w矩阵进行点乘过滤一些信息。有三个主要参数，深度，步长和填充值。深度指的是下一层神经元数目，步长指的是窗口一次移动的长度，填充值是为了防止移动超出范围在周围补的一圈零。

这里深度是2，步长是2，填充值是1.其中最右边绿色就是输出。它是通过左边蓝色的窗口和红色的w进行点乘然后相加得到的。有三层是因为输入一个32 32 3（RGB）的矩阵，然后通过运算可以得到输出矩阵。

  • 激励层： 将卷积层结果进行非线性映射，典型的激励函数是ReLu，sigmoid函数其实很少用了，因为在数据比较大的时候导数趋近于0，难以训练。

ReLu方程式 y = max(0, x).也就是小于0时y=0，大于0时y=x。但是这个函数问题是小于0时导数=0，也无法训练。因此改进是小于0时y=0.01x

  • 池化层（pooling layer): 池化层一般夹在连续的卷积层中间，它是用来压缩数据量，减少过拟合。方法是max pooling。也是通过一个窗口，每次去窗口中的最大值形成一个矩阵。

由原来的4 4矩阵变成2 2矩阵

  • 全连接层： 该层和前一层之间一般所有神经元都有权重连接，一般是放在神经网络尾部，是用来防止信息丢失太多的。

注意点

  1. 权重初始化： 使用高斯函数（正态分布）去随机初始化可以让权重随机化。也就是numpy.random.randn(in, out) / np.sqrt(in/2). in是输入层个数，out是输出层个数

  2. Batch Normalization: 它是用来减少初始值依赖的，通常在全连接层之后。具体算法其中y和b是神经网络自己学习的。

实现

通过前面逻辑函数的导数可以得知，前面权重更新其实就是运用激活函数的导数

import numpy as np


def tanh(x):
    return np.tanh(x)


def tanh_deriv(x): # 导数
    return 1.0 - np.tanh(x)*np.tanh(x)


def logistic(x):
    return 1/(1 + np.exp(-x))


def logistic_derivative(x): # 导数
    return logistic(x)*(1-logistic(x))


class NeuralNetwork:
    def __init__(self, layers, activation='tanh'):
        """
        :param layers: A list containing the number of units in each layer.
        Should be at least two values
        :param activation: The activation function to be used. Can be
        "logistic" or "tanh"
        """
        # layers是一个列表，代表输入层，隐藏层和输出层，列表中每个数字代表隐藏层中单元的数目，列表长度代表总共有多少层
        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_deriv

        self.weights = [] # 初始化一个列表来装所有的weight，这后来是一个三重矩阵
        for i in range(1, len(layers) - 1): # 随机初始化weight
            self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25) # 生成一个layers[i-1]+1行，layer[i]+1列的范围在-0.25到0.25的矩阵
            self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25) # 第i层到第i+1层之间

    def fit(self, X, y, learning_rate=0.2, epochs=10000):
    # epochs是训练次数（循环次数）
        X = np.atleast_2d(X)
        temp = np.ones([X.shape[0], X.shape[1]+1])# 初始化一个矩阵，值全是一，行数和列数由参数提供
        temp[:, 0:-1] = X  # adding the bias unit to the input layer
        X = temp
        y = np.array(y)

        for k in range(epochs):
            i = np.random.randint(X.shape[0])
            a = [X[i]]

            for l in range(len(self.weights)):  #going forward network, for each layer
                a.append(self.activation(np.dot(a[l], self.weights[l])))  #Computer the node value for each layer (O_i) using activation function
              #正向所有更新
            error = y[i] - a[-1]  #Computer the error at the top layer
            deltas = [error * self.activation_deriv(a[-1])] #For output layer, Err calculation (delta is updated error)

            #Staring backprobagation
            for l in range(len(a) - 2, 0, -1): # we need to begin at the second to last layer
                #Compute the updated error (i,e, deltas) for each node going from top layer to input layer

                deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
            deltas.reverse()
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0]+1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a