引例

活动选择问题

假设n个活动集合S，这些活动使用同一个资源。这个资源在某一时刻只能供一个活动使用，每个活动都有一个开始时间和一个结束时间。我们想选出时间不重叠的数量最多的活动集（假设活动按照结束时间单调递增排序）。

这个问题可以写出最优解的表达式但是求解的时候比较麻烦。

我们是否可以这样考虑，我们每次都挑选最早结束的活动，这样就算有活动比他早开始，但是因为比他晚结束，所以同样是一个活动还是早结束的活动更优。

代码比较简单，就不打了

原理

性质：我们通过局部最优解构造全局最优解。也就是我们可以考虑当前问题最优的选择，而不比考虑子问题的解。

如果一个问题最优解包含子问题最优解，称此问题有最优子结构性质。

每个小问题的解可由贪心选择获得，则称这个问题具有贪心选择性质。

k-优化算法

这里的k-优化是拿背包问题进行说明的，其他某些问题也可以使用。

大致过程：

首先按密度进行排序
1. 先拿取k件物品，如果重量大于背包重量c，则放弃这个选择（具体请看下面例子）
2. 对其余物品使用贪心算法
3. 进行$C_n^k$次上述过程找出贪心最优解

k-优化算法的优点是它将贪心算法与最优算法的偏差限定在$\frac{1}{k+1}$（如果没有这个限制可能会导致最优算法结果是100，而贪心算法结果是6的情况）

它的复杂度是 $n^{k+1}$。每次贪心选择要O(n)复杂度，一共进行$C_n^k$次

例：

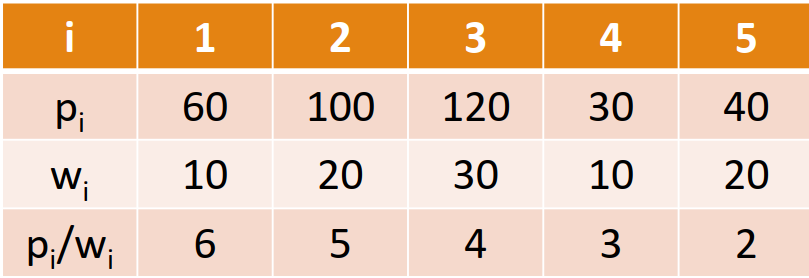
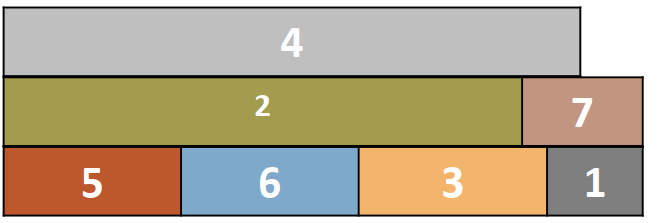
c=50, 如果使用2优化，我们可以

先取1、2，对其他物品再使用贪心，可以得到1、2、4，价值为190
先取1、3，可以得到1、3、4，价值为210
先取1、4，可以得到1、2、4
先取1、5，可以得到1、2、5，价值为200
先取2、3 …

多机调度问题

设有n个独立的作业{1, 2, …, n}, 由m台相同的机器进行加工处理。
作业i所需的处理时间为ti。现约定，每个作业均可在任何一台机
器上加工处理，但未完工前不允许终端处理。作业不能拆分成更
小的子作业。

求完成这些任务所需要的最短时间。

我们要想办法让分到m台机器上的时间尽可能平均，这样最后完成时间也会最短。因此我们可以按照时间排序，先把时间长的运行，之后再用时间短的进行填补

int machine[NR_MACHINE];
int get_min_time(int time[], int n, int machine_num)
{
	quick_sort(time, 0, n-1);
   if(machine_num >= n)
   {
       return time[0];
   }
   priority_queue <int,vector<int>,greater<int> > q;
   for(int i=0; i<machine_num; i++)
   {
       q.push(time[i]);
   }
   for(int i=machine_num; i<n; i++)
   {
       int temp = q.top();
       q.pop();
       q.push(temp+time[i]);
   }
}

prim,kruskal, dijkstra

这三个算法可以看这