搭配
本文最后更新于 2021年10月6日 晚上
含义
搭配是两个及两个以上的词组成的词汇表示。
例如:1
2
3strong tea vs. powerful tea vs. powerful drug
make a decision vs. take a decision
knock … door vs. hit … door
这些搭配有时候并没有什么语法规则,仅仅是约定俗称的习惯,因此单纯的基于规则进行进行词语匹配有时候无法找出这些搭配。
寻找搭配的方法
基于频率
基于频率的基本思想就是统计一个语料中二元组出现的次数。但是统计完成之后可能出现如下图所示情况。
of the in the等搭配毫无意义,因此我们需要想办法筛选出不需要的留下需要的。
一种方法是使用停用词表删去停用词,第二种方法是基于规则筛选掉某些不太可能出现搭配的方案,例如介词和副词搭配。
均值和方差
很多时候二元组并不是紧密相连的,他们之间往往有一定距离,并且还需要知道两个词的先后顺序。例如:1
2
3
4
5she knocked on his door
They knocked at the door
100 women knocked on Donaldson’s door
A man knocked on the metal front door
knock door搭配
这时我们可以从语料中获得平均偏移量(通过计算两个词之间的空格数).例如上面的四个词平均偏移量为(3 + 3 + 5 + 5) / 4 = 4
然后再计算平均偏移量的方差。
之后当我们寻找一个新的词时可以根据平均偏移量方差大小判断,如果方差过大我们可以认为他们不构成一个搭配(和这个词没有关系因此出现位置没有关联)
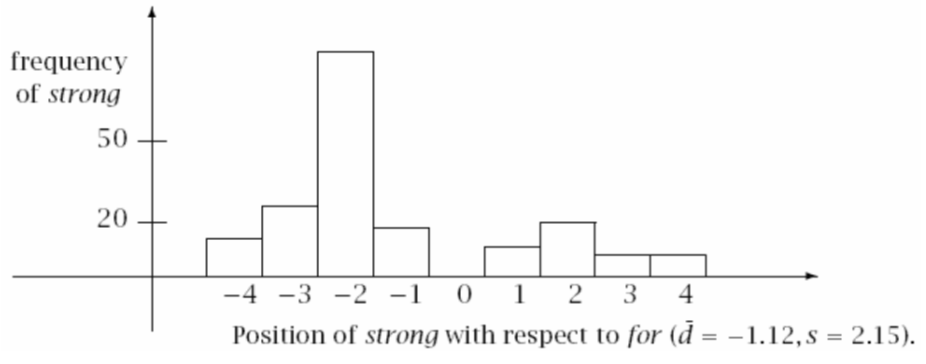
如图所示为strong距离for的位置,我们可以看到方差比较大,因此可以认为strong和for不是一个搭配。
如果均值接近于一,我们可以使用基于频率的方法发现搭配,如果均值远大于1,那么可以使用方差的方法寻找搭配
假设检验
有时候高频率和低方差是偶然出现的,例如new companies虽然经常出现,但是他们并不是搭配。
t检验
此时我们可以使用假设检验的方法。假设检验时评价一个事件是否是偶然事件。首先假设偶然事件为真,在这个事件为真的情况下计算发生的概率p,如果p大于某一个值我们就拒绝他。
对于寻找搭配问题。最关键的是如何定义高频出现的词语是偶然现象这个零假设。也就是说两个单词的出现时相互独立的,即p(w1, w2) = p(w1)p(w2)
我们可以把语料库看成N个二元组的序列,然后统计感兴趣二元组出现的次数(并且认为它是二项式分布)
 接收H0也就表示他们是无关的
接收H0也就表示他们是无关的
卡方分布
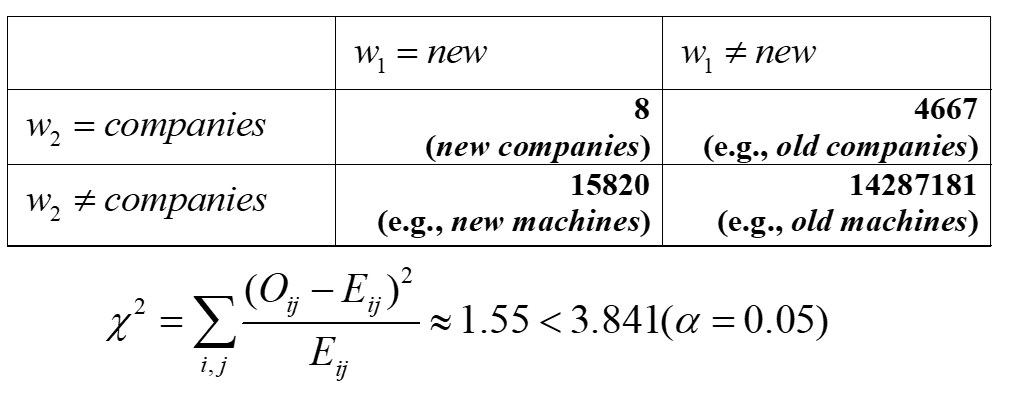
互信息
点互信息(在已知y的情况下获得x的信息量)
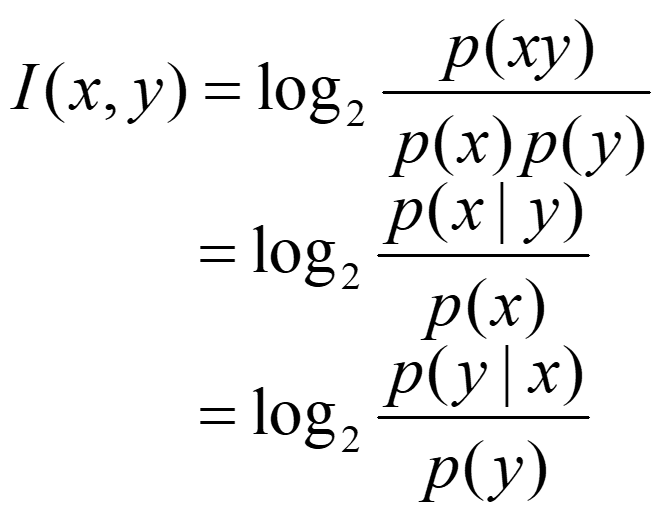
根据这个式子我们只需要求出y出现次数和x出现次数即总数目即可。
但是互信息高并不能说明依赖性就高,因为他还会受频率影响。但是它可以很好分辨出独立的情况,因为相互独立互信息为0.