引例

钢条切割问题

有一根长为$R_n$的钢条，切若干米获得的收益不同（例如切1米1元，切2米3元），请问怎样切割使得收益最大？

朴素的方法是我们可以把所有情况列举出来求最优解，但是总共有2^(n-1)种方案，复杂度显然过高，因此需要更简便的方法。

我们虽然是把它分成若干段，但是其实我们不是一瞬间把所有段都切好的，我们也是一条一条进行切割，所以问题可以转化为切一段和剩下所有段的最优解。即

其中$R_n$是长为n时的最优解。$P_i$是切长度为i可以获得的收益。

rod(int* p, int n)
{
    if(n == 0)
    {
        return 0;
    }
    int q = -2147483648;
    for(int i=1; i<=n; i++)
    {
        q = max(q, p[i]+rod(p, n-i));
    }
    return q;
}

这是上面说明的递归算法。事实上，这种方法复杂度仍然很高，还是指数级复杂度。我们可以输入4模拟一下过程。

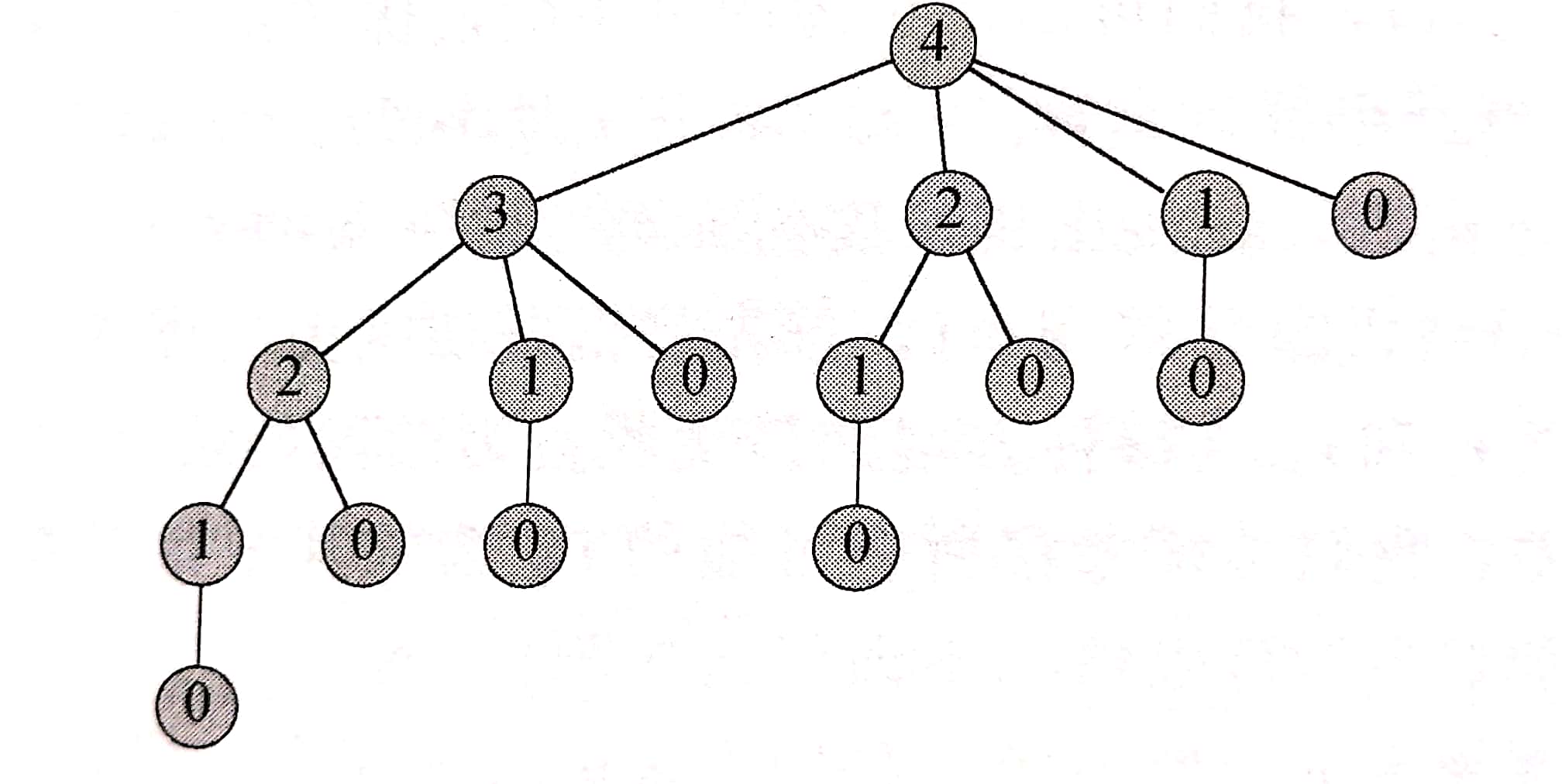
从图中我们可以看出，求解n=0求了7次，求解n=1求了4次。速度慢的原因可能就是我们重复求解相同的问题。

用动态规划的方法求解问题

因为我们总是求解相同的问题，那么是否可以在第一次求解这个问题的时候把结果记录下来呢？那么之后再需要这个结果的时候就可以直接去取了。

用这种思路求解问题有两种方法：

• 带备忘的自顶向下法。这种方法仍然是按普通的方法求解。但是用了一个数组或散列表记录了每个子问题的解，这样每次求解时先从表中查询，没有再求解。
• 自底向上法。这种方法要求我们正确的划分问题，使得每个子问题都是由更小的子问题得来的，这样我们只需要从最小的子问题求起就可以解决。

自顶向下
rod(int* p, int n)
{
    int r[n+1];
    for(int i=0; i<=n; i++)
    {
        r[i] = -2147483648;
    }
    return memo_aux(p, n, r);
}

memo_aux(int* p, int n, int* r)
{
    int q;
    if(r[n] >= 0)
    {
        return r[n];
    }
    if(n == 0)
    {
        q = 0;
    }
    else
    {
        q = -2147483648;
        for(int i=1; i<=n; i++)
        {
            q = max(q, p[i]+memo_aux(p,, n-i, r));
        }
    }
    r[n] = q;//把算出来的值存进去
    return q;
}

自底向上

rod(int* p, int n)
{
    int r[n+1];
    r[0] = 0;
    for(int i=1; i<=n; i++)
    {
        int q = -2147483648;
        for(int k=1; k<=i; k++)
        {
            q = max(q, p[k] + r[j-k]);
        }
        r[i] = q;
    }
    return r[n];
}

上面求解的都是最大收益，但是没有说明到底如何切割。从自底向上的方法中我们可以看出，对于每次最大都是p[k]+r[j-k]和q
进行比较。也就是对于每个问题我们最多只会切一刀，所以我们只需要记录切的那一刀

子问题图

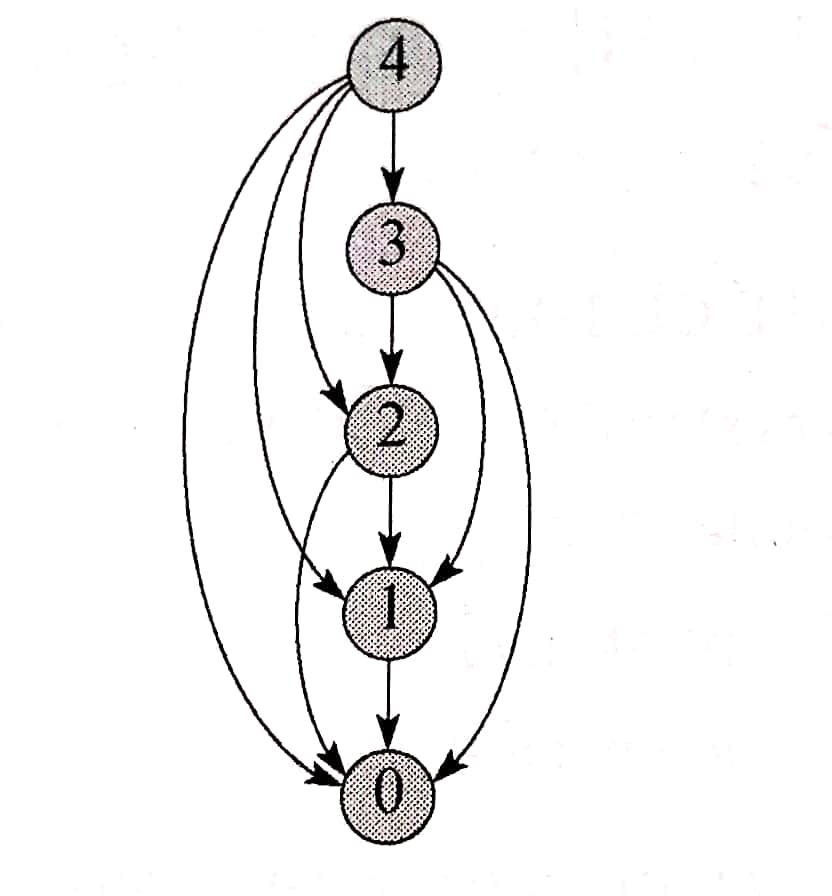
上图是这个问题的子问题图。图中的线表示某个子问题求解需要用到那些子问题。从图中我们很容易看出我们可以先求解问题0，然后求解问题1，直到求解所有子问题。

背包问题

背包问题

动态规划原理

最优子结构

如果一个问题最优解包含子问题的最优解，那么就称这个问题有最优子结构性质。因此想要知道一个问题能否用动态规划，这个问题是否有最优子结构是一个线索。

此外，两个子问题应该具有无关性，即一个子问题的解不影响另外一个问题。

例如，找无权最长路径时（该路径必须是简单路径，没有环），我们可以把问题分解成从a到b最长路径再从b到c最长路径。但是conga到b最长路径对后面一个求解是有影响的，因为不能形成环所以有些路就不能走。

说明最优子结构性质一般采用反证法，即假设一个子结构不是最优的，那么一定还有比他更优的，那么把这条更优的替换上去才是最优。

例如找最短路径问题，如果某一子路径的两个端点之间有更短的路径，那么把这条更短的路径替换上去才是最优。

重叠子问题

重叠子问题就是我们应该反复求解规模不同但求解方式相同的子问题。

重构最优解

通常把每个子问题所做的选择存在一个表中，这样就不必根据收益重构这些信息。

例如上面求解如何切割就是重构最优解，这样可以减少我们求特定问题的时间。

备忘

备忘是自顶向下时使用的策略。它的思路就是将求解过的存到一个表中，要的时候再用。

最长公共子序列

如果一个子序列即是X的子序列，又是Y的子序列，那么可以把这个序列称作公共子序列。现在任务是查找最长公共子序列。子序列只需要下标单调递增就可以，不一定要连续。

如果x的长度是m，y的长度是n。那么Xm = Yn就说明最长子序列中一定包括Xm，之后只需要在Xm-1和Yn-1中寻找。

如果Xm != Yn，那么最长子序列要么在Xm-1和Y中找要么在X和Yn-1中找。

根据上面的陈述，我们可以得到一个递推式。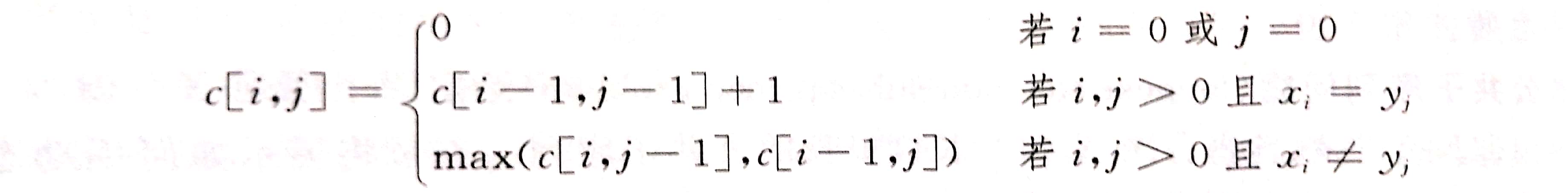

int* length(int* x, int* y)
{
    int m = x.len;
    int n = y.len;
    int c[m+1][n+1];
    for(int i=1; i<=m; i++)
    {
        c[i][0] = 0;
    }
    for(int i=0; i<=n; i++)
    {
        c[0][i] = 0;
    }
    for(int i=1; i<=m; i++)
    {
        for(int k=1; k<=n; k++)
        {
            if(x[i] == y[k])
            {
                c[i][k] = c[i-1][k-1] + 1;
            }
            else if(c[i-1][j] >= c[i][j-1])
            {
                c[i][k] = c[i-1][k];
            }
            else
            {
                c[i][k] = c[i][k-1];
            }
        }
    }
    return c;
}

旅行商问题

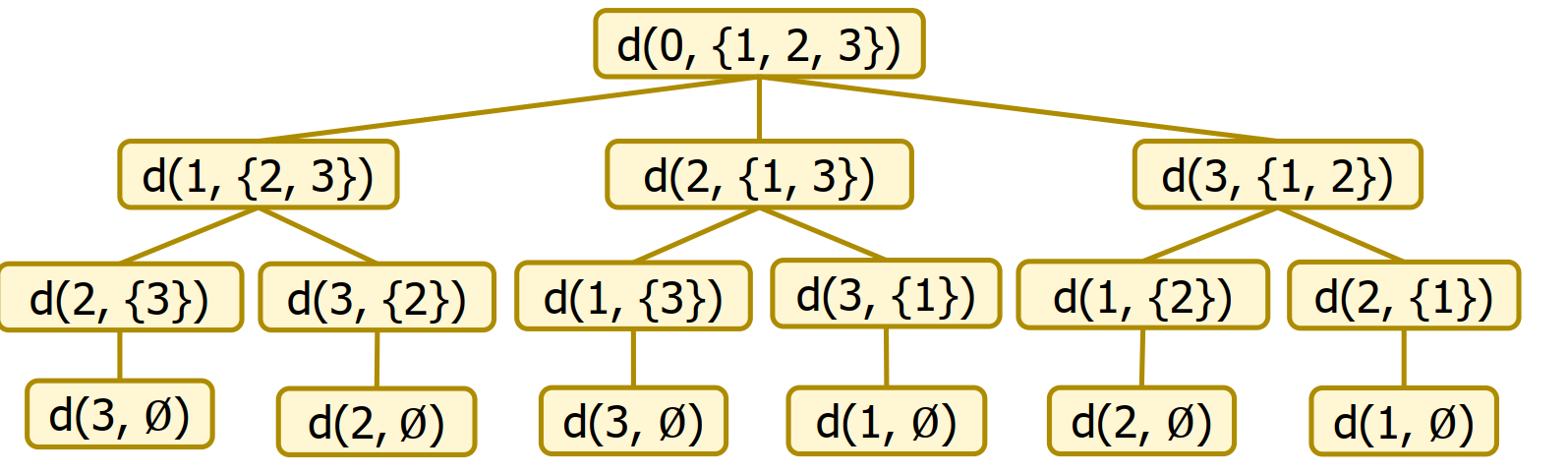
旅行商问题是给定一系列城市和每对城市之间的距离, 求访问每一座城市一次并回到起始城市的最短回路。

• 设 s, s1, ⋯, sp, s 是从 s 出发的一条路径长度最短的简单回路。
• 假设从 s 到下一个城市 s1的最短路径已经求出，则问题转化为求从 s1到 s 的最短路径。
• 显然s1到s的最短路径就是s1, …, sp, s.因为前面说了s, s1, …, sp, s是最短路径

由此我们可以得到递推公式

其中$\delta(i, S)$表示从i出发回到原点的最短路程。

这是状态空间树。例如我们想从3经过1、2回到原点。那么最短路径是

{
    for (i=1; i<n; i++) d[i][0]=w[i][0];
    for (j=1; j<2n-1-1; j++)
    for (i=1; i<n; i++)
    {
        if (I ∉ Si)
        {
            for each k∈S
            i, d[i][Si]=min{c[i][k]+d[k][{Si-k}]|k∈Si};
        }
    }
    for each k∈V[2n-1-1], d[0][2n-1-1]= min{c[0][k]+d[k][2n-1-2]};
    return: d[0][2n-1-1];
}