无后效性

无后效性是一个问题可以用动态规划求解的标志之一，理解无后效性对求解动态规划类题目非常重要

概念：某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响（某度上找的定义）

理解：无后效性指的是之前做过的事现在还可以继续去做，这便是前一阶段做的事对后一阶段无影响。如果前面做过了后面便不能去做或者做的事受限这便是有后效性

例：这篇博客讲的很清楚

01背包问题

动态规划更多可看

问题描述：

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

我们可以用一个数组dp[i][c]来表示考虑前i个物品并且剩余容量为c时的最大价值。

首先要说明它满足最优子结构性质:

  1. 假设最优解为($x_1, x_2$, …).$x_i$可以选取0或1.
  2. 现在随机选取最优解中的部分($x_1, x_2,…x_i$)。假设它不是子问题的最优解，那么一定存在一个比他更优的解($y_1, y_2,…y_i$)。使得value($x_1, x_2,…x_i$)<value($y_1, y_2,…y_i$)
  3. 则value($y1, y_2, …y_i, x{i+1}…x_n$)>value($x_1, x_2,…x_n$)。与假设矛盾
  4. 因此($x_1, x_2, … x_i$)一定是子问题的最优解

我们只考虑第i件和第i-1件，如果第i件没有装，那么dp[i][j] = dp[i-1][j].如果第i件装了，那么剩余容量就会减小并且加上第i件物品的价值为dp[i][j] = dp[i-1][j-goods[i].w] + goods[i].v;

递推关系式为

struct Good{
    int w;
    int v;
}goods[101];
int dp[101][1001];
int n,S;//n表示有n个物品，S表示背包的最大容积
for (int i = 1; i <= n; i++)
{
    for (int j = goods[i].w; j <= S; j++)
        dp[i][j] = max(dp[i-1][j], dp[i-1][j - goods[i].w] + goods[i].v);
}

实际上这里的二维数组可以优化变为一维数组

dp[i][j] = max{dp[i-1][j-w[i]]+v[i]，dp[i-1][j]，这里的i与i-1实际上是第i个物体与第i-1个物体，而这个可以用数组下标直接代替，这样便可以用一维数组解决背包问题，但是一维数组与二维数组的区别是二维数组保存了前i个物品所可以获得的最大价值，而一维数组只能保存题目要求的s个物品的最大价值，因此用一维还是用二维因题目而异

dp[j] = max{dp[j]，dp[j-w[i]]+v[i]}。从这个方程中我们可以发现，有两个dp[j]，但是要区分开。等号左边的dp[j]是当前i的状态，右边中括号内的dp[j]是第i-1状态下的值。

所以为了保证状态的正确转移，我们需要先更新等号左边中的dp[j]（当前状态的dp[j]）。

代码：

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n,maxv;
    cin>>n>>maxv;
    int w[1001],v[1001];
    int dp[1001];
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i];
    }
    for(int i=0;i<=maxv;i++)
    {
        dp[i]=0;
    }
    for(int i=1;i<=n;i++)
    {
        for(int k=maxv;k>=w[i];k--)/*这里是因为当背包体积小于物品体积时不可能成立，相当于if(k<w[i]){dp[i][k]=dp[i-1][k];}*/
        {
            dp[k]=max(dp[k],dp[k-w[i]]+v[i]);
        }
    }
    cout<<dp[maxv]<<endl;
    return 0;
}

在这段代码中，k之所以要从maxv出发，是因为现在我们更新的dp[k]可能会对之后的求解造成影响。

例如：

  • 当i=1时，这个物品重量是2，价值是3，也就是dp[2] = 3
  • 然后求到dp[4]时，dp[4] = dp[4-2]+3 > dp[4].所以现在dp[4] = 6.但是实际上应该是3，这就是前面更新的dp[2]影响到了后面求解，破坏了无后效性。
  • 最开始那个之所以可以从前往后求解是因为它是根据dp[i-1]进行转移的，dp[i-1]的值已经确定了，这时我们更新就不会影响求解。

拓展问题

继续0-1背包问题，如果在上面的问题加上一个限制条件，所选择的物品必须恰好装满背包，否则输出-1。这时数组初始化为负无穷

#include <iostream>
using namespace std;

#define MAXSIZE 100
int w[MAXSIZE];
int v[MAXSIZE];
int maxv;
int n;
int dp[MAXSIZE][MAXSIZE];

int max(int a, int b)
{
    if (a > b)
        return a;
    else
        return b;
}

int main()
{
    cin >> n >> maxv;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i] >> v[i];
    }
    //初始化，当容积为0时，即不能装入，最大价值即为0
    for (int i = 1; i <= n; i++)
    {
        dp[i][0] = 0;
    }

    //初始化为-1，表示没有装满
    for (int i = 0; i <= n; i++)
    for (int j = 1; j <= maxv; j++)
        dp[i][j] = -1;

    for (int i = 1; i <= n; i++)
    {
        for (int j = maxv; j >= w[i]; j--)
        {
            //dp[i - 1][j - w[i]] != -1表示容积为j - w[i]时没有装满，所以当容积为j，装w[i]时一定不能装满
            //dp[i - 1][j - w[i]] + v[i] > dp[i-1][j]表示装入物品i时签好装满并且总价值比前i-1个物品的总价值要大
            if (dp[i - 1][j - w[i]] != -1 && dp[i - 1][j - w[i]] + v[i] >= dp[i - 1][j])
                dp[i][j] = dp[i - 1][j - w[i]] + v[i];

        }
        for (int j = w[i] - 1; j >= 1; j--)
            dp[i][j] = dp[i - 1][j];
    }

    cout << dp[n][maxv] << endl;

    return 0;
}

其它大致相同，现在dp[i][j]表示的是恰好装j空间时价值的最大值

元组法：

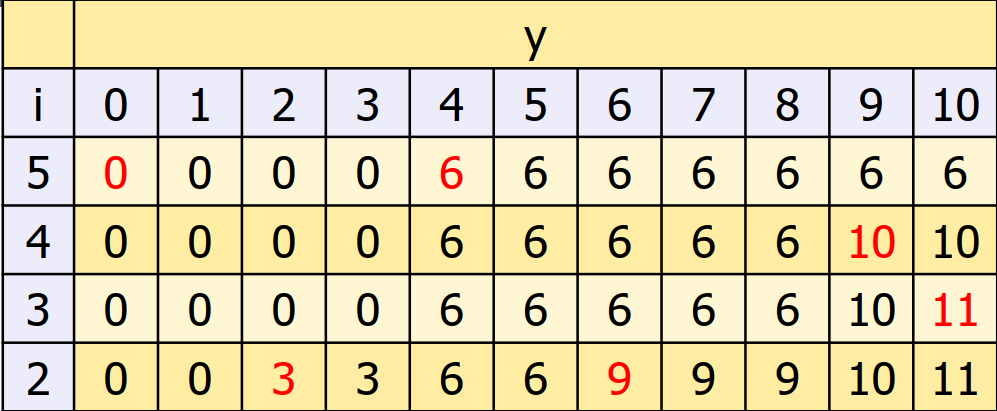
这是动态规划数组，可以看到里面存了大量重复的值，我们可以只记录变化的值（图中红色部分）从而减小空间消耗。


首先i=4时是在i=5基础上变化的。i=4时w=5,v=4,所以跳点可能是(0, 0) (5,4) (4, 6) (9, 10). 因为(5, 4)比(4, 6)重量大价值低所以无论后面怎么增加一定没有(4, 6)好，因此可以把(5, 4)省略

完全背包

题目：有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

for (i = 1; i <= n; i++)
{
    for (j = goods[i].w; j <= S; j++)
        dp[j] = max(dp[j], dp[j - goods[i].w] + goods[i].v);
}//不是很理解，但是先把模板记下吧

这个代码和01背包代码十分相似，只有循环方向不同，为什么可以这样做呢？因为01背包要求每个物品只能选一次，因此根据这个式子，有可能会导致多选的就是dp[j - goods[i].w],如果从前往后循环，j-goods[i].w可能是已经选择了当前物品的情况

可以去看

多重背包

有N种物品和一个容量为V的背包。第 i 种物品最多有n[i]件可用，每件费用是c[i]，价值是w[i]。求将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

实际上可以转化为01背包，把每一种物品中多件拆开

int k = n + 1;
	for (int i = 1; i <= n; i++) {
		while (number[i]>1) {
			w[k] = w[i];
			value[k] =value[i];
			k++;
			number[i]--;
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = v; j >= w[i]; j--) {
			f[j] = max(f[j], f[j - w[i]] + value[i]);
		}
	}

但是这样可能导致时间复杂度过高，可以考虑采用二进制思想，每一个数例如7可以用二进制来表示，而这样我们就可以把它拆为3个数，7二进制为111，所以可以拆为100,010,001，这样我们就只需要储存3个数，降低了时间复杂度。但是假如不是正好的话
例如13 ，二进制为1101，则可以分解为0110,0001,0010,0100（如果最好不足2^i，则取x-2^i-1)

int num[maxn][2], dp[maxn];
int N, V, c, w, n, tot;
memset(dp, 0, sizeof dp);
cin >> V >> N; tot = 1;
for(int i = 1; i <= N; ++i)
{
	cin >> c >> w >> n;
	for(int k = 1; k < n; k<<=1)//左移求下一个所需二进制数 
	{
		num[tot][0] = k*c;
		num[tot++][1] = k*w;//注意这时我们把若干物体看为1个物体，它的总重量也要变
		n -= k;
	}
	num[tot][0] = n*c;
	num[tot++][1] = n*w;
}
for(int i = 1; i < tot; ++i)
{
	for(int j = V; j >= num[i][0]; --j)
		dp[j] = max(dp[j], dp[j-num[i][0]]+num[i][1]);
}