基础

例：

假定文法为：
(1) S->aAcBe
(2) A->b
(3) A->Ab
(4) B->d

将abbcde归约到S

栈     动作
a	   进a
ab	  进ab
aA	  A->b
aAb	 进b
aA      A->Ab
aAc     进c
aAcd    进d
aAcB	B->d
aAcBe	进e
S	S->aAcBe

该过程和自顶向下正好相反，它从规则右端寻找是否有匹配规则，然后将他归约成左端，最后得到起始字符为匹配完成。

因为右端可能会有多条相同规则，因此问题的关键是使用哪一个产生式进行归约。

名词定义：

  1. 短语： 文法G[S], $\alpha \beta \delta$是文法G的一个句型 且$S \overset{*}{=}> \alpha \beta \delta \, 且 \, A \overset{+}{=}> \beta$.则称$\beta$是A的短语
  2. 直接短语： 若有A=>$\beta$则称为直接短语
  3. 句柄： 一个句型的最左直接短语称为句柄

例如文法：

E->T | E+T
T->F|T*F
F->(E)|a
找出$a_1 * a_2 + a_3$的短语，直接短语和句柄

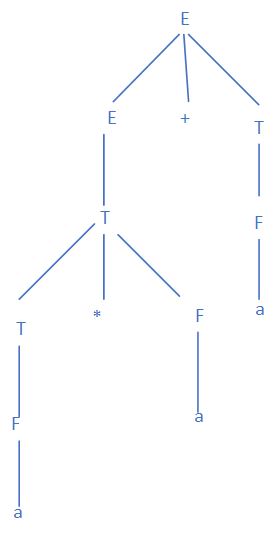
$a_1 , a_2 , a_3 , a_1 a_2 , a_1 a_2 + a_3$是$a_1 * a_2 + a_3$的短语

$a_1 , a_2 , a_3$是直接短语

$a_1$是最左直接短语

$a_2 + a_3$不是短语，因为$a_2 + a_3$只能由E->E+T开始，但是这条规则推到结果后没有$a_2 + a_3$的叶子节点

短语都是一颗生成树中子树的叶子节点从左向右排列。句柄是最左边的只有父子两代节点的所有叶子自左向右排列。

规范归约定义

如果一序列是规范归约，令序列$a_n, a_1, \dots, a_0$为一个规范归约那么他要满足：

  1. $a_n = a$
  2. $a_0 = S$
  3. 对于任何i, $a_{i-1}$是$a_i$将句柄替换成相应产生式的左部符号得到的

算符优先分析法

优先级定义：

  • a <$\cdot$ b: b的优先级高
  • a = b
  • a>$\cdot$ b

算符文法定义：设有一个文法G，如果G中没有形如A->BC的产生式，其中B和C都是非终结符，则称G为算符文法

算符优先文法定义： 设文法G是一个不含任何$\varepsilon$的算符文法，且对于任何一个a，b来说

  • a = b: 文法中有形如A->ab, A->a$\beta$b的产生式，即在语法树中是平级的
  • a <$\cdot$ b: A->aB且B$\overset{+}{=}$>b或B$\overset{+}{=}>$ Cb。即a小于B子树中的最左边节点
  • a >$\cdot$ b: A->Bb且B$\overset{+}{=}$>b或B$\overset{+}{=}>$ aC

之所以Cb也可以是因为不能同时出现两个非终结符，因此C开头的话前面没有终结符，此时b还是子树下的第一个终结符

FIRSTVT, LASTVT

FIRSTVT ( P ) = {a | $P\overset{+}{=}> a \dots 或 P \overset{+}{=}> Qa \dots, a \in V_T , P, Q \in V_N }$

LASTVT( P ) = {a | $P\overset{+}{=}>\dots a 或 P \overset{+}{=}> \dots aQ , a \in V_T , P, Q \in V_N }$

如果有A->aB的产生式，则a < FIRSTVT(B)。如果有A->Ba的产生式，则a > LASTVT(B)

构造FIRSTVT( P )的方法：

  • 若有产生式P->a或者P->Qa， 则$a \in FIRSTVT( P )$
  • 若a$\in FIRSTVT( Q )$， 且有产生式P->Q, 则a$\in FIRSTVT( p )$

实现思路：

  • 可以使用一个数组F[X, a]，如果F[X, a]为真，表示a$\in FIRSTVT( X )$
  • 首先按照规则1将数组赋初值，并且用一个栈将所有为真的(X, a)放入栈中，进行如下运算
    • 如果stack不空，则弹出栈顶，记为(Q, a). 对于所有P->Q的产生式，若F[P, a]为假，则将其置为真并且将他放入栈中
      • 重复上述过程，直到栈为空

算符优先分析方法

一些基本定义：

  • 素短语： 它是一个短语，并且它至少有一个终结符， 并且除了他之外不包含更小的素短语。可以首先看成有终结符的短语，然后在这些候选项中排除
  • 最左素短语： 处于句型左边的素短语。且算符归约方法中的可归约串是最左素短语

例如: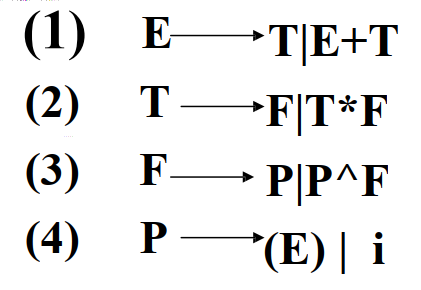
考虑句型P * P + i的最左素短语

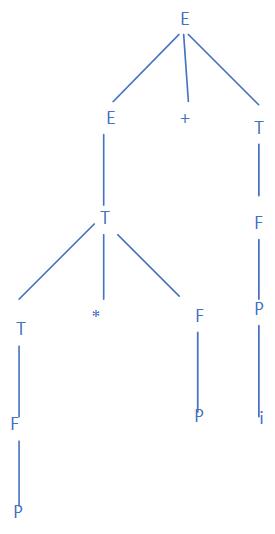
短语为P P + i, P P, P, i

素短语为P * P 和 i

最左素短语为P * P

一个算符优先文法的句型为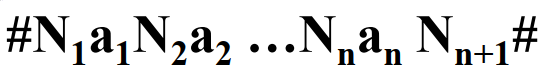

因为算符文法的要求是不能出现两个相邻的非终结符，因此图中两个非终结符中间必须有终结符插入。

一个算符优先文法G的任何句型的最左素短语满足下列条件的最左子串

  • $a_{j-1} < a_j$
  • $aj = a{j+1}, \dots , a_{j-1} = a_j$
  • $ai > a{i+1}$

也就是说左右两边优先级都比他低，因此他会被最先归约

使用算符优先文法发现最左素短语的过程

  1. <标记最左素短语的左端，=出现在最左素短语的内部，>出现在最左素短语的右端
  2. 从左端开始扫描串，直到遇到第一个>(最右端符号)为止
  3. 向左扫描栈（弹出栈顶）， 跳过所有的=， 直到遇到第一个<为止
  4. 我们弹出的符号是最左素短语

算符优先归约就是不断寻找最左素短语并将其归约的过程

例如：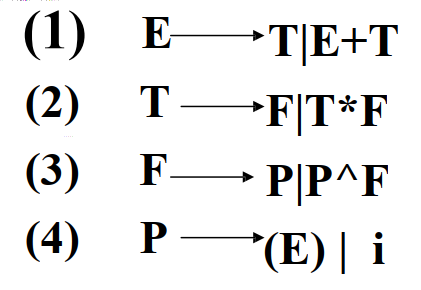

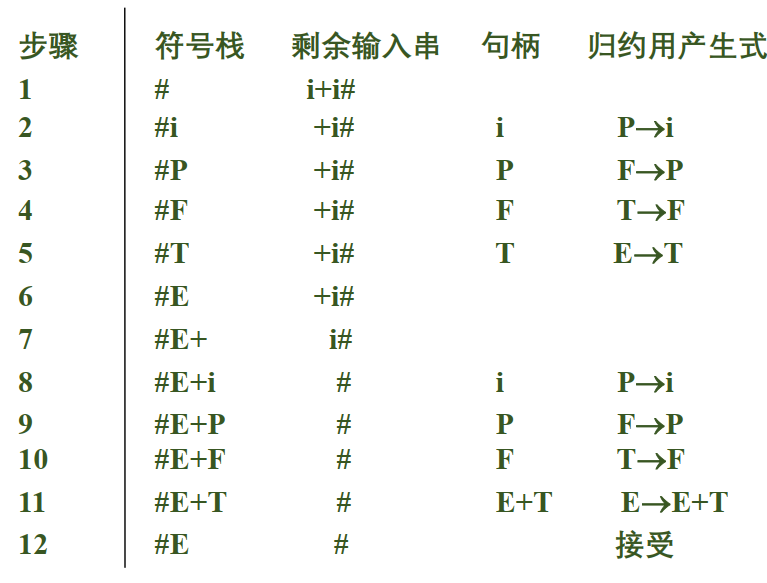
优先函数

在实际分析中，用两个优先函数f, g, 把终结符Q和两个自然数f(Q)和g(Q)对应，使得：

  • 若Q1 < Q2， 则f(Q1) < g(Q2)
  • 若Q1 = Q2, 则f(Q1) = g(Q2)
  • 若Q1 > Q2, 则f(Q1) > g(Q2)

称f为入栈优先函数，g为比较优先函数

还是上面的例子，优先函数得到的关系表为

但是优先函数中的空白项都是模糊的，不利于错误处理，它的优点是所需空间比较小

构造方法：

  • 为每个终结符创建f和g，总共2n个节点
  • 如果a > b或a = b, 则画一条$f_a$到$g_a$的弧(使用邻接矩阵)
  • 如果a < b或a = b,则画一条$g_a$到$f_a$的弧
  • 如果构造的图中有环路,则不存在优先函数，如果没有环路，则将f(a)设为$f_a$出发所能到达的个数，g(a)设为从$g_a$到达的节点个数

优缺点

由于没有定义非终结符之间的优先关系，所以无法归约单个终结符组成的可归约串(一个字符的字符串）

LR分析法

LR分析的基本思想是，在规范归约(最右推导) 的过程中，一方面记住已有的历史，一方面根据产生式判断未来可能有的符号。

基本结构：

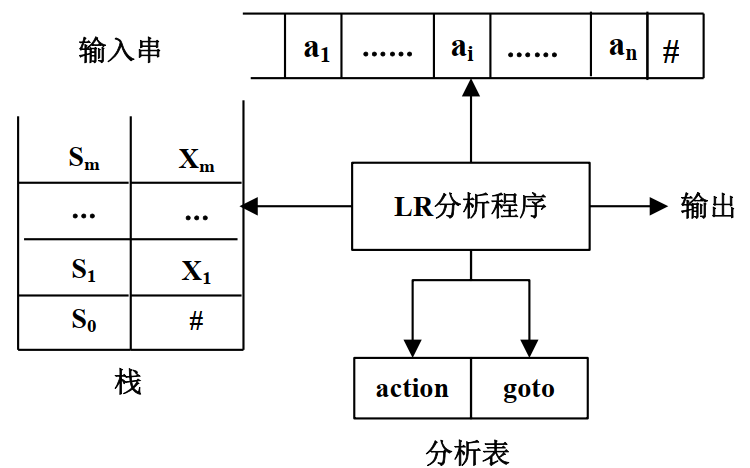
上面的$a_i$是输入串，左边是一个符号栈，里面存放了非终结符。分析器会把栈顶符号和当前输入符号为输入，送给两个分析表，得出下一步状态。它实际上是一个下推自动机

LR文法定义：如果我们可以为文法构造一个分析表，使得分析表每个入口都是唯一的，那么这个文法式LR文法。如果我们每次可以向前检查k个符号，那么它是LR(k)文法

分析表构造

概念：

  • 前缀： 前缀是该字的任意首部。如abc的前缀可以是$\varepsilon$, a, ab, abc
  • 活前缀： 是规范句型(最右推导过程中的一个句型) 的一个前缀。之所以称为活前缀，是因为添加一些符号之后，可以使他成为最右推导
    LR分析工作的任何时候，栈里的文法符号应该构成活前缀

  • 项目： 对于一个文法G，我们需要构建一个NFA识别活前缀，这个NFA的每一个状态是一个项目
    例如A->XYZ,他有四个项目

    A->*XYZ
    A->X*YZ
    A->XY*Z
    A->XYZ*

    产生式A->$\varepsilon$只对应一个产生式A->*

    项目的含义是我们已经看到的部分和我们希望看到的部分。例如A->X*YZ表示我们已经看到了X得到的字符串，我们还希望看到YZ得到的字符串

活前缀识别NFA构造

  • 如果项目i和j来自同一个产生式，且j的圆点只落后i一个位置,那么从状态画一条弧从状态i到状态j，并且跳转条件为$X_i$
    如:
  • 如果i圆点后的符号为非终结符，如$X->\alpha \cdot A \beta$，那么就从状态i画$\varepsilon$到所有$A->\cdot \gamma$状态
  • 凡是圆点在最右端的项目称为归约项目。S->$\alpha*$称为接受项目

根据上面的规则就可以构造NFA，例如：

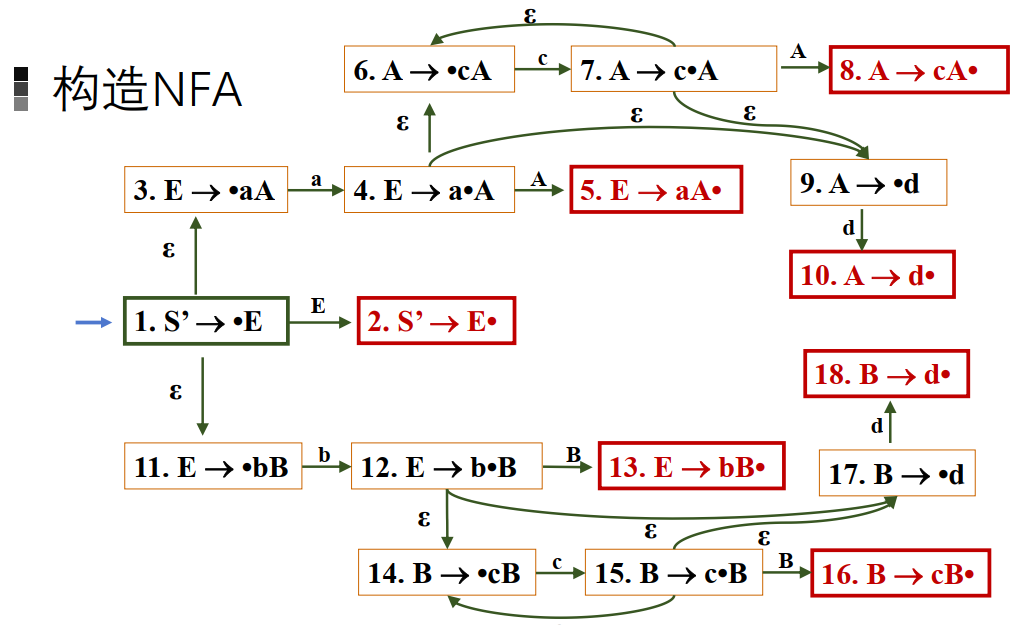
然后进行确定化和最小化

项目集规范族构建

我们可以通过项目集规范族来构造分析表。构造方法为：

  • 假设G是以S为开始符号的文法，构建一个$S^{\prime}$包含G中所有文法并且增加了$S^{\prime}->S$,以$S^{\prime}$作为$G^{\prime}$的开始符号。这样，只会有一个$S^{\prime}->S\cdot$的接受状态
  • 构建CLOSURE(I):
    • I中的项目都属于CLOSURE(I)
    • 若A->$\alpha \cdots B \beta \in CLOSURE(I)$,则B的任何产生式$B->\cdots \gamma$也属于CLOSURE(I)
    • 重复上面两步直到CLOSURE(I)不再增大
  • 构建GO(I, x): GO(I, x) = CLOSURE(J) J={任何形如$A->\alpha X \cdot \beta$的项目 | $A->\alpha \cdot X \beta \in I$}

自底向上语法分析10

分析表构建

构建过程：

  1. 令包含$S^{\prime}->S$的集合$I_k$为分析器的初态
  2. 若项目$A->\alpha \cdots a \beta \in I_k$且$Go(I_k , a) = I_j$,则ACTION[k, a]的动作为将(j, a)移进栈，简记为$S_j$
  3. 若项目$A->\alpha \cdots \in I_k$，对于任何终结符a(包括#),置ACTION[k, a]为使用产生式A->$\alpha$进行归约，记为$r_j$(假定A->$\alpha$是第j个产生式
  4. 若项目$S^{\prime}->S \cdots \in I_k$,则ACTION[k, #]为接受
  5. 若GO($I_k$, A) = $I_j$,A为非终结符，则GOTO[k, A] = j
  6. 分析表中的空余位置填上报错标志


例2:

冲突

  • 移进-归约冲突： 对于当前字符，如果一条规则要求移进，而另一条规则进行归约，则会产生冲突。例如
    L0
    A->$\alpha B \cdot \beta$
    B->$\alpha B \cdot$
  • 归约-归约冲突： 有两条规则对同一前缀进行归约
    L0
    A->$\alpha B \cdot$
    B->$\alpha B \cdot$

    SLR语法

SLR主要解决归约-归约冲突，它通过归约时参考FOLLOW集解决。现在归约时只对FOLLOW集中的终结符进行归约，其他报错。

例如同时有n个归约项目$B_1 -> \alpha \cdot , B_2 -> \alpha \cdot , B_3 -> \alpha \cdot …$。如果FOLLOW($B_1$),FOLLOW($B_2$), FOLLOW($B_3$)不相交，则采用如下方法解决

  • 如果a$\in FOLLOW(B_i )$,则使用产生式$B_i -> \alpha \cdot$进行归约
  • 否则报错

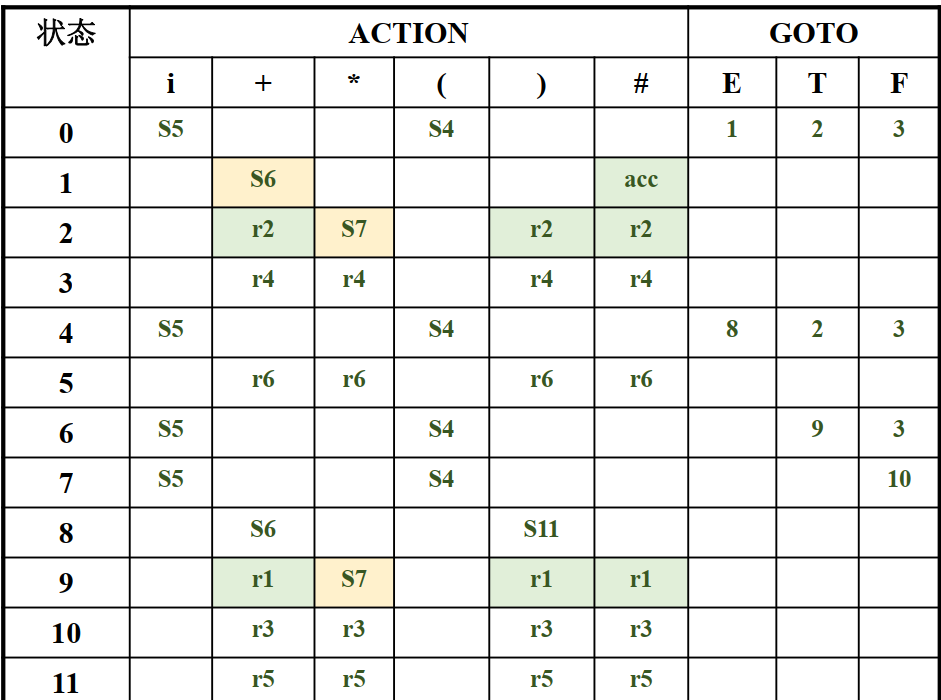
并且$I_1: S^{\prime} -> E \cdot \quad E->E \cdot + T$.其中S^{\prime}的FOLLOW集为{$}。因此$I_1$中只有#会进行归约

LR(1)文法

LR(1)文法对项目求法进行了扩充，现在项目是一个二元组[$A->\alpha \cdot \beta , a_1 a_2 \cdots a_k$]，其中前面一项和原来相同，后面一项是向前搜索串（展望串）。每次进行归约时只对展望串中的字符进行归约

构造闭包CLOSURE(I)的方法：

  1. I中的任何项目属于CLOSURE(I)
  2. 若[$A->\alpha \cdot B \beta , a$]属于CLOSURE(I), B->$\gamma$是一个产生式，那么对于FIRST($\beta a$)中的每个终结符b，将[$B-> \cdot \gamma , b$]加入CLOSURE(I)
  3. 重复上面两步直到不再变大

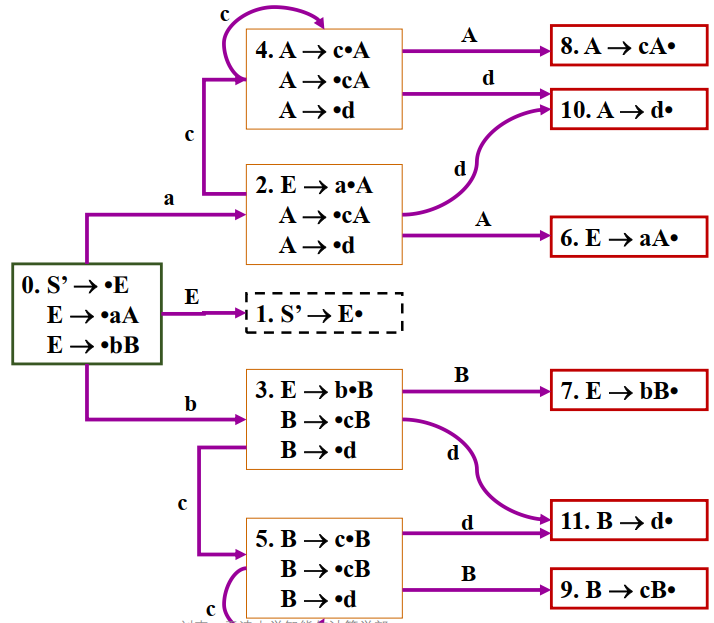
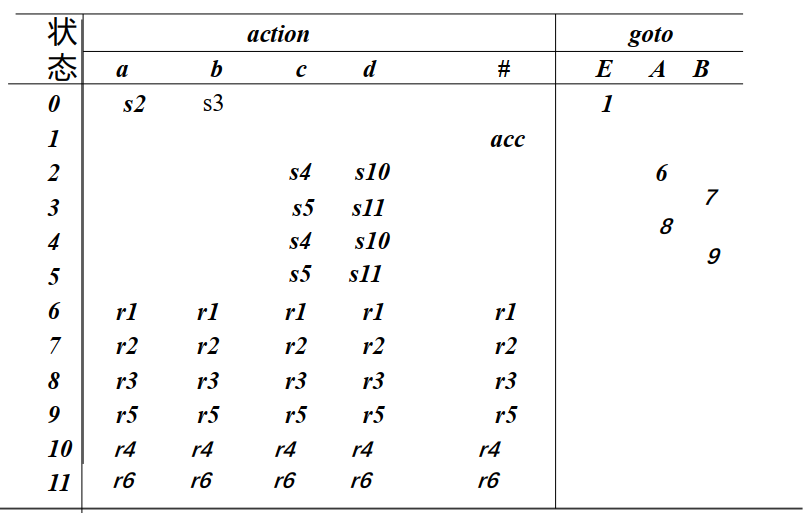
例如：

根据S->$\cdot CC, #$， FIRST(C#) = {c, d}, 因此C->$\cdot cC, c|d \quad C->\cdot d, c|d$

分析表使用

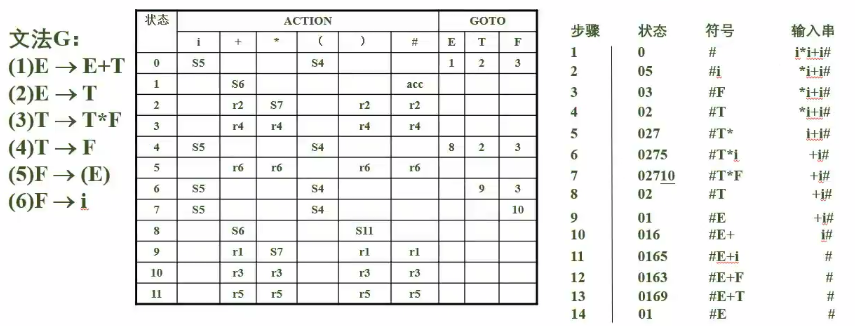
动作：

  • si: 将当前输入符号放入符号栈并进行跳转到i状态
  • rj: 使用第j个产生式($A->\beta$)进行归约，弹出|$\beta$|个符号和栈顶状态，压入A并查询现在栈顶状态的GOTO表进行跳转

例如上图第二个状态使用第六个产生式进行归约，弹出一个符号和5状态，压入F。此时栈顶符号是0，栈顶状态是F，查0状态的GOTO表得跳转到2状态

此外符号栈弹出几个符号，状态栈就要相应的弹出几个状态。例如第7步中弹出了三个符号，然后也要弹出3个状态 此时状态栈中只有0，然后再查0的GOTO表