字符串匹配是在一个长度为s的t串中找到和长度为m的p串相同的部分。t串是匹配串，p串是模式串

Pabin-Karp算法

它的基本思想是哈希。即将匹配串中每一个长度为m的子串进行哈希并与p串的哈希值进行比较。

假设模式串p[1…m]，得到哈希值的算法为

p = （p[m] + 10(p[m-1] + 10(p[m-2] + … + 10(p[2] + 10(p[1]))…)） % q — 霍纳法则

q是为了防止超范围的，10是基数，可以变成其他值

对于t串（匹配串），它的处理方法与p串相同，但是还需要进行移动，移动的方法为

$t_2 = 10(t_1 - 10^{m-1}T[s+1]) + T[s+m+1]$

其中T[s+m+1]是原来字符串的高一位，T[s+1]就是原来字符串的最低位。也就是减去最低位然后将字符串左移一位再加上最高位。

$10^{m-1}$可以使用快速幂的方法在O(lgm)时间计算完。

在计算完所有子串之后就可以对每一个哈希值进行比较了。如果p串哈希值和子串哈希值相同并不能说明二者一定相同，还可能产生哈希冲突。因此还需要对每一个字符进行匹配。

bool match(string T, string P, int d, int p)
{
    int n = T.size();
    int p = P.size();
    int h = d^m-1 mod q;
    int p = 0;
    int t = 0;
    for(int i=0; i<m; i++)
    {
        p = (d * p + P[i] ) % q;
        t = (d * t + T[i] ) % q;
    }
    for(int i=0; i<n-m; i++)
    {
        if(p == t)
        {
            int k;
            for(k=0; k<m; k++)
            {
                if(P[k] != T[i+k])
                {
                    break;
                }
            }
            if(k == m)
            {
                return true;
            }
        }
        t = (d * (t - T[s+1] * h) + T[s+m+1]) % q;
    }
    return false;
}

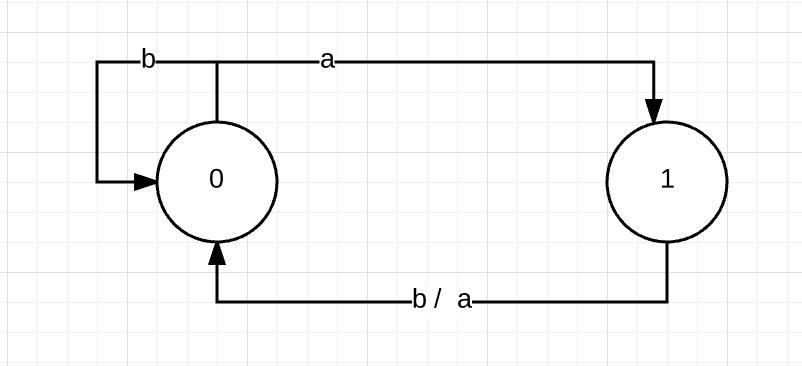
有限状态自动机法

例如：

首先0和1就是两个状态，而输入就是a和b。根据输入可以在0和1之间转移。

例如：输入为ababa，初始状态是0.那么首先输入a转移到1，输入b转移到0，输入a又转移到1依次进行下去。

而字符串匹配也可以用类似的思路。例如p串为ababaca，t串为abababacaba。用输入字符串的后缀和p串进行匹配。

初始为匹配个数为0
输入a，匹配个数1
输入ab，匹配个数2
输入aba，匹配个数3
输入abab，匹配个数4
输入ababa，匹配个数5
输入ababab：匹配个数4（用p串和这个串的后缀进行匹配）
…

按照这个方法一直进行匹配，如果最终匹配个数是p串长度则成功匹配。

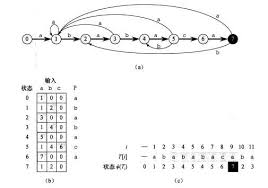
上图就是字符串匹配的状态转移图了。注意这里只有两个字母ab，如果是26个字母那么状态转移图将非常复杂。

左边是表示某个状态输入某个字符会转移到某个状态的图。例如状态5（ababa）输入b会进入状态4.

计算状态转移函数的方法

int m = p.size();
int number = 2;
int state[m][number];
for(int i=0; i<m; i++)
{
    for(int k=0; k<number; k++)
    {
        char c = (char)('a' + k);
        string sub = p.substring(0, i) + c;
        state[i][k] = match(sub, p);
    }
}

int match(string sub, string p)
{
    int suffixLen = 0;
    int k = 0;

    while(k < sub.length() && k < p.length()) 
    {
         int i = 0;
         for (i = 0; i <= k; i++) 
         {
             if (sub.charAt(sub.length() - 1 - k + i) != p.charAt(i)) 
             {
                   break;
             }
         }

         if (i - 1 == k) 
         {
            suffixLen = k+1;
         } 

         k++;
     }

     return suffixLen;
 }

kmp

可以看这篇