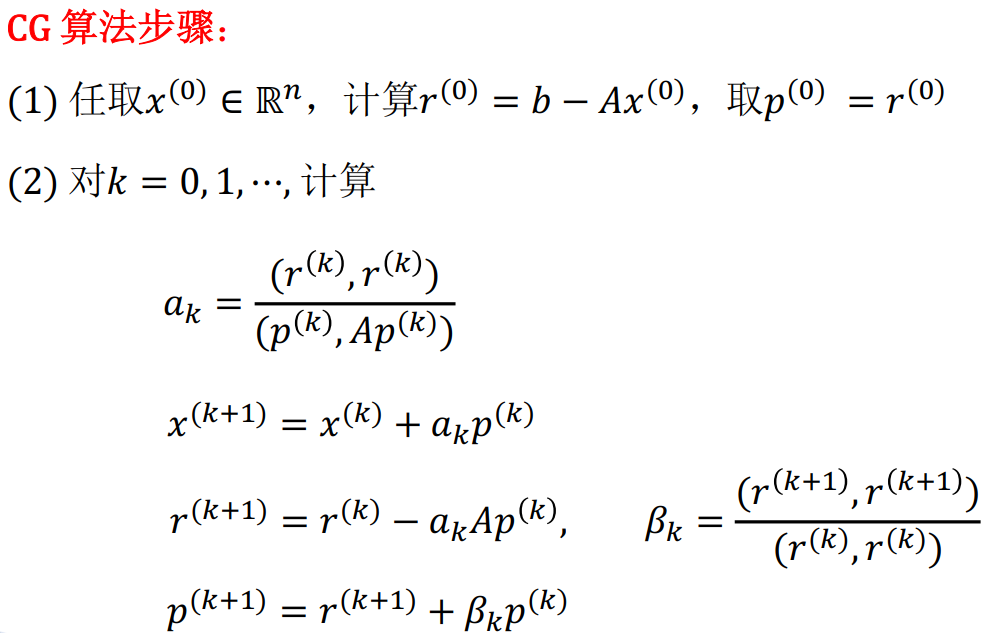矩阵求解

直接解法

高斯消去法

高斯消去法是先将矩阵变为上/下三角矩阵，然后使用回带法进行求解，例如

$$\begin{bmatrix} 1 & 1 & 1 & 6\\ 0 & 4 & -1 & 5\\ 2 & -2 & 1 & 1 \end{bmatrix}\overset{r_3 - 2r_1}{\rightarrow} \begin{bmatrix} 1 & 1 & 1 & 6\\ 0 & 4 & -1 & 5\\ 0 & -4 & -1 & -11 \end{bmatrix}\overset{r_3 - r_2}{\rightarrow} \begin{bmatrix} 1 & 1 & 1 & 6\\ 0 & 4 & -1 & 5\\ 0 & 0 & -2 & -6 \end{bmatrix}$$

因此$x_3 = 3 , x_2 = 2 , x_1 = 1$

$$\begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n}\\ 0 & a_{22} & \dots & a_{2n}\\ \vdots & \vdots & & \vdots\\ 0 & a_{n2} & \dots & a_{nn} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix}$$

然后要把第二列消0，也就是后面的行都减去第二行的$\frac{a{i2}}{a{22}}$倍。

最终的公式为：

$$\left\{\begin{matrix} m_{ik} =& a_{ik}^{(k)} & / & a_{kk}^{(k)}\\ a_{ij}^{(k+1)} =& a_{ij}^{(k)} & - & m_{ik} a_{kj}^{(k)}\\ b_i^{(k+1)} =& b_i^{(k)} & - & m_{ik} b_k^{(k)} \end{matrix}\right.$$

其中k代表当前处理第k行

求出上三角矩阵后进行回代计算

$$\left\{\begin{matrix} x_n =& b_n^{(n)} / a_{nn}^{(n)}\\ x_i =& (b_i^{(i)} - \sum_{j=i+1}^{n} a_{ij}^{(i)} x_j ) / a_{ii}^{(i)} \end{matrix}\right.$$

因为里面有除法，因此主对角线上的元素不能为0。但是由于可以做初等行列变换，因此实际的要求是顺序主子式都不为0。

第一个顺序主子式是$a{11}$,第二个顺序主子式是$a{11}, a{12}, a{21}, a_{22}$的行列式。

我们每次使用除法时是使用对角线元素作为分母，如果分母很小可能会导致最终误差较大，因此可以使用行列变换将该列的最大元素移到当前处理行，称为列主元消去法

三角分解

我们目标是求解Ax=b，其中A可以分解成L矩阵和U矩阵，也就是LUx=b.

其中L是一个下三角矩阵，U是一个上三角矩阵，设Ux=y,因此求解过程为：

1. Ly=b,求y
2. Ux=y,求x

$$A = \begin{bmatrix} 1 & & & \\ l_{21} & 1 & & \\ \vdots & \vdots & \ddots & \\ l_{n1} & l_{n2} & \dots & 1 \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & \dots & u_{1n}\\ & u_{22} & \dots & u_{2n}\\ & & \ddots & \vdots\\ & & & u_{nn} \end{bmatrix}$$

让LU矩阵相乘可以得到原矩阵，根据这个可以得到原矩阵和LU矩阵的转化关系。

• $u{1i} = a{1i} , l{i1} = a{i1}/u_{11}$
• $u{ri} = a{ri} - \sum{k=1}^{r-1} l{rk} u_{ki} i=r, r+1,\dots , n$
• $l{ir} = (a{ir} - \sum{k=1}^{r-1}l{ik}u{kr})/u{rr} , i=r+1,\dots ,n且r!=n$

然后再进行回代

迭代法

引例：求解方程 3x - $e^x$ = 0

首先将方程变形可得x = $e^x / 3$

然后令$x_0 = 0$，将$x_0$代入右边，可以得到一个值，这个值赋值给$x_0$，然后重复上述过程。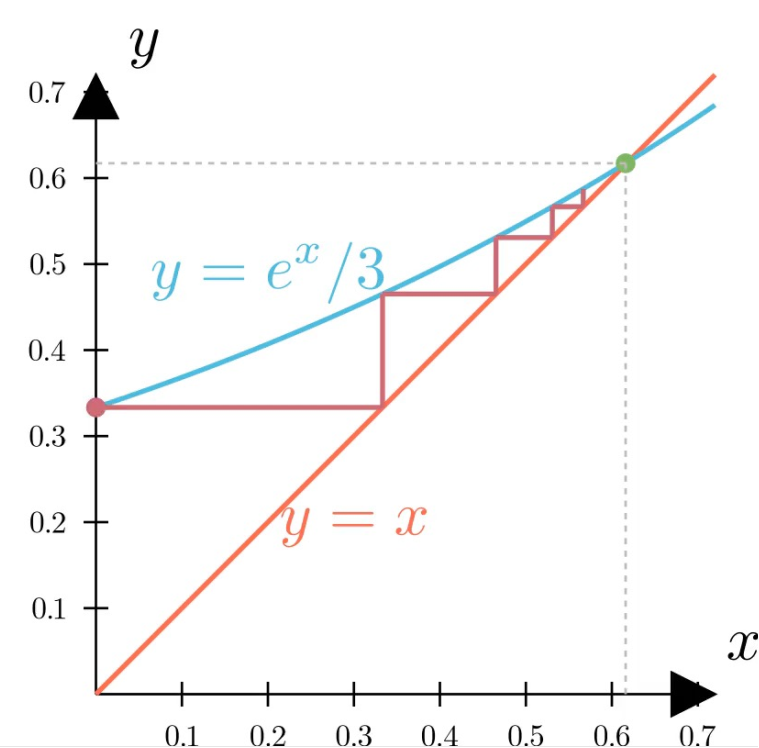

因为最终解是两条曲线的焦点，我们可以发现当$e^x / 3$大于x时会让x增大，反之会让x减小，最终会不断靠近真实解。

而对于方程组来说我们可以将Ax=b转化成x=Bx + f的形式，然后不断求解右边然后代入x直到误差小于某一个值。

总体流程为$(M - N)x = b => Mx = Nx + b => $x = M^{-1} N x + M^{-1} b$

迭代法敛散性

• 向量的极限：$\underset{k->\infty}{lim}a{ij}^{(k)} = a{ij}$，则称该向量序列收敛于A，记作$\underset{k->\infty}{lim} Ak = A$，其中$a{ij}^{(k)}$其实就是$A\times A \times A \dots A$的结果
• 矩阵的算子范数：$||A||_v = \underset{x \ne 0}{max} \frac{||Ax||_v}{||x||_v}$
• 矩阵的弗洛贝尼斯范数：$F(A) = ||A||F = (\sum{i,j=1}^{n} a_{i, j}^2 )^{\frac{1}{2}})$
• $||A||{\infty} = \underset{1 \le i \le n}{max}\sum{j=1}^{n} |a_{ij}|$
• $||A||1 = \underset{1 \le j \le n}\sum{i=1}^{n} |a_{ij}|$
• $||A||2 = \sqrt{\lambda{max} (A^T A)}$
• 三个命题等价
  • $\underset{k->\infty}{lim} B^k = 0$
  • $\rho (B) < 1$, $\rho(B)$是B的谱半径，谱半径也就是B最大的特征值
  • 至少有一种从属矩阵范数，使得$||B||_{\varepsilon}$ < 1

定理： 迭代法收敛的充要条件是矩阵B的谱半径$\rho(B) < 1$

定理2： 迭代法收敛的充分条件是某种算子范数||B|| < 1

雅克比，高斯-赛德尔迭代法

雅克比迭代法

将A分成D，L, U三部分，其中D是对角阵，L是下三角矩阵，U是上三角矩阵

(D-L-U)x = b => Dx = (L-U)x + b => x = $D^{-1} (L - U) x + D^{-1}b$

因为D是对角阵，因此它的逆就是对角元素的倒数，因此求解公式为：

$$x_i^{(k+1)} = (b_i - \sum_{j=1 , j \ne i}^{n} a_{ij} x_j^{(k)} / a_{ii}$$

高斯赛德尔

他和雅克比不一样的地方在于只将U矩阵移到了右边，也就是

(D-L-U)x = b => (D-L)x = Ux + b => $(D-L)x^{(k+1)} = U x^{(k)} + b => Dx^{k+1} = Lx^{(k+1)} + U x^{(k)} + b$

将$x^{(k+1)}$移到了右边看似让矩阵无法求解，但是由于L的特殊性让本次迭代时可以利用前面计算的信息

求解过程为：

$$x_i^{(k+1)} = (b_i - \sum_{j=1}^{i-1} a_{ij} x_j^{k+1} - \sum_{j=i+1}^{n} a_{ij} x_j^{(k)} / a_{ii}$$

• 严格对角占优矩阵： 如果$|a{ii}| > \sum{j=1 ,j\ne i}^{n}|a_{ij}|$,则称该矩阵为严格对角占有矩阵
• 弱对角占优矩阵：将上面的大于号替换成大于等于
• 可约矩阵： 如果存在一个置换矩阵P使得 $$P^T A P = \begin{bmatrix} A_{11} & A_{12}\\ 0 & A_{22} \end{bmatrix}$$

其中$A{11}和A{22}$都是方阵，则成为可约矩阵

如果A为强对角占优矩阵，或者A是弱对角占优不可约矩阵，则Ax=b的雅克比迭代法和高斯赛德尔迭代法收敛

超松弛迭代法

超松弛迭代法是在高斯-赛德尔迭代法上进行一些改进，它在$x^{(k+1)}$上添加了一些阻尼

$$x^{(k+1)} = x^{(k)} + \omega \Delta x^{(k)} = (1-\omega ) x^{(k)} + \omega x^{(k+1)}$$

如果$\omega > 1$，则成为超松弛迭代

而他的计算式为：

$$x_i^{(k+1)} = (1 - \omega ) x_i^{(k)} + \omega (b_i - \sum_{j=1}^{i-1} a_{ij} x_j^{(k+1)} - \sum_{j=i}^{n} a_{ij} x_j^{(k)}) / a_{ii}$$

要注意后面一个是$j = i$而不是$j = i + 1$

最速下降和共轭梯度

首先定义优化函数

$$\phi (x) = \frac{1}{2} (Ax, x) - (b, x) = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n} a_{ij} x_i x_j - \sum_{j=1}^{n} b_j x_j$$

而我们可以证明$x^$为Ax=b的解的充要条件是$\phi (x^ ) = \underset{x \in R^n}{min} \phi (x)$

因此我们将目标从求解Ax=b转向了优化$\phi (x)$

最速下降法

使用梯度下降法$x^{(1)} = x^{(0)} + \alpha p^{(0)}$，并且最速下降法要求

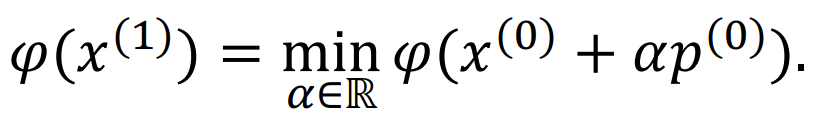
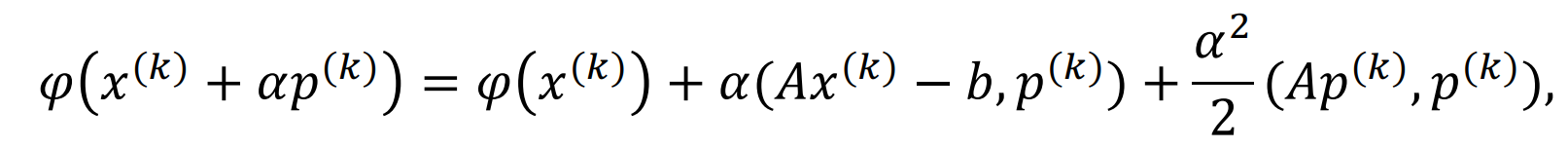
而我们对$\alpha$求导=0可得$\alpha_k = -\frac{(Ax^{(k)}-b, p^{(k)})}{(Ap^{(k)}, p^{(k)})}$

由于$p^{(k)}%是下降方向，我们知道沿负梯度方向下降下降速度最快，而这个函数的梯度为$Ax-b$,因此可以得知$p^{(k)} = b - Ax = r(k)$

因此

$$\alpha_k = \frac{(r^{(k)}, r^{(k)})}{(Ar^{(k)}, r^{(k)})}\\ x^{(k+1)} = x^{(k)} + \alpha_k r^{(k)}$$

但是当r很小时可能会出现舍入误差导致计算不稳定。

共轭梯度法

共轭梯度法的关键在于在$p^{(k)}$上添加了一些阻尼，也就是下面式子中的$\beta$