贝叶斯定理

定理： $P(H | X) = \frac{P(X | H) * P(H)}{P(X)}$

其中P(H | X)可以读作x条件下p的概率。

这个公式的意义在于我们可以使用先验概率来求解后验概率。例如：

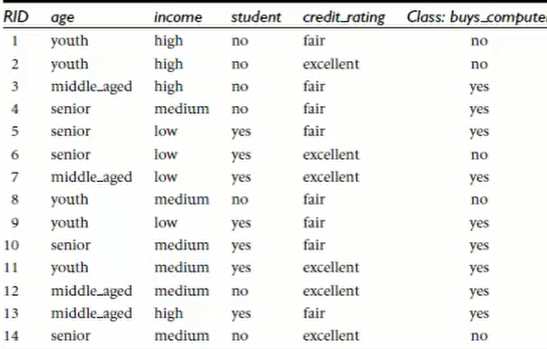
上面的例子中，买不买电脑是我们想知道的。而给出一个新的样例，我们不知道他买不买电脑，但是我知道它的年龄，收入等其他信息，现在我需要根据这些信息推断它买不买电脑也就是P( buys - computer = "yes" | age ="<=30")(小于30的人买电脑概率有多大)

朴素贝叶斯归纳方法

朴素贝叶斯就是各个属性之间相互独立。有一个数据样本集，每个样本是一个n维向量X＝（x1, x2, …xn）有m个类：C1, C2, …Cm；每个样本唯一的归属于一个类。

如果现在来了一个未知类别的数据X，想要求得它的分类，也就是P(H | X) H $\in$ {C1, C2, …, $C_m$}，可以写为P($C_j$ | X)$

依照贝叶斯定理，可得$P(C_j |X) ＝ P(X|C_j) P(C_j )$，由于P(X)是定值，所以P(X)可以省略。P(x | $C_j$)和P($C_j$)都可以求得，现在就可以求出$P(C_j | X)$的概率了。

其中P(x |$Cj$) = $\prod{i=1}^n p(x_i | C_i )$.

计算过程：

计算 P(C1), P(C2)等
计算$P(x_1 | C_1 ), P(x_2 | C_2 )$ …
计算$P(X | C_1 ), P(X | C_2)$ …
计算$P(C_1 | X), P(C_2 | X)$ …

以上面为例

希望分类的未知样本为
X=( age =“≤30”, income =“medium”, student = “ yes”, credit - rating = “fair")
要求计算出
P(buys - computer =“yes”| X)
和P(buys - computer = "no”| X)

计算过程如下

1.
P( buys - computer =“ yes”)=9/14 =0.643;
P(buys - computer ="no”)=5/14=0.357。

2. 
P(age =“< = 30”| buys - computer = "yes")=2/9= 0.222;
P( age =“< =30"| buys - computer ="no")=3/5= 0.600;
P(income="medium" | buys-computer ="yes")=4/9= 0.444;
P( income ="medium" | buys - computer ="no") =2/5= 0.400;
P( student ="yes" | buys - computer ="yes") =6/9= 0.667;
P( student = "yes" | buys - computer ="no")=1/5= 0.200;
P(credit - rating ="fair" | buys - computer ="yes")=6/9= 0.667;
P(credit - rating ="fair" | buys - computer ="no")=2/5=0.400。

3. 
P( X | buys - computer ="yes" ) =
0.222 ×  0.444 × 0.667 × 0.667 = 0.044;
P(X | buys - computer = "no") =
0.600 × 0.400 × 0.200 × 0.1400 = 0.019。

4. 
P( buys - computer = " yes " | X) =
    P(X | buys - computer = " yes " ) x 
    P( buys -computer = " yes " ) = 0.044 × 0.643 = 0.028;
P( buys - Computer = " no " | X) = 
    P(X | buys - computer = " no " ) × 
    P ( buys -computer = " no " ) =0.019 ×0.357 =0.007。
所以最终预测会买