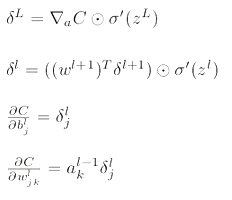RNN

RNN的特点是上一次输入会对下一次产生影响，相当于有了记忆功能，常用于自然语言处理。

这是RNN的结构图，它与传统神经网络的区别是在隐藏层有了一个循环。

这张图的含义是每一个时间点都可以有输出o，也可以没有。每一个时间点隐藏层输出作为下一个隐藏层的输入，也就是说该次训练对下一次训练会产生影响。

网上演示的时候隐藏层只有一层，这里就以一层为例。

隐藏层计算：

z(h)(t)=U⋅x(t)+W⋅s(t−1) #s(t-1)是前一刻隐藏层输出
s(t)=fh(z(h)(t))

s(t)是隐藏层输出， fh是激活函数，一般使用tanh或LeRu。

输出层使用softmax函数进行转换，然后损失函数使用交叉熵

Lt=−∑（N， i=0）yi(t)log(oi(t))

其中yi是真实值，oi是预测值

BPTT

BPTT是RNN所使用的反向传播算法。它和传统反向传播算法的区别是它还要照顾到W（前一层到这一层的权重）

大体上还是使用这四个式子

δk(t) 表示t时刻损失函数对output layer 节点的输入zk(t)的导数（也就是求上面方程中第一个式子）。

δk(t) = o(t) - 1

所以∂Lt \ ∂V = (o(t) - 1) * s(t)

δk(h)(t) = [δ(o)(t) ⋅ Vk] ∙ [1 − sk(t)^2]

所以 ∂Lt \ ∂U = δ(h)(t) * x(t)

向w传播的 δ(h)(t−1)=[δ(h)(t)⋅W] ∙ 1−s(t−1)^2和W)

∂Lt \ ∂W = δ(h)(t) * s(t-1)

LSTM

RNN的缺陷是会出现梯度消失现象，因此无法保存长时间记忆。LSTM通过两条记忆途径使得可以保存长时间记忆。

这是LSTM的结构图，其中上面那一条线代表长时间记忆，下面那一条代表短时记忆。而保存在尝试记忆中的信息由几个门控制。

这是第一个门控忘记门，用来剔除不重要的信息。至于为什么能忘掉不重要信息，只能说这是神经网络自己决定的（没找到解释）。如果某一项为0代表舍弃，为1代表全部保留。

公式中Wf⋅[ht−1,xt] = Wfh * h(t−1) + Wfx * xt。wf可以看成是两个矩阵拼接而成，然后对应和输入相乘。

记忆门，这个门决定我们要记忆什么，前一部分是删去要舍弃的记忆，后面一部分是加上要记住的东西。注意Ct是tanh

？： sigmoid函数和tanh函数意义

更新长期记忆。

输出门。更新ht并输出。之所以$C_t$需要用tanh是为了把它限制在(-1, 1)之间。最终我们需要的是$h_t 和 C_t$

虽然图中传递到下一层，实际上只是时间的不同，各个门的参数实际上还是同一个（虽然在不断更新）。和普通的神经网络不同之处在于他把上次的结果用于下次输入。

反向更新

首先确定更新内容。我们要更新四个b，四个w。其中w又要拆分成两部分，所以总共更新12个量。

δTo,t=δTt⨀tanh(ct)⨀ot⨀(1−ot)
δTf,t=δTt⨀ot⨀(1−tanh(ct)2)⨀ct−1⨀ft⨀(1−ft)
δTi,t=δTt⨀ot⨀(1−tanh(ct)2)⨀ct^⨀it⨀(1−it)
δTc^,t=δTt⨀ot⨀(1−tanh(ct)2)⨀it⨀(1−c^2)

yt=σ(Vht+by) // 当前状态输出
δt=∂E \ ∂ht = Vσ`

∂E \ ∂Woh,t = δo,t * h(t−1)
其他三个 同理

∂E \ ∂bo,t = δo,t
其他三个同理

∂E \ ∂Wox = δo,t * xt

反向更新具体过程可看

GRU

GRU相比于LSTM所花的时间更短，但是达成的效果差不多。

可以看到GRU只有一个参量要传递给下一个单元，并且需要更新的量也减少。

$R_t = \sigma (W_r * [H(t-1) \, X_t]) +b_r\\ Z_t = \sigma (W_z * [H(t-1) \, X_t]) + b_z$

这是重置门和更新门的计算公式，和LSTM计算方法相同，实际上GRU借鉴了LSTM的思想。但是这里只有一个额外的输入H(t-1)

⊙表示矩阵中对应元素相乘

$H_{t}^{'} = tanh(X_t * W_{xh} + (R_t ⊙ H(t-1)) * W_{hh} + b_h )\\ H_t = Z_t ⊙ H(t-1) + (1 - Z_t ) ⊙ H_{t}^{'}$

最后的zt和1-zt决定要记住新内容多还是老内容多，例如 zt=1/3, 那么老内容一次运行就只剩下1/3.($Z_t$实际上是一个矩阵，也就是上面的）

部分图片和思路出自