回溯法

回溯法概念

回溯法是一种能避免不必要搜索的穷举式算法，适用于一些解空间相当大的问题。

它经常呈现一种树形结构，先进入左节点，当到了底部或者条件不满足时返回父节点并进入右节点。一个典型的例子就是深度优先搜索

如果不加限制条件直接搜索的话复杂度将是2^n。因此我们需要添加一些限界函数来减小搜索量。

限界函数一般有两个，一个是用来限制左支的，叫显式约数条件。另一种是限制是否搜索右支的，叫隐式约束条件。

n叉树模板：

实例

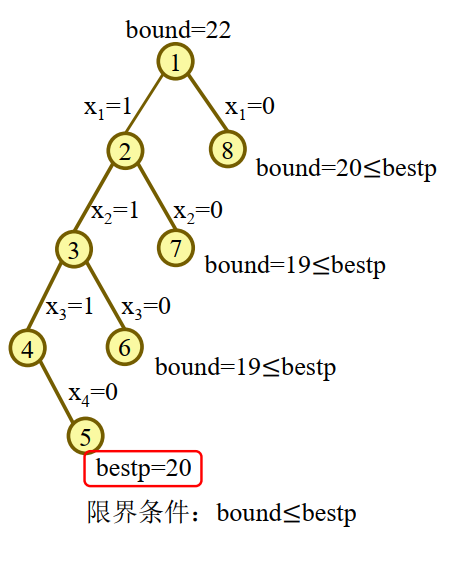
01背包问题

01背包问题最常见的办法是动态规划算法.这里介绍回溯法求解

  1. 将物品按密度进行排序
  2. 设bestp是当前最好收益并初始化为负无穷
  3. 设bound = cp+r是效益值的上界。其中cp是这个节点的收益值，r是剩下所有物品的连续背包问题收益值（也就是说不满一件也可以装进去）
  4. 展开左子节点：
    • 如果, 则装入k,且cw += Wk, cp += pk Xk = 1(说明这个节点使用了）
  5. 否则展开右节点：
    • 如果bound <= bestp。则停止展开右子树（就算把剩余物品都放进去也抵不上它的收益）。否则就 xk = 0,然后继续搜索

货箱装船问题

问题：给定载重量为 c 的货船，找一种装船的方法，使得装载的货箱数目最多。

分析

设cw是已装载货物重量

显式限界条件： 如果cw+w(i) > maxw 则杀死该左节点。
隐式限界条件： 如果cw+r <= bestw，则停止展开右节点。r是剩余货物的重量。

分支限界法

分支限界法也是一种穷举搜索算法。但是同样可以通过限界函数进行限界。一个典型例子就是广度优先搜索。

旅行商问题

首先说一下归约矩阵。

  • 行规约矩阵：找到每一行最小的数，然后让这一行都减去最小的数。
  • 行规约数： 每一行最小的数求和
  • 归约矩阵： 每一行做归约后每一列再做归约。归约数就是行规约数加上列归约数

归约矩阵的性质：

  • 每一行每一列都必须有一个0
  • 对于旅行商问题， 它的结果就是在归约矩阵中得到的结果加上归约数 W(f) = w’(f)+h

例：

其中q12表示A’矩阵中第一行第二列的点，表示我们要先从1到2.

之后的h’表示去掉这一行这一列和qji为无穷后的矩阵的归约值。因为我们到过这个节点之后这一行这一列都不会再有点了，所以可以去掉。另外如果不是导数第二个节点的话也不可能回到起点。

找到$\delta(i)$的最小值后以这个点作为起始点除去这一行这一列进行下一步搜索。

现在$\delta(4)$最小，所以$\delta(4)(1)$变成$+\inf$并且将第四行提到第一行，之后重复上述过程。

之后一直重复上述步骤直到搜索完成。

使用行规约矩阵的目的在于提前知道一些信息来进行分支限界。