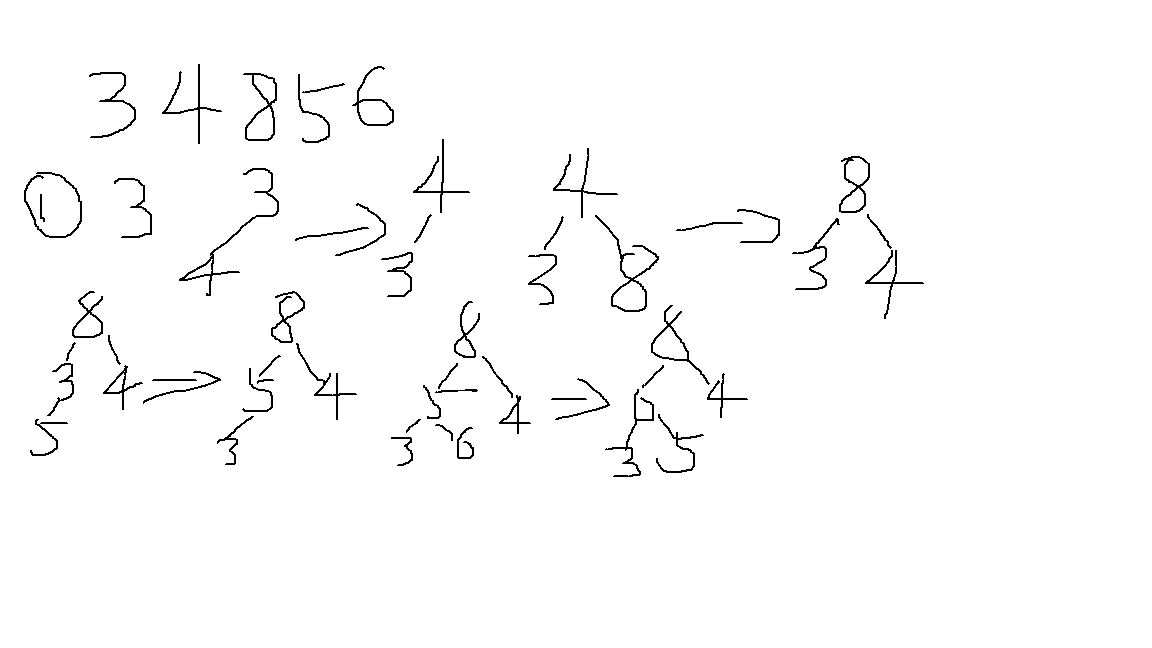插入排序
稳定？不稳定： 稳定指的是两个相同的元素排序完成之后在表中相对位置不变。
直接插入
当插入第i个时，前i-1个已经排好了。
int tag = 0;
for(int i=1; i<n; i++)
{
if(a[i]<a[i-1])
{
tag = a[i];
int temp;
for(int k=i-1; k>=0; k
{
if(a[k]>tag)
{
a[k+1] = a[k];
temp = k;
}
else
{
break;
}
}
a[k+1] = tag;
}
}
|
默认第一个已经排好，从第二个开始从后往前排，如果第k个数比要比较的数大就把这个数往后排。
复杂度： n^2
折半插入
折半排序基于前面的直接插入，不同的是它通过二分找插入位置。然后再移动
int tag = 0;
for(int i=1; i<n; i++)
{
tag = a[i];
int low=0, high=i-1;
while(low<=high)
{
int mid = (low+high)/2;
if(a[mid]>tag)
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}//high+1是插入位置
for(int k=i-1; k>=high+1; k--)
{
a[k+1] = a[k];
}
a[high+1] = tag;
}
|
复杂度 n^2
希尔排序
思想： 把序列按gap划分成若干个子序列。例如有6个元素，gap是3，那么第0个和第3个是一个序列，第1个和第4个是一个序列。之后在每个子序列中直接插入。然后折半缩小gap。
第一个gap一般取n/2。
int gap = n/2;
int tag = 0;
while(gap != 0)
{
for(int i=gap; i<n; i++)//从gap开始是因为直接插入排序中默认第一个已经排序
{
tag = a[i];
int temp;
for(int k=i-gap; k>=0; k-=gap)
{
if(a[k]>tag)
{
a[k+tag] = a[k];
temp = k;
}
}
a[temp+tag] = tag;
}
gap /= 2;
}
|
复杂度：n(longn)^2。但这是一种不稳定的排序
起泡排序
起泡排序是过程是逐个比较，比较出最小的放到第一个，然后放到第二个。
int flag=0,exchange=0;
while(flag<n-1 && exchange==0)
{
exchange = 0;
for(int i=n-1; i>flag; i--)
{
if(a[i-1]>a[i])
{
a[i-1] = a[i] ^ a[i-1];
a[i] = a[i] ^ a[i-1];
a[i-1] = a[i] ^ a[i-1];
exchange = 1;
}
//这一步后小的在前面，然后下一次又是把i-1和i-2比，如果i-1小，又跑到前面
//这样第i-1个一直是最小的（相对于它后面的元素）
}
flag++;
}
|
复杂度 n^2
快速排序
以前的一篇
选择排序
直接选择排序
这个就不多说了。
int min = 2147483647;
int tag = 0;
for(int i=0; i<n-1; i++)
{
for(int k=i+1; k<n; k++)
{
if(a[k]<min)
{
min = a[k];
tag = k;
}
}
swap（a[i], a[tag]);
}
|
堆排序
堆排序是完全二叉树产生的数组。然后建立一个父节点比子节点大/小的数组。父节点比子节点大的叫大顶堆，父节点比子节点小的叫小顶堆。
假设父节点是i，那么两个子节点分别是i2和i2+1。下标要从1开始
过程，以小顶堆为例
- 初始化，首先构造一个大顶堆，过程是用这个节点和它的父节点进行比较，如果小就交换位置，然后再和新位置的父节点进行比较。先拿第一个数和第二个数进行比较，如果第一个数比第二个数小那个交换位置。然后第三个数和第一个数比较。此外，还可以从小到大直接建
之后第4个数是插入到第二个数上的，就拿第四个数和第二个数比较，如果第四个数比第二个数小就把第二个数往上提，之后再和第一个数进行比较。然后依此类推。
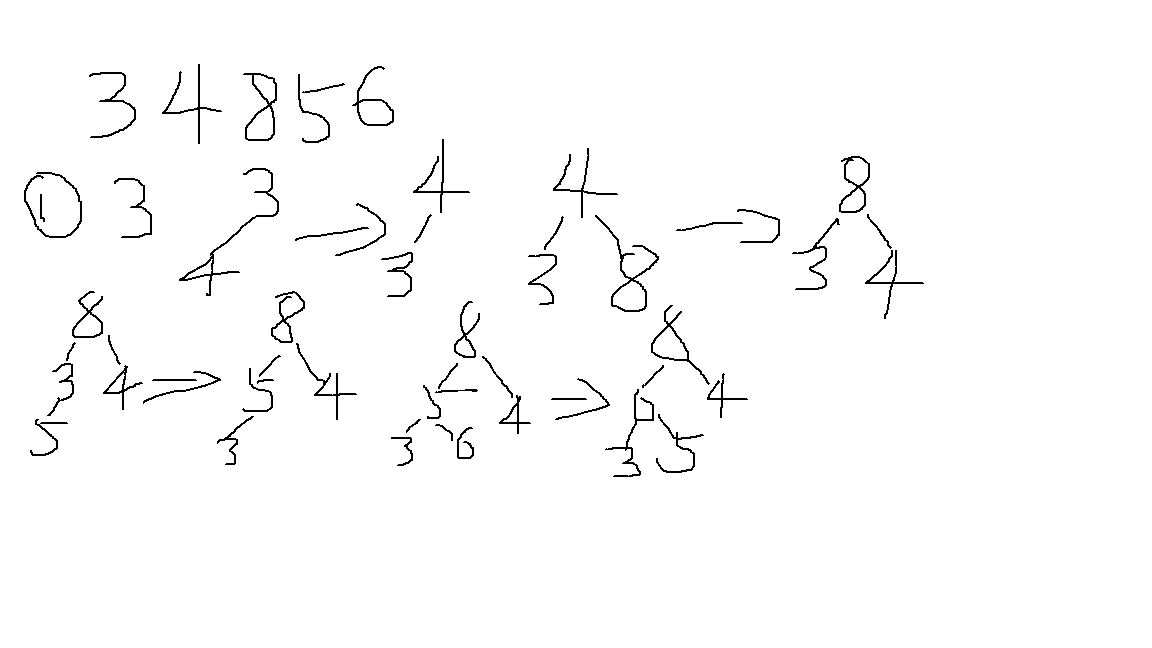
- 把第一个元素和最后一个元素进行交换，然后对前n-1个元素进行处理。开始我们建立的是大顶堆，现在我们把最大的放到后面就变成小顶堆了。并且这时不仅满足小顶堆，还满足左儿子一定比右儿子小。
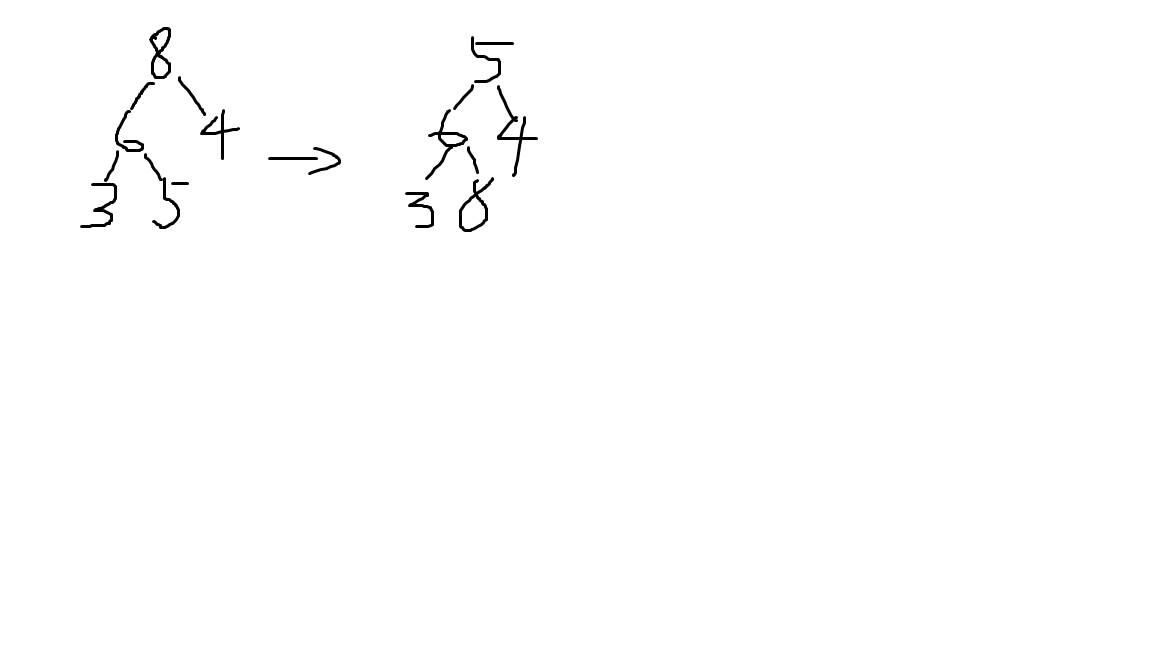
- 之后就是用根节点左右儿子中比较大的节点和根节点进行比较。然后如果比根节点大就进行换位。然后再在新位置和新的子节点进行比较。完成之后又把根节点放到最后。之后就重复第二步和第三步。（不画图了，难死我了）
//根据上面自己写的，拿过几个数据代过，如果想看更标准的可以看下面模板(饶命)
void Heap(int *a, int n)
{
for(int i=n/2; i>=1; i--)
{
int now = i;
while((now<<1) <= n)
{
int largest ;
int l = now << 1;
int r = (now<<1)+1;
if((now<<1)+1 == n)
{
if(a > a)
{
int temp = a;
a = a;
a = temp;
}
break;
}
if(a > a)
{
largest = l;
}
else
{
largest = r;
}
if(a > a)
{
int temp = a;
a = a;
a = temp;
now = largest;
}
else
{
break;
}
}
}//初始化
for(int i=n; i>1; i--)
{
a = a ^ a;
a = a ^ a;
a = a ^ a;
int now = 1;
while((now<<1) < i)
{
int big;
if((now<<1)+1 == i)
{
int temp = now<<1;
if(a < a)
{
a = a ^ a;
a = a ^ a;
a = a ^ a;
}
break;
}//只有左节点
if(a < a)
{
big = (now<<1)+1;
}
else
{
big = now<<1;
}
if(a > a)
{
a = a ^ a;
a = a ^ a;
a = a ^ a;
now = big;
}
else
{
break;
}
}
}
}
|
模板
#include <iostream>
int heapsize;
void MAX_HEAPIFY(int A[], int i)
{
int l = 2 * i;
int r = 2 * i + 1;
int largest;
if (l <= heapsize && A[l]>A[i])
largest = l;
else
largest = i;
if (r <= heapsize && A[r]>A[largest])
largest = r;
if (largest != i)
{
int tmp = A[largest];
A[largest] = A[i];
A[i] = tmp;
MAX_HEAPIFY(A, largest);
}
}
void BUILD_MAX_HEAP(int A[])
{
int i;
for (i = (int)(heapsize / 2); i >= 1; i--) {
MAX_HEAPIFY(A, i);
for (int j = 1; j <= 10; j++)
printf("%d ", A[j]);
printf("\n");
}
}
void HEAPSORT(int A[])
{
BUILD_MAX_HEAP(A);
int i;
int tmp;
for (i = heapsize; i >= 2; i--)
{
tmp = A[1];
A[1] = A[i];
A[i] = tmp;
heapsize--;
MAX_HEAPIFY(A, 1);
}
}
int main()
{
int A[11] = { 0, 5, 3, 2, 1, 4, 6, 9, 7, 8, 10 };
int n = sizeof(A) / sizeof(int) - 1;
heapsize = n;
HEAPSORT(A);
for (int i = 1; i <= n; i++)
printf("%d ", A[i]);
return 0;
}
|
复杂度： nlogn.但是不稳定
归并排序
以前博客