计算几何基础
判断两直线是否相交
P(x1,y1) Q(x2,y2) 两向量的叉积为 x1*y2-x2*y1
如果 $p\times q$>0 p在q的顺时针方向（右手螺旋定则）
$p \times q$<0 p在q的逆时针方向
=0 ，共线或反向
先做一次快速排斥实验，判断下一个线段中 x 较大的端点是否小于另一个线段中 x 较小的段点，若是，则说明两个线段必然没有交点，同理判断下 y
代码
max(C.x,D.x)<min(A.x,B.x) || max(C.y,D.y)<min(A.y,B.y) || |
如图所示，如果想判断两线段相交，只需要判断A 和 B在cd两侧即可
所以只需要 向量AD*CD与 BD*CD异号即可
如果端点正好在另一条线段上，两者乘积等于0
如果两者平行，叉积也为0但是可以在快速排斥实验中排除掉
总代码
struct Line { |
判断点是否在多边形内部
我们先将横纵坐标存在一个数组内
第一步if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) {
// 这个测试都过不了。。。直接返回false；
}
这个测试是画一个四边形
第二步， 这里我们就要讲一个定理了，以某一点为端点画一条射线，如果穿过图形次数为奇数次，则在图形内，如果是偶数次，在图形外
为了方便讨论，我们将以x轴正方向做一条射线
int pnpoly (int nvert, float *vertx, float *verty, float testx, float testy) { |
nvert 是 顶点数量，testx和testy是顶点横纵坐标
第一段的意思是
verty[i] <testy < verty[j]
或者
verty[j] <testy < verty[i]
这段代码是用来粗略判断射线是否会经过该边的（没考虑反向和端点）
第二段是用来判断测试点是否在两点连线之下，这里用了斜率（移下项）
c=!c;是用来判断奇数次还是偶数次的
多边形的面积
s=pow(p(p-a)(p-b)*(p-c),0.5),p=(a+b+c)/2
凸多边形都可以通过划分变成三角形
凸包
用最少的点把给出的点全部包住
andraw算法
把所有点按第一关键字x第二关键字y按从小到大排序，并且删除重复点，得到序列p1…pn
把p1 p2放入凸包中，凸包中的点用栈来保存
然后 p1p2和p2p3叉积，如果叉积大于0，则说明p1p2在p2p3右边，说明p3在内部，我们就不选，反之则把它拖入栈中并且要把p2拖出栈中
这样一直到pn算完成了一遍（下凸包），我们还要从pn反过来到p1（上凸包）,合起来就是完整的凸包
using namespace std;
struct point{
int x,y;
};
bool cmp(point a,point b)
{
if(a.y==b.y&&a.x<b.x)
return true;
else if(a.y<b.y) return true;
return false;
}
double dis(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(b.y-a.y)*(b.y-a.y));
}
bool xcross(point a,point b,point c)
{
return (a.x-c.x)*(b.y-c.y)>=(b.x-c.x)*(a.y-c.y);//斜率
}
point node[100005];
int num[100005];
int n;
int main()
{
scanf("%d",&n);
for(int i=0;i<n;++i)
{
scanf("%d%d",&node[i].x,&node[i].y);
}
sort(node,node+n,cmp);
num[0]=0; num[1]=1;
int top=1;
for(int i=2;i<n;++i)
{
while(top>1&&xcross(node[i],node[num[top]],node[num[top-1]]))
top--;
top++;
num[top]=i;
}
int basic=top;
for(int i=n-2;i>=0;--i)
{
while(top>basic&&xcross(node[i],node[num[top]],node[num[top-1]]))
top--;
top++;
num[top]=i;
}
double s;
s=0.0;
for(int i=1;i<=top;++i)
{
s+=dis(node[num[i-1]],node[num[i]]);
}
printf("%.1lf",s);
return 0;
}
旋转卡壳
旋转卡壳可以用来求凸包的直径，宽度，两个不相交凸包间最大距离和最小距离等
如果过凸包上的两个点可以画一对平行直线，使凸包上所有点都夹在两
条平行线之间 || 落在平行线上，那么这两个点称为一对对踵点。
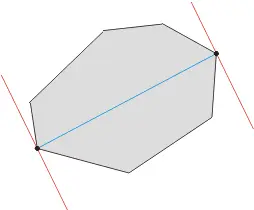
其实简单来说就是用一对平行线“卡”住凸包进行旋转。
被一对卡壳正好卡住的对应点对称为对踵点，对锺点的具体定义不好说，不过从图上还是比较好理解的。可以证明对鍾点的个数不超过3*n/2
卡壳有两种情况，第一种是一点对一点， 也就是上图中的
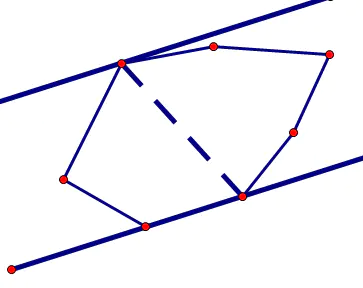
另一种是一边只有一点，另外一边有两个点
第二种情况中我们可以发现对鍾点到对应边的距离比其他的要大（不要问我为什么）
Step1：计算多边形 y 方向上的端点，称之为 ymin 和 ymax。
Step2：通过 ymin 和 ymax 构造两条水平切线，由于他们已经是一对对
踵点，计算他们之间的距离并维护一个当前最大值。
Step3：同时旋转两条直线到其中一条与多边形的一条边重合。
Step4：一个新的对踵点对此时产生，计算新的距离，并和当前最大值进
行比较，若大于当前最大值。则更新。
Step5：重复 Step3 和 Step4 的过程直到再次产生新的对踵点对。
Step6：输出最大直径的对踵点对。
听起来有点小麻烦，观察可以发现当平行线和多边形的一条边重合的时
候最会产生一对新的对踵点
这条边的两个端点和原来的点都可能更新最大值
不妨考虑找离每条边最远的点，显然，这条边的两个端点都和最远点是
对踵点
特殊情况，如果有两条边是平行的，必须考虑所有的对踵点。
旋转卡壳的均摊复杂度 O(n)，但这个问题需要求凸包，复杂度是
O(nlogn)
void solve2(int num) |