基础

上下文无关文法(CFG)是一些固定的语法知识，例如

S ->NP, VP 句子可以由动词词组和名词词组构成
NP->Det, Noun Det和Noun可以构成一个名词词组
VP->Verb, NP 动词词组可以由动词+名词词组构成
NP->eyes eyes是名词词组

通过这些规则我们可以找到一个句子的句法分析树。但是我们可能会找到非常多的句法分析树，并且没有办法判断到底使用哪一种。因此想到给每一个语法分配一个概率值。也就是概率上下文无关文法

S->NP VP 1.0
PP->P NP 1.0
VP->V NP 0.7
P->With 1.0
...

一些符号定义

  • G： 语法
  • L： 由语法生成的语言
  • t： 句法分析树
  • {}: 非终结符号集合，也就是NP，P等参数
  • {}: 终结符号集合，也就是实实在在的单词
  • : 句子序列

例如一个句子: astronomers saw stars with eyes,它的句法树可能为

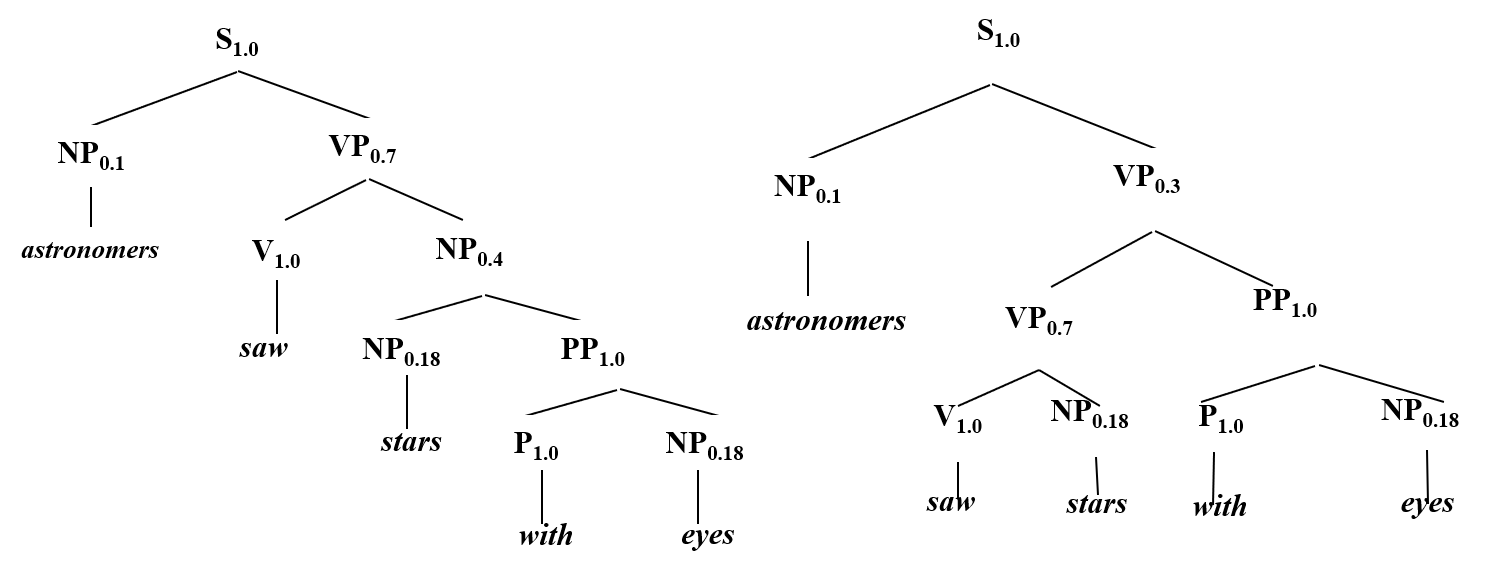
计算句法分析树的概率; $$\prod_{i=1..k}P(r(i))$$$。其中r(i)是CFG规则

计算句子概率

给定一种语法，如何计算这个句子出现的概率？

内部概率: .这是一种自底向上的方法，首先求单个单词的概率，然后求两个单词结合可能的情况。

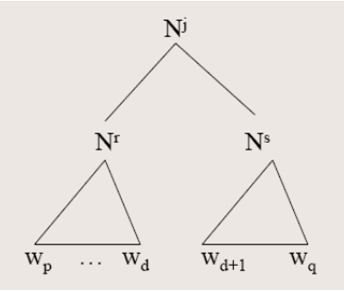
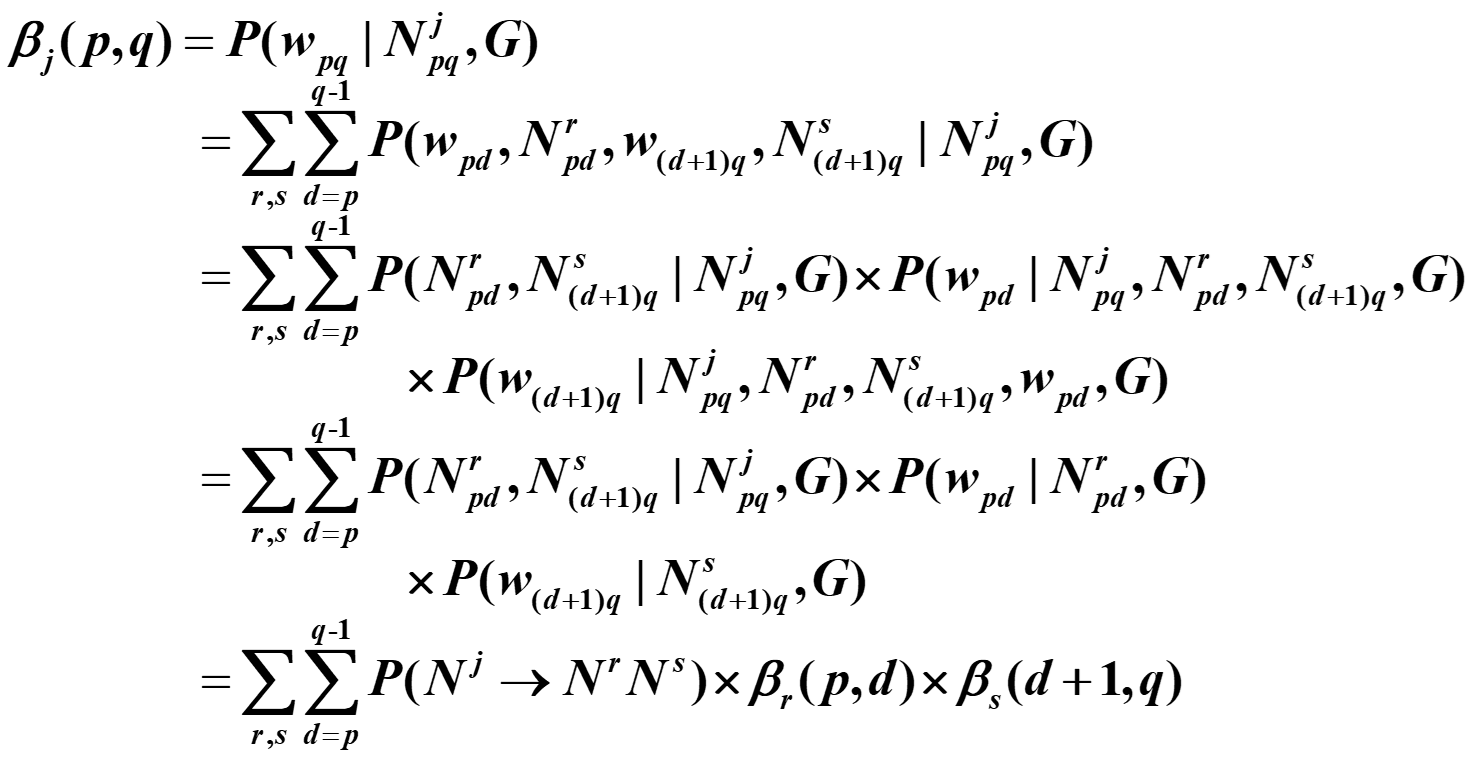
也就是说可以将这个文法分成两个小部分，然后计算两个小部分的概率及整合成整体的概率。

外部概率

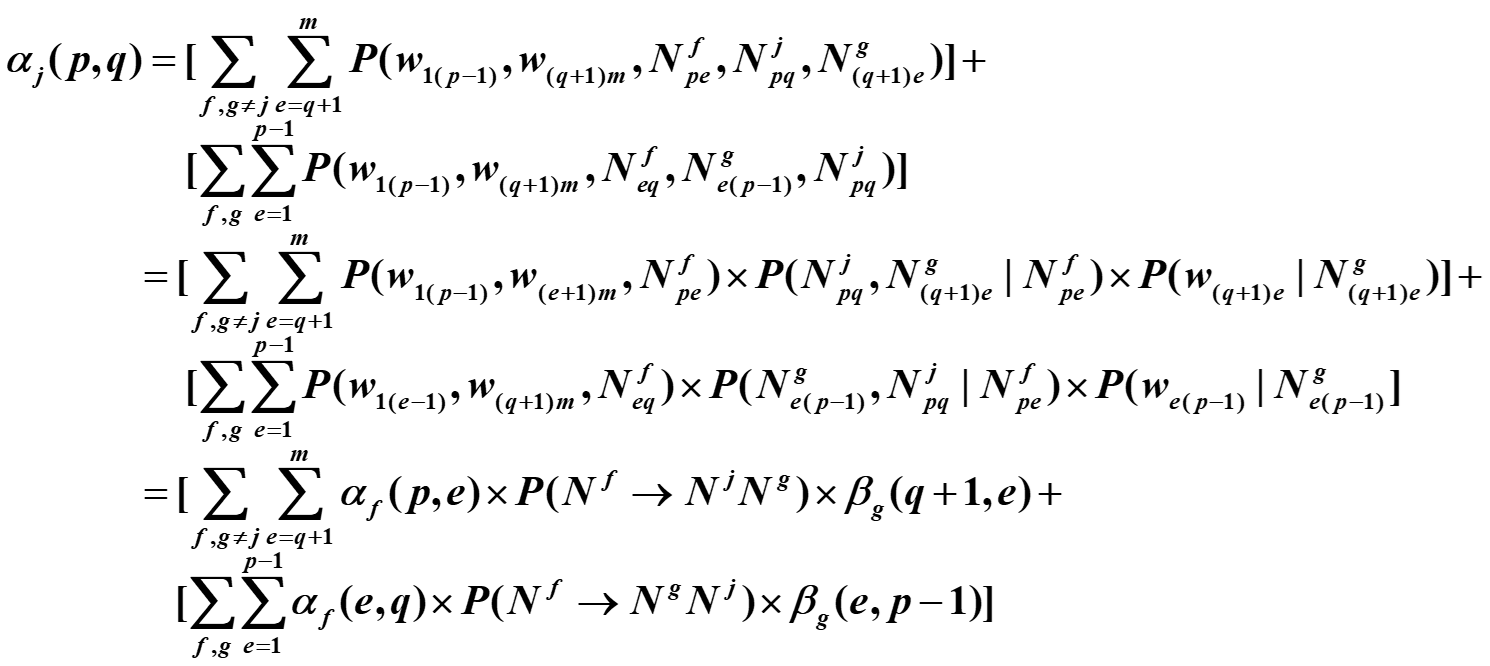
确定句子最佳分析树

基本做法和内部概率相似，但是这里我们不需要遍历，只需要找出所有可能中最大的。即