组合逻辑设计
组合电路和时序电路
- 组合电路： 由当前输入值决定输出值
- 时序电路： 由当前输入值和前一阶段的输入值共同决定输出
例如:
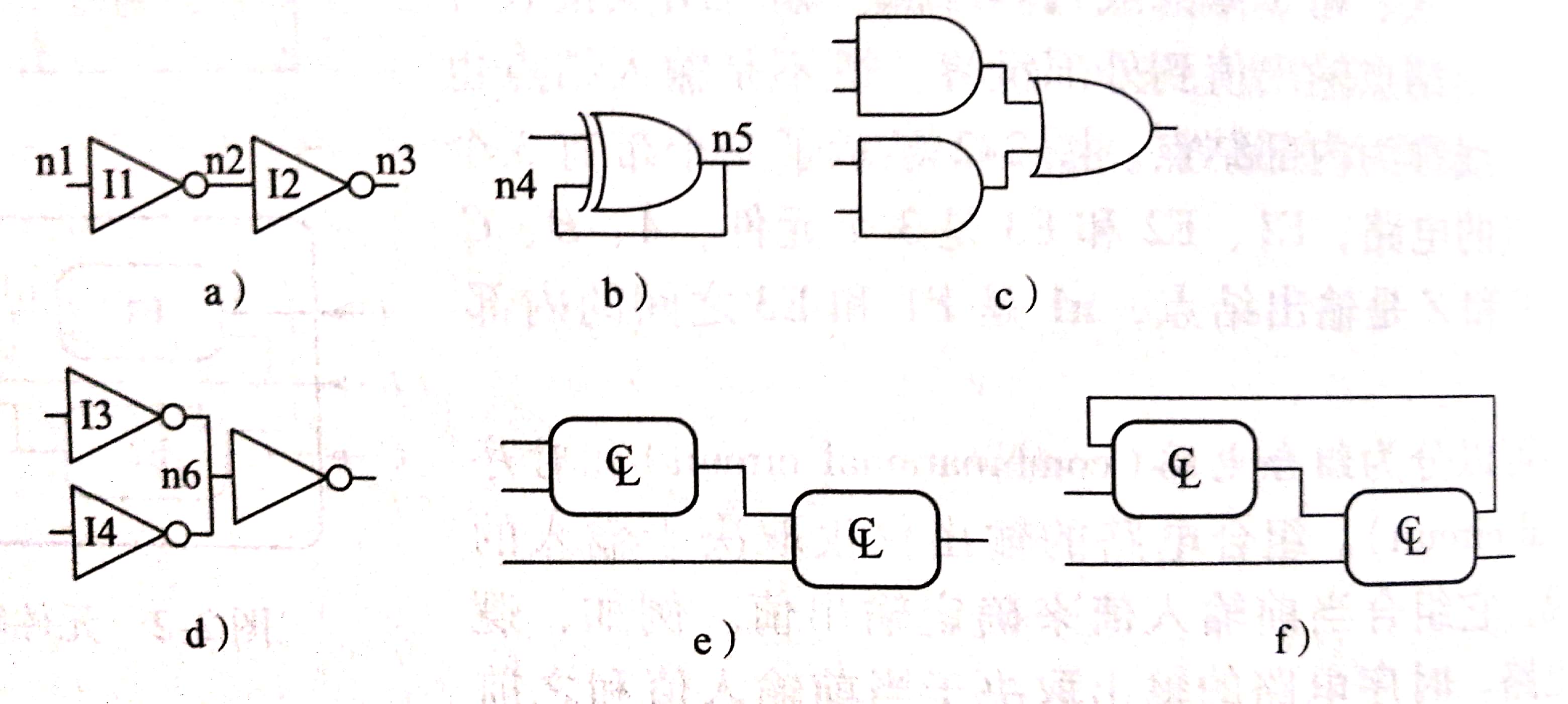
图b和图f属于时序电路，因为它的输出转化为了下一次的输入。图f中的符号是组合电路
图d是一个错误电路，因为到n6点可能会冲突
布尔表达式
一些术语：
*: 与符号，取交集，也叫相乘+： 或符号，取并集，也叫相加- 项： 变量或者它的反
- 最小项： 一个包含全部输入变量的乘积项。例如有三个变量A、B、C，则ABC是一个最小项（也就是 $A \cap B \cap C$), 而AB不是
- 最大项： 包含全部输入的和。 例如 A + B + C(也就是$A \cup B \cup C$)是一个最大项
- 蕴涵项： 多个项相乘
与或式与或与式
与或式
| A | B | Y | 最小项 | 最小项名称 |
|---|---|---|---|---|
| 0 | 0 | 0 | $\bar{A} \bar{B}$ | $m_{0}$ |
| 0 | 1 | 1 | $\bar{A} B$ | $m_1$ |
| 1 | 0 | 0 | $A \bar{B}$ | $m_2$ |
| 1 | 1 | 0 | A B | $m_3$ |
真值表每一项都和一个为 TRUE的最小项相关联，并且它的编号正好是AB的二进制值，例如AB = 10 则为$m_2$
只有当AB为真时对应的最小项才为真，其他都为假。例如只有当A = 0 ，B = 1时$\bar{A} B$才为真。
所有函数都可以写成有表中最小项相与所构成的表达式。例如 Y = $A\bar{B}$ + BA.由于这种先与后或的表达方式所以被称为与或式。
因此也可以使用最小项的序号进行表达，如 $F(A, B) = \sum (m_1 , m_3 ) = \sum (1, 3)$
如果给出了真值表那么可以唯一的用一个与或式表达，例如上面与或式为 $\bar{A} B$，因为只有在A为0，B为1时为真，其他都是0
也可以使用或与式进行表达：
可以看出与或式与或与式正好相反，编号相同的与或式和或与式互为反函数。
或与式
| A | B | Y | 最大项 | 最小项名称 |
|---|---|---|---|---|
| 0 | 0 | 0 | A + B | $ M_0 $ |
| 0 | 1 | 1 | A + $\bar{B}$ | $M_1$ |
| 1 | 0 | 0 | $\bar{A}$ + B | $M_2$ |
| 1 | 1 | 1 | $\bar{A} + \bar{B}$ | $M_3$ |
这里要求最大项输出为假
定理
| 编号 | 定理 | 编号 | 对偶定理 | 名称 |
|---|---|---|---|---|
| T1 | B * 1 = B | $T1^{‘}$ | B + 0 = B | 同一性定理 |
| T2 | B * 0 = 0 | $T2^{‘}$ | B + 1 = 1 | 零元定理 |
| T3 | B * B = B | $T3^{‘}$ | B + B = B | 重叠定理 |
| T4 | $\bar{\bar{B}} = B$ | 回旋定理 | ||
| T5 | B * $\bar{B}$ = 0 | $T5^{‘}$ | B + $\bar{B}$ = 1 | 互补定理 |
| T6 | B C = C B | … | B + C = C + B | 交换律 |
| T7 | （B C) D = B （C D） | … | (B + C) + D = B + (C + D) | 结合律 |
| T8 | (B C) + (B D) = B * (C + D) | … | (B + C) (B + D) = B + (C D) | 分配律 |
| T9 | B * (B + C) = B | … | B + (B * C) = B | 吸收律 |
| T10 | (B C) + (B $\bar{C}$) = B | … | (B + C) * (B + $\bar{C}$) = B | 合并律 |
| T11 | （B C) + ($\bar{B}$ D) + (C D) = B C + $\bar{B}$ * D | … | (B + C) ($\bar{B}$ + D) (C + D)= (B + C) * ($\bar{B}$ + D) | 一致律 |
| T12 | $\overline{B{0} * B{1} * …}$ = ($\bar{B{0}} + \bar{B{1}} …$) | … | $\overline{B{0} + B{1} … }$ = ($\bar{B{0}} * \bar{B{1}}$) | 的摩根定律 |
使用这些定律就可以将一些式子简化了
最小化式中最长使用的是$PA + P\bar{A} = P$来合并项。我们称使用了最少蕴涵项的等式为最小与或式。如果蕴涵项数量相同，那么具有最少项数的与或式是最小与或式。
例如最小化等式： $\bar{A} \bar{B} \bar{C} + A * \bar{B} \bar{C} + A \bar{B} C$
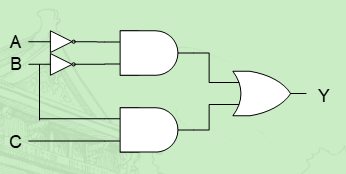
从逻辑到门
例如：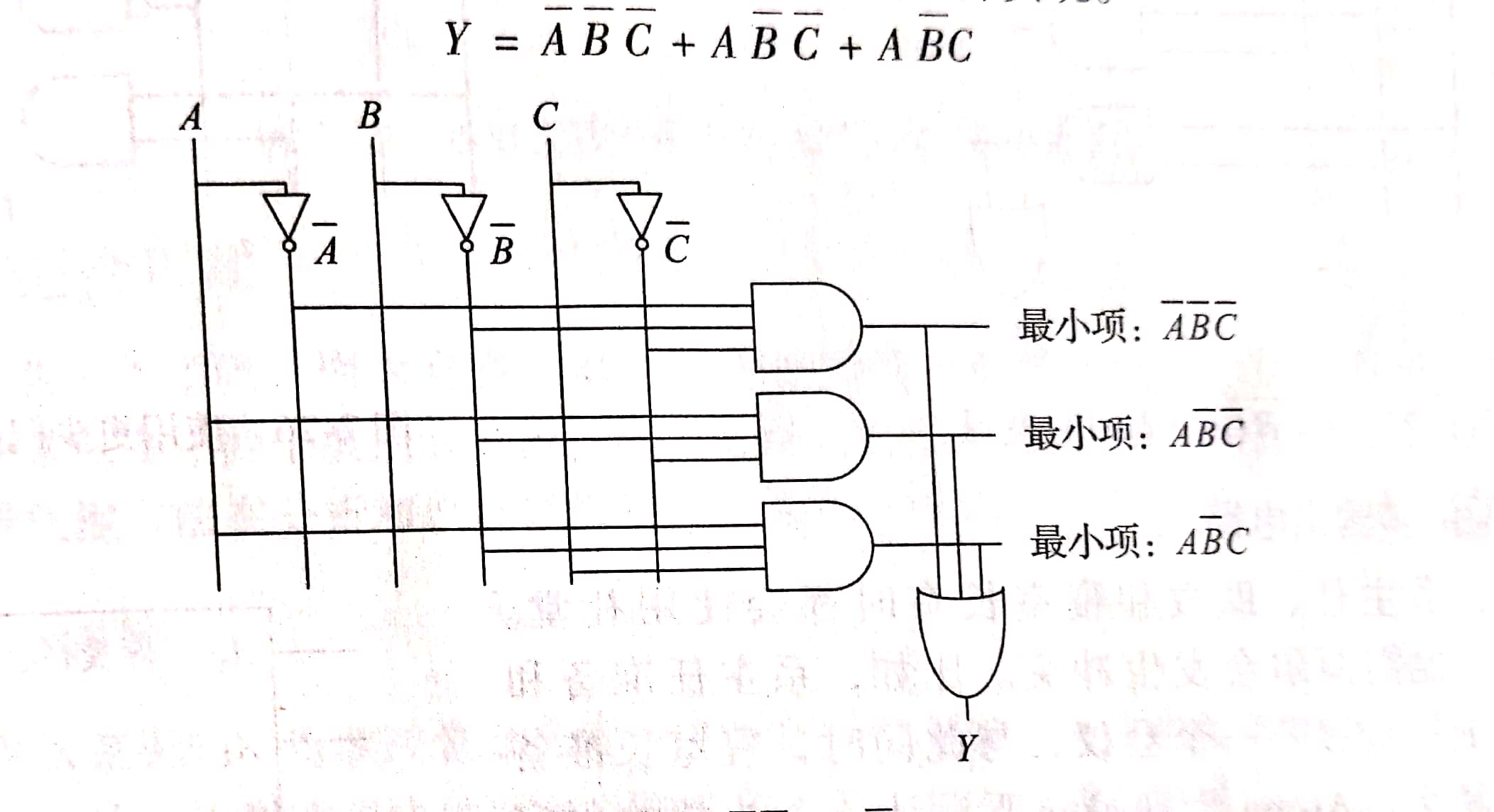
这种排线还是很清晰的。为了便于观察，画图时最好遵循以下规范
- 输入在左边（或上面）， 输出在右边（或下面）
- 门从左往右流
- 最好用直线
多级逻辑
减少硬件
例如：
这是一个三输入的异或门（异或又叫半加法，即不进位的加法，因此有奇数个1输出为1），可以看到里面使用了30个MOS晶体管（与门或者是或门需要6个晶体管）。
如果我们使用两个异或器件就可以减少到20个晶体管（异或最好的实现需要10个晶体管）
一个极端的例子是8输入的异或。这意味着我们需要128个8输入与门和一个128输入的或门，这是不可想象的。但是可以把它变成三级异或。
推气泡
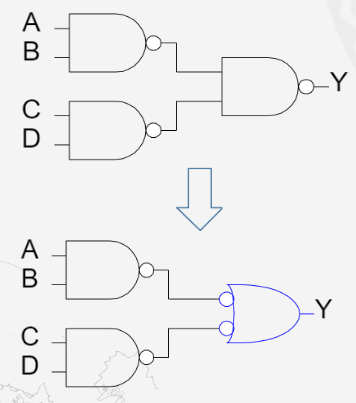
例如：
这个其实是异或操作。$\overline{AB} = \bar{A} + \bar{B}$,之后那两个气泡又可以抵消变成了我们常见的先与后或。但是这种只需要与非就可以完成并且比先与后或少用了晶体管。
x 和 z
x
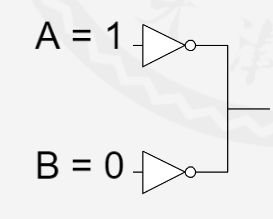
x表示未知或非法值，这通常表现在0和1汇合到一起的时候。
除此之外，他还可以用来表示无关项，也就是这个输入是0是1对输出没有影响。例如：
z
z表示浮空值，高阻值，也叫开路、短路等。常见的产生浮空的原因是忘记将输入端接入电压（这时一般是0，但是如果什么东西接触就可能导致1），但是这并不代表浮空值一定是0，他可能是0或1，也可能是非法值。
他和c语言中的分配出一块内存空间但是却没有指针指向它类似，虽然其中有一个值但是我们无法进行操作。
浮空值的一个应用是三态缓冲器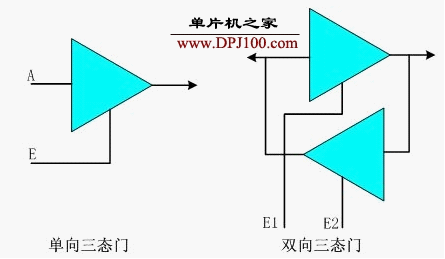
它的真值表为：
| E | A | Y |
|---|---|---|
| 0 | 0 | Z |
| 0 | 1 | Z |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
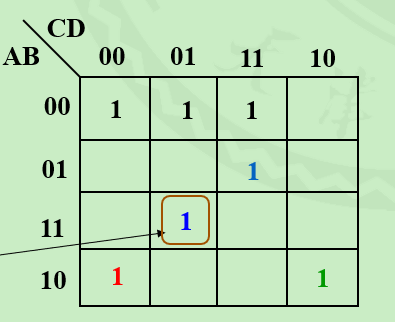
卡诺图
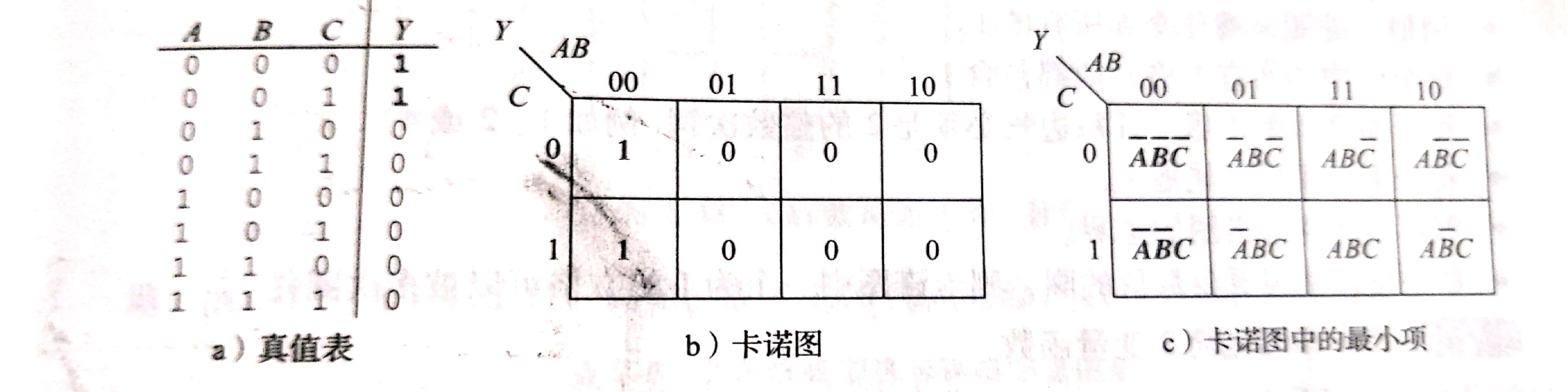
右边的就是一个卡诺图了。这里注意AB的顺序是00、 01、 11、 10而不是10、11。这种编码方式称为格雷码。
格雷码和普通的编码不同在于相邻元素只有一个变量不同并且起始元素和最后一个元素也只有一个变量不同，例如01和11只有第二个1不同，但是如果是00、01、10、11其中01和10就有两个不同了。
我们来看三个格雷码的构造：
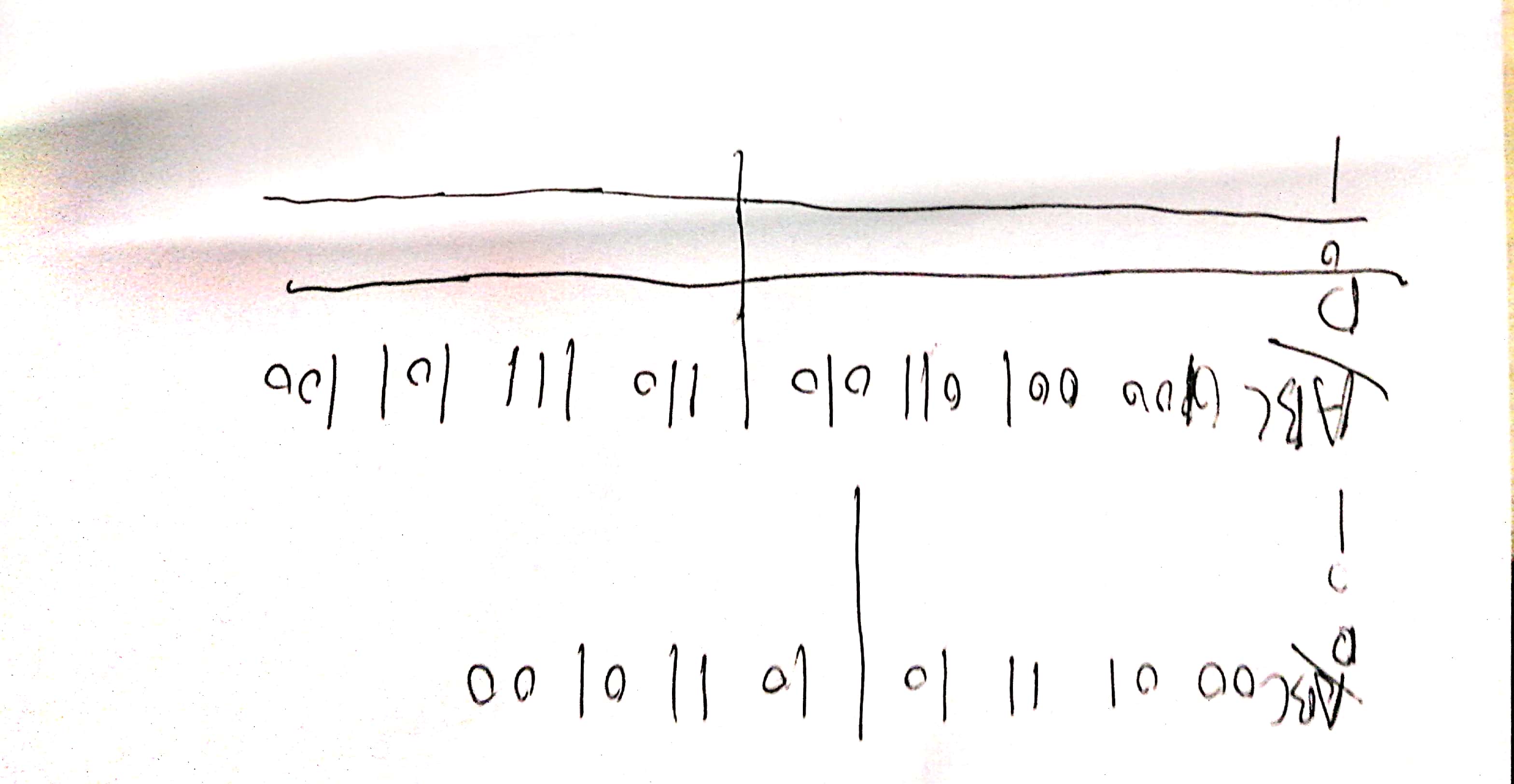
00 01 11 10 (对称轴) 10 11 01 00
000 001 011 010 (对称轴） 110 111 101 100
首先由对称轴对称分布之后在对称轴左边的添0右边添1
一位的格雷码 0 1
两位的格雷码 0 1 (对称轴） 1 0
00 01 （对称轴） 11 10
在卡诺图中也可以使用对称轴的方式进行扩展。
卡诺图的化简
卡诺图化简的依据是 $PA + P \bar{A} = P$
先看一个例子：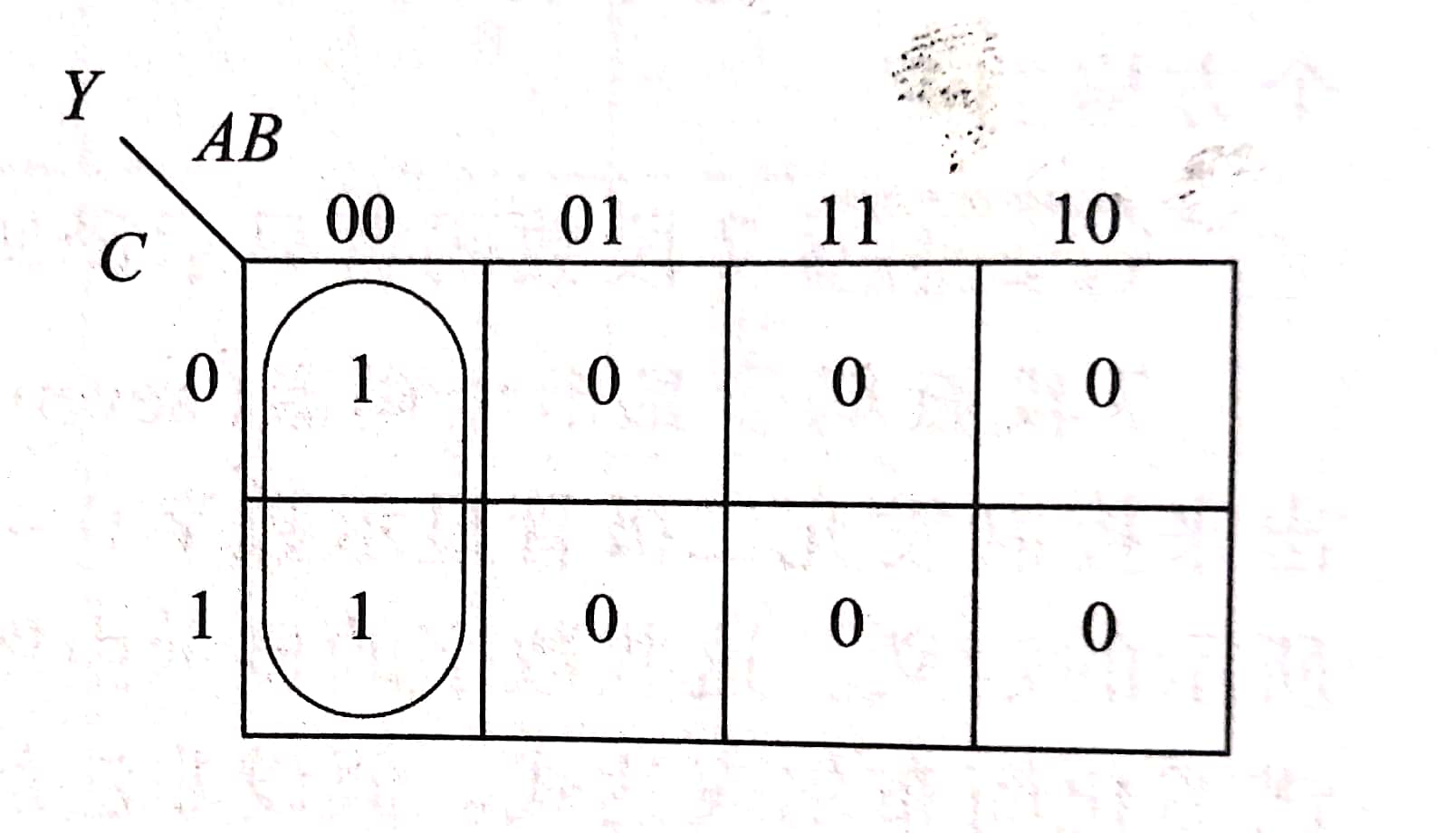
Y = $\bar{A}\bar{B}\bar{C} + \bar{A}\bar{B} C$。可以变成 $\bar{A}\bar{B}(C + \bar{C})$，也就是$\bar{A}\bar{B}$.从卡诺图中可以看出圈中内容正好只有C有变化，便可以通过这个式子将它化简。
- 卡诺图上任何两个标1的方格相邻，可以合为1项，并可消去1个（取值相反的）变量。
- 圈的1的数目必须是2的整数次幂，也就是2,4,8,16…
- 处于对称位置的1可以化简
- 可以重复圈同一个1，因为 A + A = A
- 圈必须覆盖全部的1
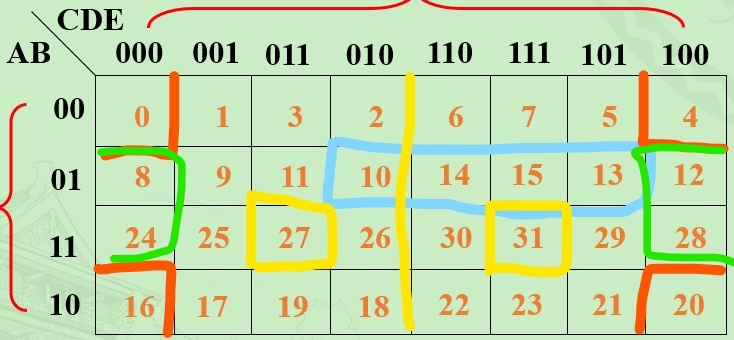
这个图中用线圈起来的部分内部都是1
对于第三点可以举些例子，也就是图中红色标出的四个部分是可以化简的，化简结果为$\bar{B}\bar{D}\bar{E}$.图中绿色部分也是可以化简的。
图中黄色部分也是可以化简的，可以看到他们只有C所在的位发生了变化。他们关于中间黄色的对称轴对称。
联想格雷码的构造过程，对称位置是直接复制并且最高位一个加1,一个加0，所以只会有最高位不同。
但是蓝色部分虽然四个1连在一起，但是通过计算发现他们无法化到最简.结果为$\bar{A}B (D\bar{E} + CE)$
通过上面几个例子可以发现即使是连在一起的1也不一定可以化到最简，通过对称轴折叠可以折叠到一起的才能化到最简
一些概念：
- 卡诺图上的每一个圈都代表一个蕴含项
- 主蕴含项：扩展到最大的蕴含项
- 奇异“1”单元：卡诺图中仅能被单一主蕴含项覆盖的方格
- 质主蕴含项：包含着一或多个的奇异“1”单元的主蕴含项
例如：
图中红色圈出来的1没有对称也没有相邻因此只能自己为一个蕴含项。
图中绿色字和红色字可以组成一个蕴含项，并且除了绿色和红色之外的其他1中只能和红色1组成蕴含项，不能和绿色1组成蕴涵项，因此绿色字是一个奇异“1”单元.
结果为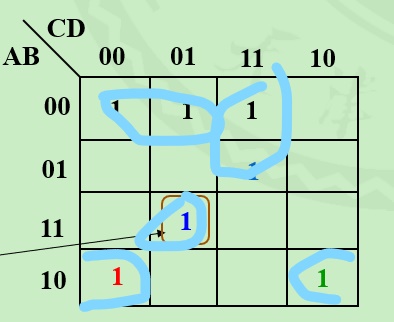
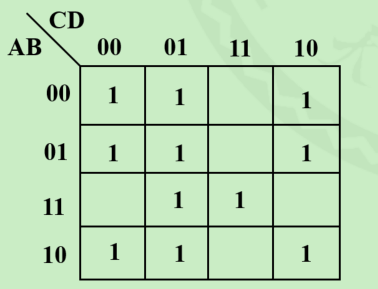
首先找质主蕴含项：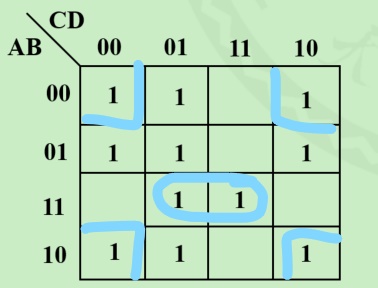 
之后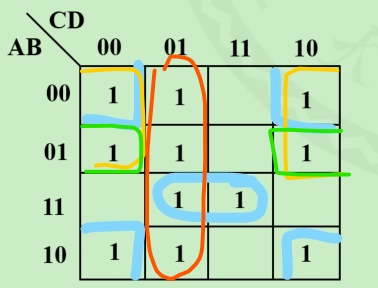
红色部分不必多说，关键是黄色和绿色部分，显然选择黄色的部分，所以要尽可能的选择大的。
化简标准：
- 项数最少，意味着卡诺图中圈数最少
- 每项中的变量数最少，意味着卡诺图中的圈尽可能大
组合逻辑模块
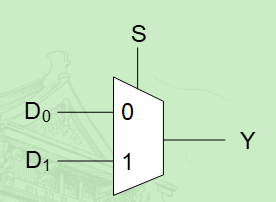
复用器
这是2:1复用器，也就是S为0时，输出由$D{0}$决定，当S为1时，输出由$D{1}$决定。
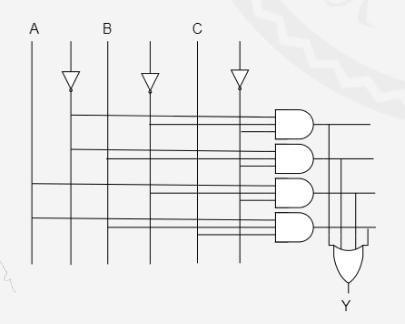
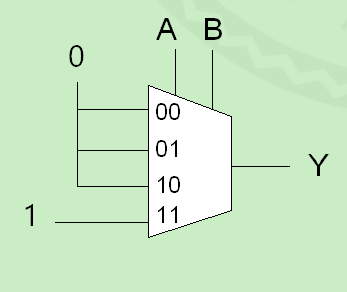
4：1复用器。当A为0，B为0时，输出由$D{0}$决定。A为0，B为1时，输出由$D{1}$决定，依次类推。
还有8:1复用器等，都是通过上方的门控选择哪个输出。
编码器
编码器是用n位二进制代码对 $N=2^n$ 个特定信息进行编码的逻辑电路
EO用来判定是否存在有效输入（即$X_0 , X_1 , X_2 , X_3$都是0时EO=1，其他情况都是0）
如果x0有效并且x1，x2， x3无效则输出00，如果x1有效并且x2，x3无效则输出01…
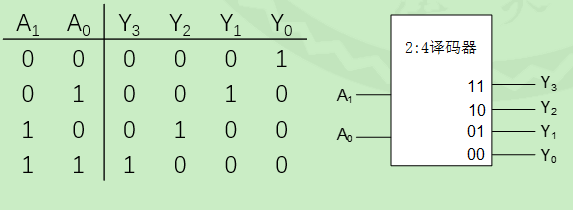
译码器
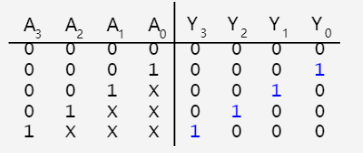
译码是编码的逆过程，输入有n个，输出有$2^n$个
输出时独热的，同一时刻只能输出一个有效信号。相当于每个输出都是一个最小项
毛刺
- 时序： 在实际电路中，某器件从输入到输出是需要经过一定的时间的
- 传播延迟（$t_{pd}$)： 从输入到输出变为最终值所需要的最长时间
- 最小延迟($t_{cd}$): 从输入到输出改变所需要的时间
- 关键路径： 信号传输最慢的一条路径
- 最短路径： 信号传输最快的一条路径
上图A始终为0，C始终为1.它的最长路径就是B通过非门的那一段，最短路径是B直接连到下面的那一段。
假设B由1变0：
- 理想情况下，开始 $\bar{A} \& \bar{B} = 0 \quad \bar{B} \& \bar{C} = 1, Y = 1$ ,在B变为0后，$\bar{A} \& \bar{B} = 1 \quad \bar{B} \& \bar{C} = 0, Y = 1$。结果应该还是1
- 实际上B通过非门的那一条路比直接往下走这个条路慢，因此下面的与门会先输出，并且输出为0，这样Y就会有一段时间输出为0.最后上面的与门也完成输出后Y的结果才会变成1.因此Y的变化为1->0->1
上面的这种现象就被称为毛刺，由于这种现象，所以我们不得不花一些时间等待电路稳定，减少毛刺就可以增快传递速度。
消除毛刺：
- 当两个主蕴涵项相邻时它的相邻边缘会产生毛刺。
例如上图，浅蓝色是最开始画的，而在001和011之间就是两个主蕴含项的边缘了，我们使用额外增加一项来消除边缘