B/B+树

本文最后更新于 2024年10月1日 上午

缘起

B树属于动态查找树，二叉树，平衡二叉树，红黑树都是动态查找树。关于查找的基础内容可看。他们的查找效率都可以达到$log_2^n$，其中n是树的深度。

虽然他们的查找效率和遍历相比已经有很大提升了，但是和哈希相比又大大不如。QMap（红黑树为数据结构）在n=10之后效率就比不过QHash(哈希为数据结构)，越到后面差距越大。但是在数据库中却是使用B树作为数据结构。因为数据库除了考虑速度还要考虑空间，而hash对空间要求大。因此日常对空间不敏感的程序尽量使用hash。

前面已经说了，决定查找次数的是树的深度。假如有65535个数据，那么树的深度为16，那么平均查找深度为 (1 + 2 2 + 3 4 + 4 8 + 5 16 + …. + 16 * 32768) / 65535 = 14.如果14个数据块位于2个不同的磁盘块上（因为是指针不是连续存储），那么就需要2次磁盘读取，所需时间便在毫秒以上。他和直接查找也显现不出太多优势。

因此减少树高就是非常必要的了。一种解决思路就是由二叉树变为多叉树，每一层容纳的数量变多了，树高自然就减少了。此外，各个分支如果树高大致相同毫无疑问平均查找次数是最少的，这就是平衡二叉树的思想。而如果将这两种思路结合就形成了多路平衡查找树也就是B树。

B树

结构

一颗m阶的B树定义如下：

  1. 每个节点最多有m-1个关键字（有m个子节点）
  2. 根节点最少有一个关键字
  3. 非根节点至少有ceil(m/2) - 1个关键字
  4. 所有比当前节点小的节点都在左子树，比当前节点大的节点都在右子树
  5. 所有的叶子节点都在同一层，也就是说他们的深度都相同（保证是平衡二叉树）

例如: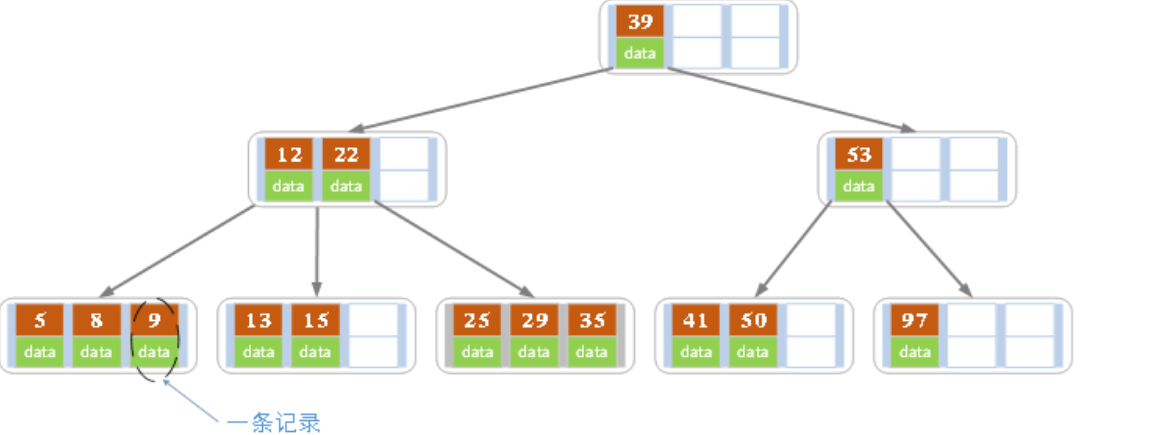

这是一个四阶的二叉树，它最多可以容纳三个关键字但是最多可以有四个子树。为了保证效率在实际应用中阶数一般都大于100.它是将(key, value)作为一个整体看待的，key作为索引，value保存值。例如map[39] = "hello", 39是键，hello是值。

插入

步骤：

  1. 找到插入位置并插入
  2. 判断插入节点的关键字数目是否大于m-1，如果大于则进行第3步
  3. 将节点中间的key放到父节点中，然后将这个节点一分为2，左半边是新插入的key的左子树，右半边是右子树。然后在父节点进行第3步直到停止分裂。

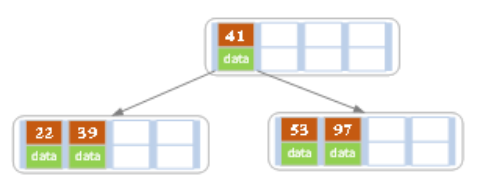
当前是是最多是4个关键字，然后插入插入一个边需要分裂，将中间的41往上提，并且将左半边和右半边作为这个节点左子节点和右子节点。

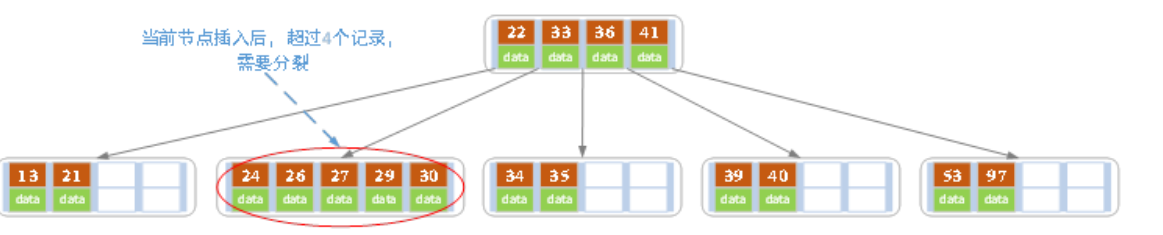
之后插入一个节点后，又需要分裂，但是这次将27往上提发现父节点也装不下了，将子节点分裂完成后父节点也会进行分裂。

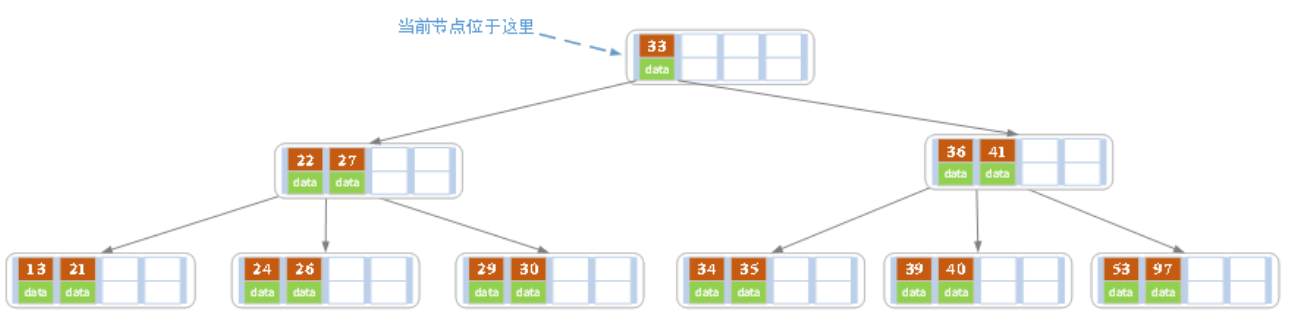
删除

步骤：

  1. 如果位于非叶子节点，则首先使用后继节点替代他（也就是右子树中最小的节点）
  2. 如果右子树节点数量大于m/2-1,则停止，否则进行第3步
  3. 如果左子树节点数量大于m/2-1,则将左子树中最大的往上提，将父节点往右子树中放， 停止。否则将父节点和它的子节点进行合并（左子树m/2-1，右子树不足m/2-1,父节点1合起来不超过m-1，成立)。然后再在父节点中进行第2步。

听起来比较复杂，其实就是将从左右子树中找一个来代替被删除的节点，如果左子树不能就换右子树，如果两个都不能那么降级合并。

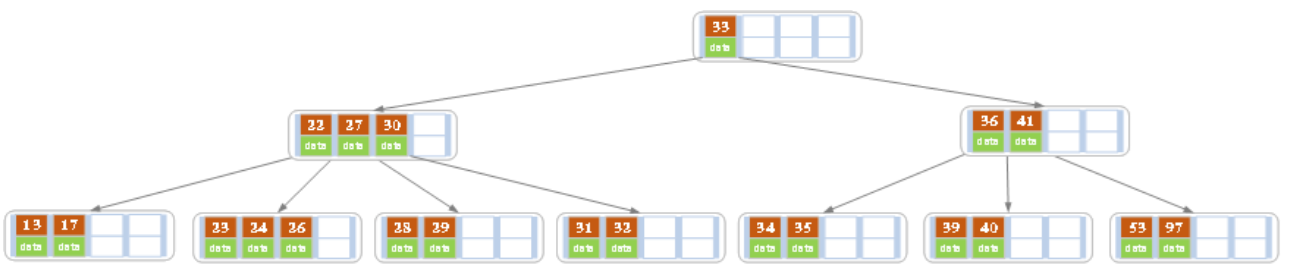
删除27,将28往上提

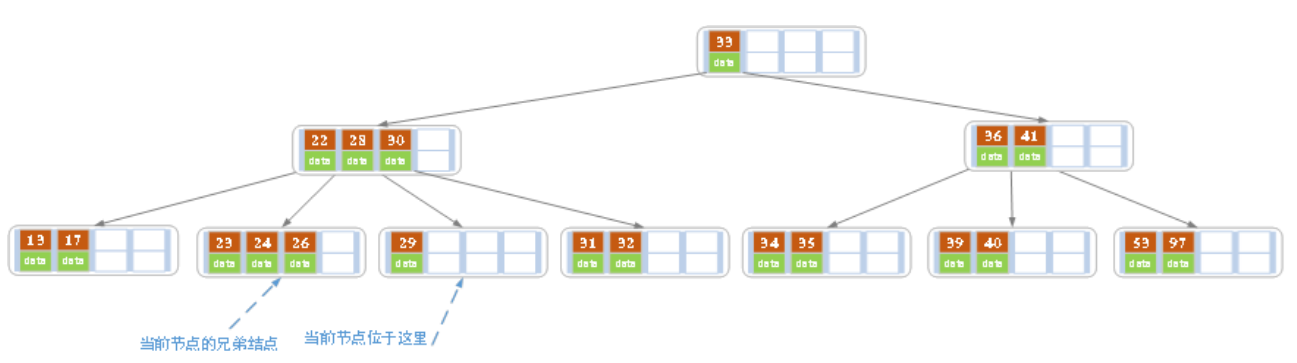
右子树小于ceil(5/2)-1=2,而左子树有三个还可以抽调，因此把26往上，28放到右子树，结束。

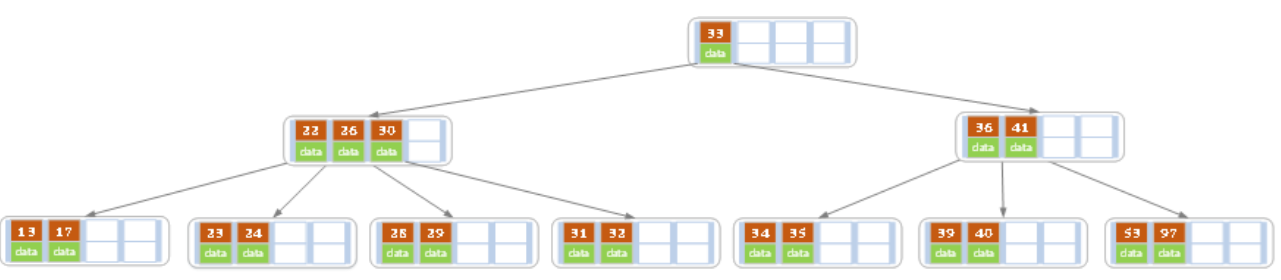
然后再删除32，变成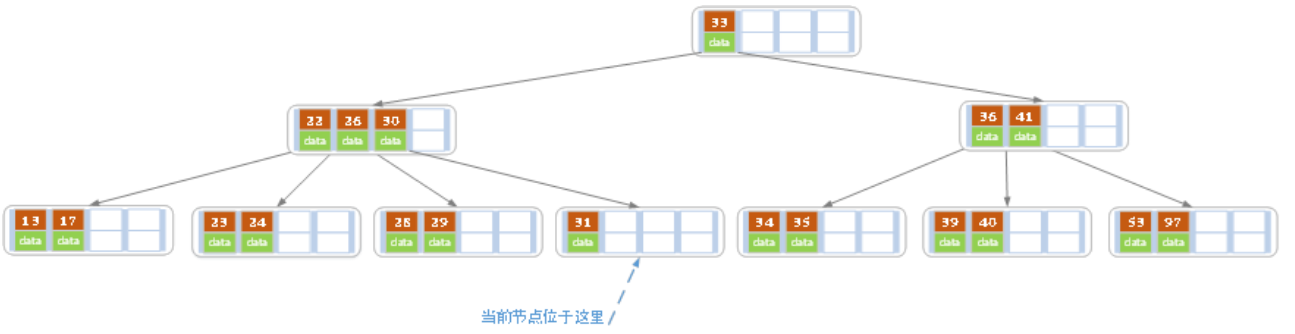

这时右子树不够了，然后左子树也不能再往上提，因此进行合并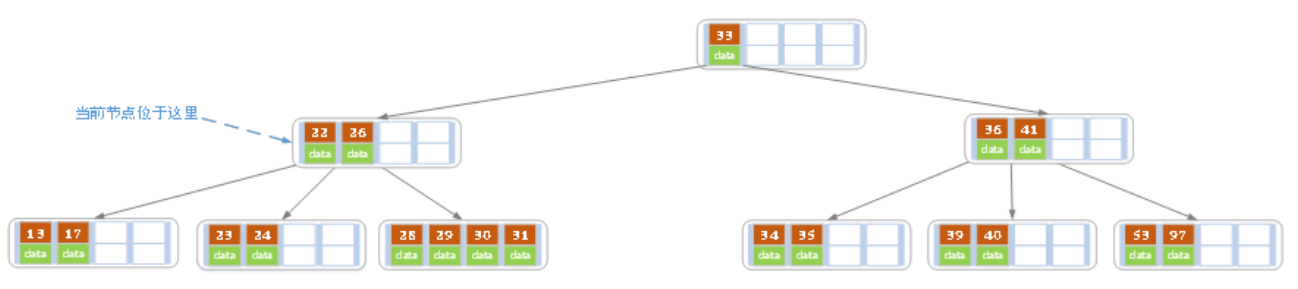

然后审查父亲，发现有两个，满足条件，因此结束。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
#include<iostream>
#include<cmath>
#define TREE_SUM 5
#define HALF_SUM (TREE_SUM % 2 == 0) ? TREE_SUM / 2 -1 : TREE_SUM / 2;
using namespace std;


struct data_type
{
    int key;
    int value;
};
struct node
{
    node* parent;
    node* children[TREE_SUM+1];
    data_type data[TREE_SUM];
    int len;
    int parent_loc;
    node()
    {
        parent = NULL;
        for(int i=0; i<TREE_SUM-1; i++)
        {
            data[i].key = 0;
            data[i].value = 0;
            children[i] = NULL;
        }
        children[TREE_SUM-1] = NULL;
        len = 0;
        parent_loc = 0;
    }
};

int find(int key, node* root, node* ans_node=NULL, bool* success_find=false)
{
    node* temp = root;
    while(temp != NULL)
    {
        bool success = false;
        for(int i=0; i<temp.len; i++)
        {
            if(temp.data[i].key == key)
            {
                ans_node = temp;
                *success_find = true;
                return i;
            }
            else if(temp.data[i].key > key)
            {
                if(temp.children[i] != NULL)
                {
                    temp = temp.children[i];
                    success = true;
                    break;
                }
                else
                {
                    ans_node = temp;
                    return i;
                }
            }
        }
        if(!success)
        {
            node = temp;
            return temp.len;
        }
    }
    return -1;
}

void insert(data_type data, node* root)
{
    node* insert_node;
    int loc = find(data.key, root, insert_node);
    for(int i=insert_node.len-1; i>=loc; i--)
    {
        insert_node.data[i+1] = insert_node.data[i];
    }
    for(int i=insert_node.len; i>loc; i--)
    {
        insert_node.children[i+1] = insert_node.chilren[i];
        insert_node.children[i+1].parent_loc = i+1;
        //还要先判断hildren[i+1]是否是NULL，下面也一样，为了方便查看而省去
    }
    insert_node.data[loc] = data;
    insert_node.children[loc+1] = NULL;
    insert_node.len++;
    while(insert_node.len >= TREE_SUM)
    {
        if(insert_node.parent == NULL)
        {
            node* node1 = new node();
            node* node2 = new node();
            for(int i=0; i<insert_node.len/2; i++)//左子树
            {
                node1.children[i] = insert_node.children[i];
                node1.data[i] = insert_node.data[i];
            }
            node1.data[insert_node.len/2] = insert_node.data[insert_node.len/2];
            node1.parent = insert_node;
            node1.len = insert_node.len/2;
            node1.parent_loc = 0;

            for(int i=insert_node.len/2+1; i<insert_node.len; i++)//右子树
            {
                node2.children[i-insert_node.len/2-1] = insert_node.children[i];
                node2.children.parent_loc = i - insert_node.len/2-1;
                node2.data[i-insert_node.len/2-1] = insert_node.data[i];
            }
            node2.parent = insert_node;
            node2.len = insert_node.len - insert_node.len/2 - 1;
            node2.parent_loc = 1;

            insert_node.len = 1;//根
            insert_node.data[0] = insert_node.data[insert_node.len/2];
            insert_node.children[0] = node1;
            insert_node.children[1] = node2;
            break;
        }
        else
        {
            node* new_node = new node();
            node* parent = insert_node.parent;
            for(int i=parent.len-1; i>=insert_node.parent_loc; i--)
            {
                parent.data[i+1] = parent.data[i];
            }
            for(int i=parent.len; i>insert_node.parent_loc; i--)
            {
                parent.children[i+1] = parent.children[i];
                parent.children[i+1].parent_loc = i+1;
            }
            parent.data[insert_node.parent_loc] = insert_node.data[insert_node.len/2];
            parent.children[insert_node.parent_loc+1] = new_node;

            for(int i=insert_node.len/2+1; i<insert_node.len; i++)
            {
                new_node.data[i-insert_node.len/2-1] = insert_node.data[i];
                new_node.children[i-insert_node.len/2-1] = insert_node.children[i];
                new_node.children.parent_loc = i - insert_node.len/2 - 1;
            }
            new_node.len = insert_node.len - insert_node.len/2 - 1;
            new_node.children[new_node.len] = insert_node.children[insert_node.len];
            new_node.children[new_node.len].parent_loc = new_node.len;
            new_node.parent = insert_node.parent;
            new_node.parent_loc = insert_node.parent_loc + 1;
            parent.len++;
            insert_node = parent;
        }
    }
}

void remove(int key, node* root)
{
    bool success = false;
    node* remove_node;
    int loc = find(key, root, remove_node, &success);
    if(!success)
    {
        return;
    }
    node* now_node = remove_node.children[loc+1];
    while(now_node != NULL)
    {
        if(now_node.children[0] == NULL)
        {
            break;
        }
        now_node = now_node.children[0];
    }
    if(now_node == NULL)//右子树为空
    {
        now_node = remove_node.children[loc];
        while(now_node != NULL)
        {
            if(now_node.children[0] == NULL)
            {
                break;
            }
            now_node = now_node.children[0];
        }
        if(now_node == NULL)//叶子节点
        {
            now_node = remove_node;
            //删除loc位置的节点并重新调整关系
        }
        else
        {
            remove_node.data[loc] = now_node.data[now_node.len-1];
            //调整now_node的关系
        }
    }
    else
    {
        remove_node.data[loc] = now_node.data[0];
        //调整关系
    }
    while(now_node.len < HALF_SUM)
    {
        if(now_node.parent_loc != 0)
        {
            if(now_node.parent.children[now_node.parent_loc-1].len > HALF_SUM)//左子树可以提供,先要判断左子树是否为空
            {
                //将左子树最大的节往上提，父节点往下
                break;
            }
        }
        if(now_node.parent_loc != now_node.parent.len+1)
        {
            if(now_node.parent.children[now_node.parent_loc+1].len > HALF_SUM)
            {
                //和上面类似
                break;
            }
        }
        //两边子树都无法提供，进行合成并转到父节点
    }
}

B+树

B+树基本结构和B树相同，并且有所延伸

  1. B+树分为内部节点（索引节点）和叶子节点，内部节点只负责索引，不保存数据，由叶子节点保存数据
  2. 每个叶子节点都有指向相邻叶子节点的指针（链表），并且从小到大排列

插入

  1. 根据key找到插入位置，如果插入后<=m-1,则结束。否则分裂节点。前m/2变为左子树，第m/2+1个节点的key（在子树中节点还存在）拉到父节点中，然后把m/2+1到m-1的节点的作为右子树。当前节点到父节点进行第2步
  2. 对于索引类节点，进行分裂时作为父节点的节点不在子树中保留，和B树类似

B+树插入和B树最大的不同是在叶子节点的数据是不会删除的，这样带来一个好处是遍历速度明显加快，假如保存每个叶子节点所拥有的数据可以直接达到类似于索引的效果。缺点是会有一些相同的记录，带来了空间上的浪费。

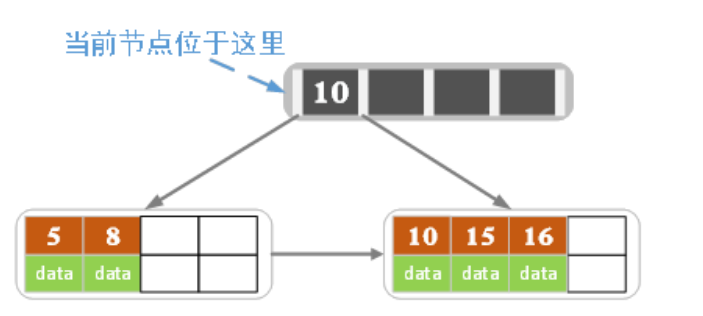
假设这是初始情况，现在插入16.中间节点是10，将10作为索引放入父节点中。m为5，m/2=2。因此左子树有2个元素，右子树有三个。

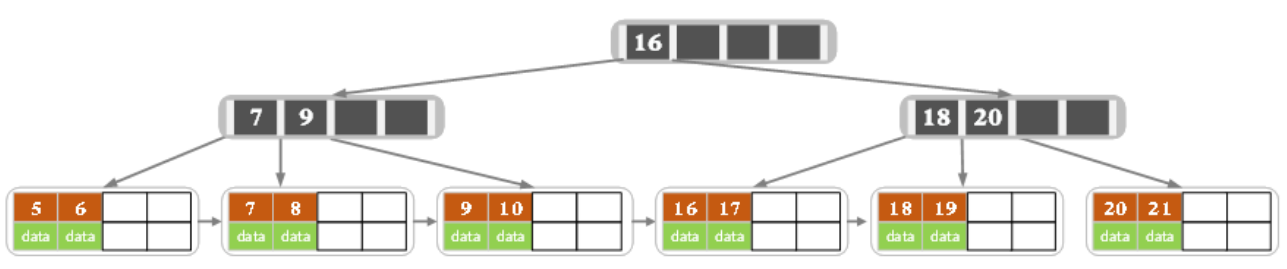
删除

  1. 删除叶子节点中的key，如果大于ceil(m)/2 - 1，则删除结束，否则进行第二步
  2. 如果兄弟节点有富余，向兄弟节点借（拿）一个记录，并且他们的父节点变成拿的那个节点。如果没有富余到第3步
  3. 进行合并，删除索引节点并且左右子树合并成一个。然后检查索引节点是否满足要求，之后和B树相同。

问： 如果删除的节点正好是索引节点有关系吗？

因为索引节点正常情况下是右子树中最小的那个，删除之后左子树还是都比父节点小，右子树比父节点大，并没有破坏关系，可以正常插入删除，因此没有影响。

现在删除7，因为左子树正好是m/2-1，因此只能合并，删除7的索引合并节点变成

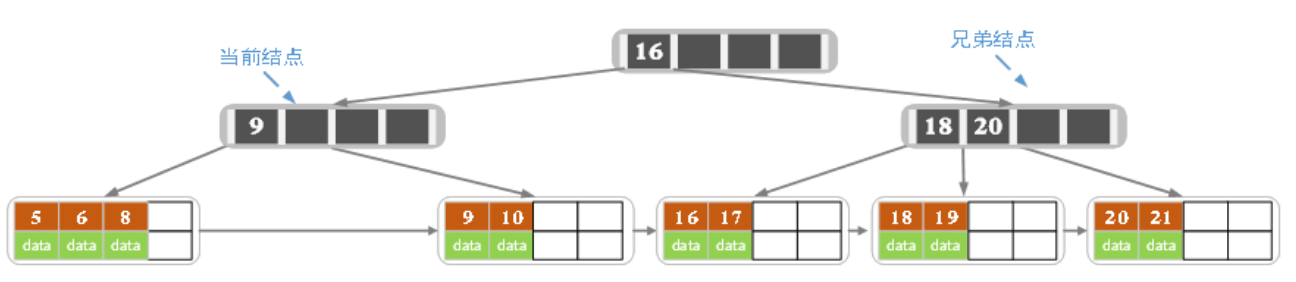
之后合并索引节点变成

参考

B树和B+树的插入、删除图文详解

数据结构
B/B+树
https://www.xinhecuican.tech/post/69629cf2.html
作者
星河璀璨
发布于
2021年7月26日
许可协议