压缩矩阵

对于特殊的矩阵，例如上下三角矩阵，对称矩阵，三对角矩阵，可以转化成1维矩阵，减小空间的消耗。

特殊矩阵

对称矩阵

对称矩阵有 aij=aji的特性，因此可以只保存一边，也就是压缩成 n(n+1)/2个

如果我们用一个一维数组s[n(n+1)/2]来保存，那么它域原矩阵的对应关系

k= i(i-1)/2+j-1 i>=j
    j(j-1)/2+i-1  i<j

这个式子先只考虑一边，先看i>=j的情况。此时第一行中压缩矩阵只保存一个值，第二行两个值，依此类推。所以对于第i行先把前i-1行中对应压缩矩阵的值的数量加起来，也就死i(i-1)/2，之后再加上第j行的第j-1个（这里因为数组下标是从0开始）。

这个例子中的行数是从第一行开始，实际上应该从第0行开始，所以

k= i(i+1)/2+j i>=j
  j(j+1)/2+i i<j

上下三角矩阵

对称矩阵行数和列数相同

上三角矩阵其实就是对称矩阵中 i>=j的那一段

下三角矩阵中第一行的压缩矩阵元素数量是n,第二行是n-1,以此类推，我们也可以得到相应的关系式

k=（2*n-i-1)*i/2+j i<=j
  (2*n-j-1)*j/2+i i>j

三对角矩阵

除了第一行和最后一行有两个元素之外，其他行都有三个元素

对于a[i][j]来说，前面有 3i-1个元素，本行它前面有j-i+1个位置。所以k=2 i+j

反之，如果在压缩矩阵中是第k个位置，那么在原矩阵中 i=(k+1)/3 j=k-2*i

稀疏矩阵

对于非零元素较少的矩阵，可以直接用一个结构体保存 i,j ,sum，然后再用一个结构体数组来保存所有的值。这个数组是从左至右扫描遍历的。一般稀疏矩阵中元素只占5%

稀疏矩阵转置的算法

首先，如果用朴素的算法，就是从第零行开始遍历每一列，然后把列变成行。

如果我们用两个数组分别保存 每一列中元素的数量以及每一列在新的稀疏矩阵中的位置，就有办法可以加快速度

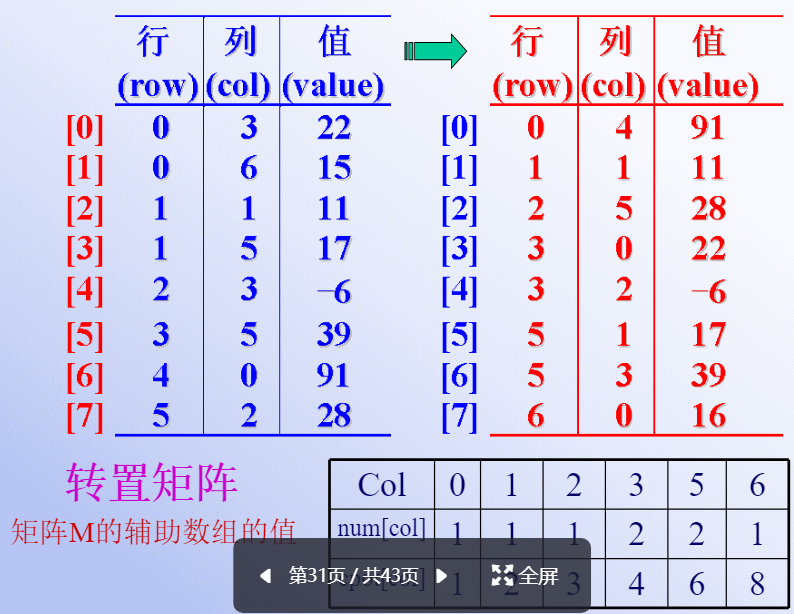
例如：

cpot 第一个位置是一是因为数组下标从1开始

for循环中注意q=cpot[col]，代表现在这个位置已经有东西了，所以再最后++cpot[col]代表现在这一列在新稀疏矩阵的首位置要后移一位。

其次，因为转置前行号已经是从小到大排了，所以行号小的一定在前面。