AOV网络

aov网络指的是用顶点表示活动的网络。讲个例子吧

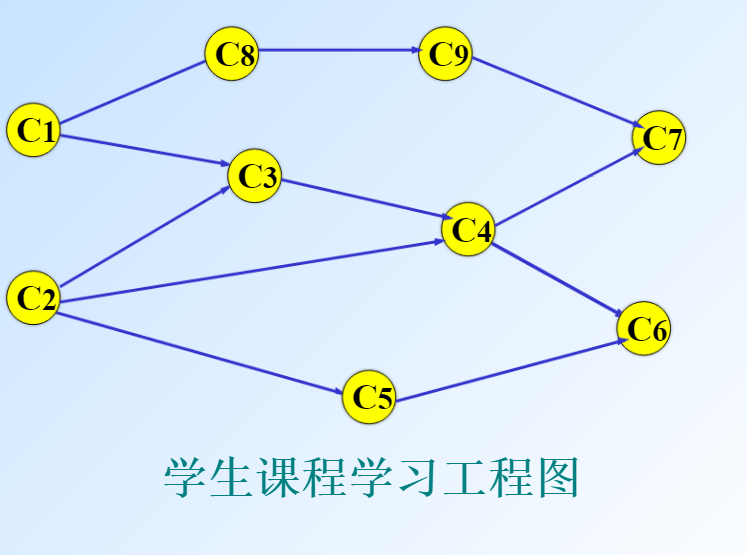
例如学习课程有个前后顺序，前面一门课没有学完后面一门课动不了手。这样就可以用顶点表示课程，然后用有向箭头表示学习的次序，这样就是一种AOV网络。并且显然每个点都要走，因为每门课都要学。

后面这个数字代表先修课程

检测有向环可以用对AOV网络构造拓扑序列。构造方法等会讲，如果有环，那么就会出现永远都有入度的情况，就说明有环。

构造过程

就拿上面一个图来说吧。必须先要学完c1，c2才可以学c3.学了c1又可以学c8，按照这样的顺序就可以得出学习顺序是C1C2C3C5C4C8C9C7C6。当然，还有许多其他的次序。

从中我们可以发现一个规律，假如每当我们学一门课就删去这些边，那么我们可以学习一个课程时入度一定为0.例如我们学完1和2后3入度就是0所以现在我们可以学了。如果入度不为0说明我们还有前置知识我们没有掌握，就不能学。

总结：找出入度为0的点，删去与之相邻的边，然后找新的入度为0的点，重复上述过程。

下面给出模板：

#include<iostream>
using namespace std;
struct edge
{
    int val;//边权
    int last;
    edge* next;
};
struct node
{
    int insum;//入度
    edge* first;
};
node nod[100];//随便设的数字，也可以new来构建
void init()
{
    for(int i=0; i<100; i++)
    {
        nod[i].first = NULL;
        nod[i].insum = 0;
    }
}
void addedge(int sum, int first, int last)
{
    //用后插法
    edge* temp = new edge;//needfree
    temp->val = sum;
    temp->last = last;
    temp->next = nod[first].first;
    nod[first].first = temp;
    nod[last].insum++;
}
int main()
{
    int sum, first, last;
    node* tempnode;
    while(cin>>sum>>first>>last)
    {
        addedge(sum, first, last);
    }
    node* aovstack = new node;//needfree,链栈，用来存放入度为0的节点
    int time = 0;//记录栈中有多少元素
    for(int i=0; i<100; i++)
    {
        if(nod[i].insum == 0)
        {
            tempnode = nod[i];
            tempnode->first = aovstack->first;
            aovstack->first = tempnode;
            time++;
        }
    }
    while(time > 0)
    {
        time--;
        tempnode = aovstack->first;
        node* temp = aovstack;
        aovstack = aovstack->first;
        delete temp;
        edge* tempedge = tempnode->first;
        while(tempedge != NULL)
        {
            if(--nod[tempedge->last].insum == 0)
            {
                time++;
                tempnode = nod[tempedge->last];
                tempnode->first = aovstack->first;
                aovstack->first = tempnode;
            }
            /******************
            *output...
            ***************/
            
        }
    }
    /***************
    * delete...
    *******/
}

AOE网络

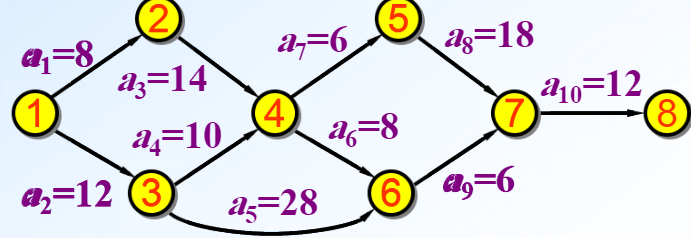
这个是用边表示活动，顶点表示事件。

这是一个AOE网络图，注意和上面类似这里每一条边都是要到的。我们要找的就是花费时间最长的那条路，因为那条路走完了所有活动才完成。那么这条路叫做关键路径，这条路径上的活动叫做关键活动。如果我们想缩短工期的时间，那么我们就要先缩短关键活动的时间。

几个名词

事件最早可能开始时间 ve(i)

事件最迟允许开始时间 vl(i)

活动最早可能开始时间 e[i]

活动最迟开始时间 l[i]

所以关键活动就是 e[i] == l[i] ，因为最早时间和最晚时间相同说明耽误不得。

求法

代码比较简单，这里只讲一下思路。

同样使用邻接表。用四个数组分别表示上面四个名词。首先求前面两个。

事件最早时间这么多到那个点的路径中最晚的那个。例如上面的6点应该是40而不是30，因为只有最晚的那个完成了才能算真正到了那个点。

事件最晚开始时间要从后往前算。最后那个点的最晚开始时间我们一般是知道的，就是截至时间。然后往前面去减，如果有多条路径到那个点就选最小的。同样的道理因为所有边走完这件事才算做完了，如果你选大的相当于到最后那个点的所需时间少，结果这边走完了那个时间小的还没有走完。

举个例子：假设8点的截至时间是60，那么4点的截至时间应该是从8到7到5那一条。

活动最早开始时间是活动的起点的最早开始时间

活动的最晚开始时间是活动的终点的最晚开始时间减去这条边的权

从这个代码中我们看出每个顶点遍历就可以了。

最大流问题

引例： 为了应对环境变化，人们在月球上建立了新的基地。2077年，由于未知原因，环境发生了连环崩溃，现要紧急将人们迁往月球。

初始所有人都在地球上，有若干太空站作为中转，试设计一个算法，让所有人都能尽快逃离。

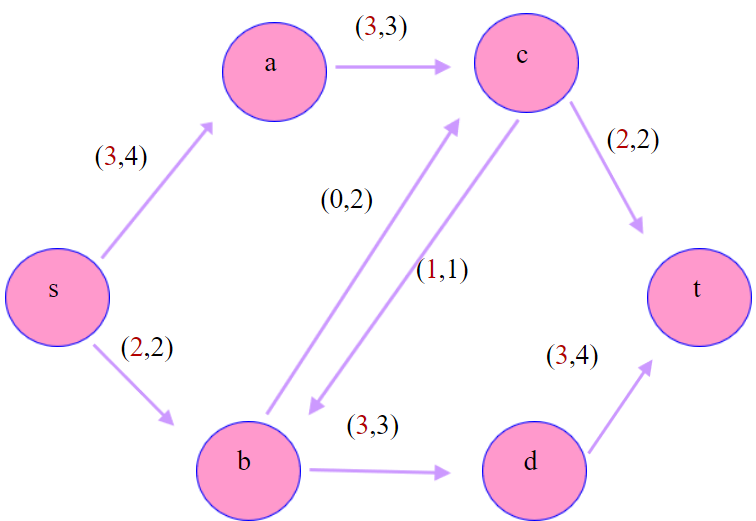
如图，s是地球，t是月球，中间的节点是空间站。每个括号的右边代表最大的输送速率，而左边表示现在的输送速率。

现在我们需要寻找一种方法使得输送到月球的速率最大。

一些符号及定义

V表示顶点集合
E表示边的集合
s表示网络的源点，t表示网络的汇点
对于每一条边(u, v)， 有容量c(u, v)
如果c(u, v) = 0 表示u，v之间不存在边， c(u, v) > 0，表示(u, v)之间右边
对于每一条边，都有实际流量f(u, v)

网络流的三个性质

  • 容量限制： f(u, v) <= c(u, v)
  • 反对称性： f(u, v) = -f(v, u)。这一条只是认为规定，为了方便计算。也就是从a到b是正的，从b到a就是负的
  • 流量平衡： 任何不适源点也不是汇点的节点，流入的流量和等于流出的流量和。即对于任何节点v，有$\sum_{u \in V} f(v, u) = 0$

只有满足上述三个性质，就可以称为一个合法的网络流，也叫可行流。零流一定是可行流

弧的分类

  • 零流弧： f(u, v) = 0
  • 非零流弧
  • 饱和弧
  • 非饱和弧
  • 前向弧： 弧的方向和路的方向一致（弧方向和这条边的箭头反向一致）
  • 反向弧： 弧的方向和路的方向相反
  • 残量网络： 定义残量 r(u, v) = c(u, v) - f(u, v).也就是一条弧还可以有多少流量经过

左边是网络流，右边是残量网络

对于有流量的边，他们在残量网络中是和原来的方向相反的，称为可减流量

我们需要做的就是寻找一条虫原点到汇点的路，并且找这条路上的最小值。然后减去最小值重新构建残量网络。不断重复这个过程知道找不到从源点到汇点的路。

我们可以这样做是因为对于图中非源点和汇点的节点，我们一定会穿过然后穿出，因此它的总流量没有变化，没有破坏性质。而对于源点，因为是从源点出发，所以从源点流出的量一定增大，因此通过这种方法流出量会不断增大。

标号法寻求可改进路（Ford-Fulkerson算法）

标号法和上面说的算法其实类似。算法过程为：

标号形式为： （$V_x$, $L(V_x )$),其中$V_x$表示$V_i$的标号是从哪里得到。

  • 如果$V_x$前为+号，表示有一条有向边（$V_x$, $V_i$)且该有向边的流量不满，
  • 如果为-号，表示有一条有向边($V_i$, $V_x$)且这条边有流量
  1. 首先给$V_s$标上(0, $\infty$)
  2. 从V_s开始，取一个和它相邻的边，如果是从起点到终点并且f(u, v) < c(u, v)，那么给终点进行标号为（$V_i$, L($V_j$))。或者如果这条边是从终点到该点并且f(u, v) > 0标号为(-$V_i$, f(u, v))。
  3. 从标号的点开始重复进行第二步知道到达终点。
  4. 到达终点后，说明我们就找到了一条可改进路，则进行调整过程

例如：

首先$V_s$标号为(0, $\infty$)

之后寻找可以标号的边，我们发现1可以标号，因为f(u, v) < c(u, v).

然后从1开始寻找，我们发现2可以标号，因为这条边反向并且流量大于0，因此标号为(-$V_1$, 1).

之后都是重复进行这些过程直到到达终点。然后选取这些流量中的最小值进行调整

它的基本思想就是寻找可以流出的点。因为源点的流量是无穷的所以它需要寻找下一个可以流出的点，正向好理解。反向是因为这个过程不会破坏合法流的性质，因为源点流出了，让某一个流入这个节点的流量变小不会影响最终结果，但是他会增大从源点流出的量。

不会破坏性质是因为我们每个节点都在寻找流出。反向的流入减小也可以释放从上一个节点来的流量压力，并且反向流入减小说明反向的那个点流量增大（因为流出减小），所以可以看成从起点流向终点。

最大流最小割定理

一个割集（S, T)的两个点集组成.并且起点和终点分属两个集合。

割集之间的容量是$C(S, T) = \sum_{x \in S} \sum{y \in T} c(x, y)$,即从s到t的所有边的容量之和。

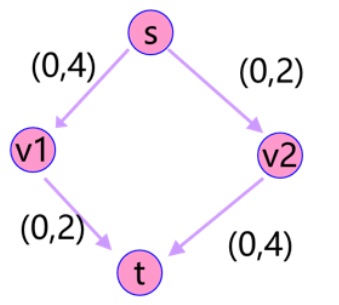
例如上图中s和v1组成一个点集，V2和t组成一个点集，则他们之间的容量为4。如果s单独组成一个点集，其他点组成一个点集，则容量为6。

最大流最小割定理： 任一网络D中从Vs到Vt的最大流的流量等于分离Vs和Vt的割集中容量最小的割集的容量。也就是最大流的流量等于最小割的容量。

意义： 找到了最小割，就可以通过最小割的流量来扩大最大流。

证明：

割集之间的流量： $f(S, T) = \sum_{x \in S} \sum{y \in T} f(x, y)$。他和容量不同，容量只有从S到T的边才算，而这里流入流出割集的边都算。

设X， Y， Z为顶点子集（包含多个顶点）

  • f(X, X) = 0(也就是说一个顶点内部的流量为0）
  • f(X, Y) = -f(Y, X)
  • f(X $\cup$ Y, Z) = f(X, Z) + f(Y, Z)
  • f(X, Y $\cup$ Z) = f(X, Y) + f(X, Z)

定理： 任意不包含s和t的顶点集X，流入流出集合的流量为0.

定理： 整个网络的流量等于任意割的流量

证明：

通过上面的定理我们知道了网络的流量不能超过最小割的容量（因为所有割的容量都要相同）。因此可以得出最大流等于最小割

最小割的求解

残量网络中可以走通的边表示还有可以变化的余地，走不通表示已经满载。在最大流中，所有满载的边就构成了阻止流量继续增加的瓶颈，这些瓶颈共同构成了最小割的边。

于是求解步骤为：

  1. 求最大流
  2. 求最大流的残量网络
  3. 在残量网络中，从源点出发搜寻所有可到达的节点，这些节点构成的集合就是S

二部图的最大匹配

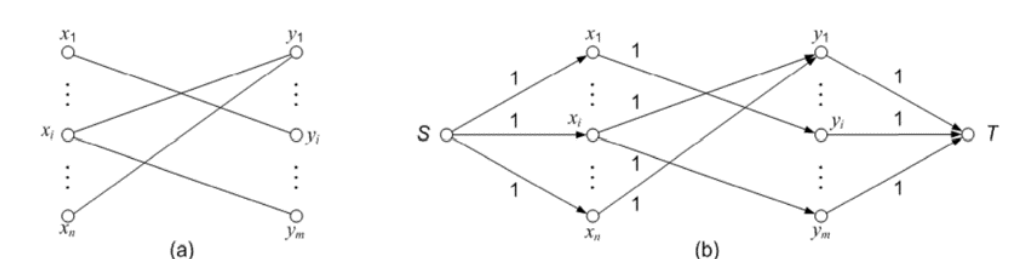
我们可以利用网络流求二部图的最大匹配。二部图是寻找两个点集，使所有边的端点分属两个点集。

左图就是一个二部图。而右边就是增加了源点和终点的扩展图，通过这个扩展图使用最大流算法就可以找出最大匹配。

过程：

  1. 增加一个源点和汇点并且s向x每一个点增加有向弧，y向t增加有向弧
  2. 将x和y间的所有边都改成有向弧，方向是从x到y
  3. 所有有向弧的容量都设成1
  4. 运行最大流算法，x和y之间被选中的边数就是最大匹配数

证明：

  1. 首先证明每个x唯一的匹配一个y
    由于容量都是1，因此每个x不会分出一半流向两个y，每个y也不会接受两个x的流入
  2. 最大流就是最大匹配
    以(S, x1, x2,…)作为一个割集，其他点作为一个割集，也就是说割边就是原来集合中的所有边。而最大流时流量最多，也就是说割边选取的最多。

价值匹配

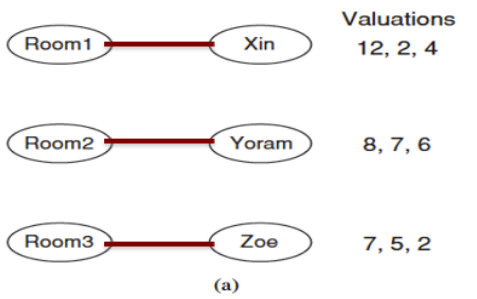
上面讲的匹配是站在全局角度上，只考虑了怎么让匹配数量更多，却没有想过每个个体对这个匹配是否满意。每个人对不同的物体不仅仅是简单的要或者不要，他对不同物体有不同的喜爱程度。

例如上面三个人对三栋房子有不同的偏爱程度，那么我们怎么评价上面的匹配好不好呢？一种方式是总的喜爱程度最大，这个例子中是12+7+2 = 21.

但是这种方式不一定好，因为为了得到最大收益可能让很多人选择他不想要的东西。另一种方法时尽可能公平匹配。

这种匹配问题实际上在生活中经常遇到，例如买房子。当房价提高后没有这么喜欢这个房子的人可能就不会买了，而真正喜欢这个房子的人会出高价去买，这样卖家高兴（因为他卖出了高价），买家也高兴（虽然出了高价但是买到了想要的房子）。当然这只是一个例子，现实生活中还要考虑恶意抬价的可能。

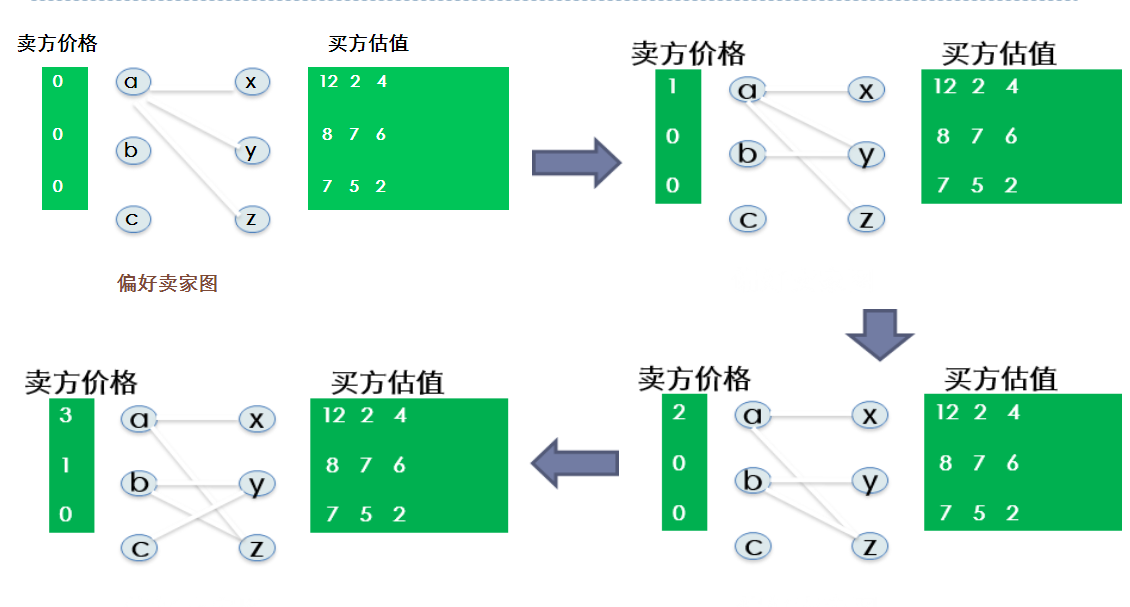
根据上面的自由市场的思想我们可以使用算法进行模拟。

首先买家会选择买方价格-卖方价格最大的那个，如果卖方同时有多个进行选择则涨价。如果没有人选择则降价。直到中间连线可以形成完美匹配（也就是卖方每个点都可以匹配卖方）中止

社会网络中的价值匹配

可以预见，B应该最终会获得多一点，因为他和其他人的联系更多，但是具体多多少，有何判断交易是否稳定。

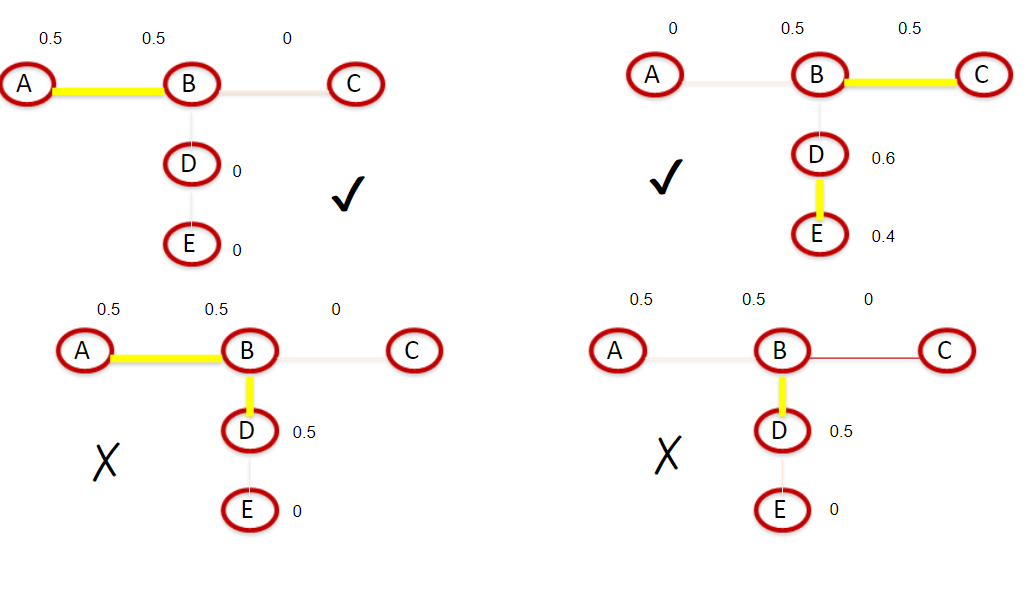
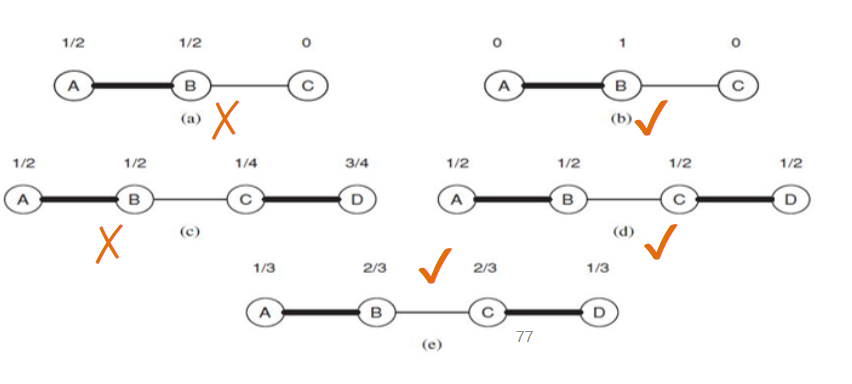
如图，前两个是合法的结果，后两个是不合法的结果，一个合法结果需要满足两个条件

  • 如果u和v成交了，那么他们二者值之和一定是1
  • 如果没有成交值一定是0

但是合法的一定合理吗？例如第一种合法但是A和B的分配会一样吗？

为了进一步解决匹配问题，提出了稳定结果。

稳定结果指的是不存在潜力边，也就是一条边两端的价值之和小于1。出现这样一条边就表示如果让这条边的端点进行匹配可以获得更大的价值。

但是这种情况下还是会有问题，例如图d。中间两个节点应该会获得更多，但是它却和两边的端点获得的一样多。

考虑到节点的度数对节点值的影响，提出了那什议价解。

  • 外部选项： 这是那什考虑到其他节点对价值分配造成影响而提出的。它指的是可以从该节点相邻节点获得的价值。例如

那什议价解条件：

首先假设外部选项分别是x和y

  • x<=1 && y <= 1 && x+y <= 1(因为如果大于1那么两个节点的值不可能优于外部项，也就不可能成交）
  • 那什议价解的组成分为两部分。
    • 从外部选项获得的，假设可以全部获得，也就是x和y
    • 从两个节点连线中获得的，在这条连线中他们是均衡的因此对半分。每个节点可以获得 s = (1 - x - y)/2(因为两个节点先获得了外部的x和y）
    • 也就是说a节点可以获得x + s, b节点可以获得y + s

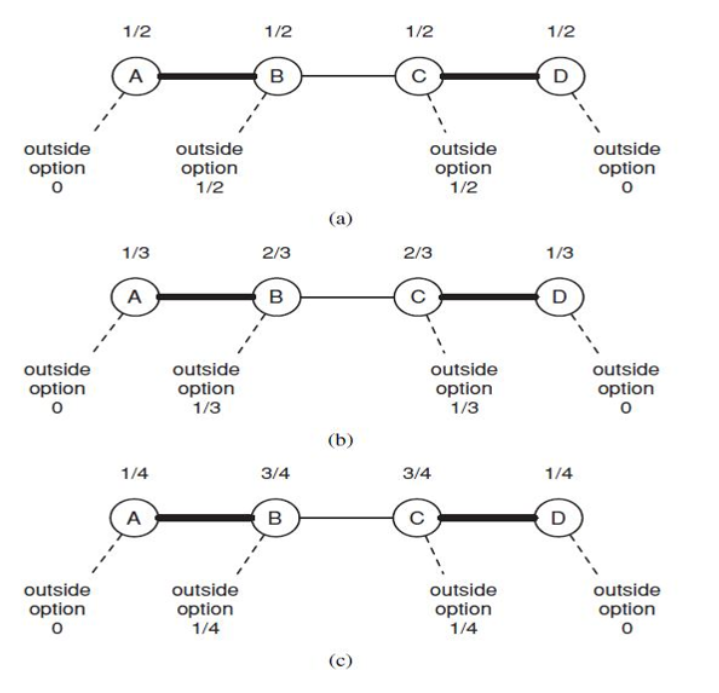
例如图a中a节点想要获得0+(1-1/2)/2 = 1/4,b节点想要获得3/4，和实际并不相等。因此不是均衡结果

而按照那什议价解算出来的结果并不能得到均衡。例如图a经过计算之后会到图3，而图三中a节点想要3/8, b节点想要5/8，和实际还是不相符。

最终实际图b是那什议价解，a想获得(0 + (1 - 1/3)/2) = 1/3, b想获得(1/3 + (1 - 1/3)/2) = 2/3,和实际相符