静态查找

顺序查找

就是一个个找，过程不必多少。

如果查找每个元素概率相等，那么查找第n个元素只需要一次，第n-1需要两次…。所以平均查找次数是 1+2+…+n / n = （n+1)/2

折半查找

其实就是二分查找,代码

分块查找

分块查找就是每个找出每个块中最大的元素然后单独建一个表，之后就可以先查找这个表然后根据表来查找。大致意思就是这样，具体代码

动态查找

二叉排序树（查找树）

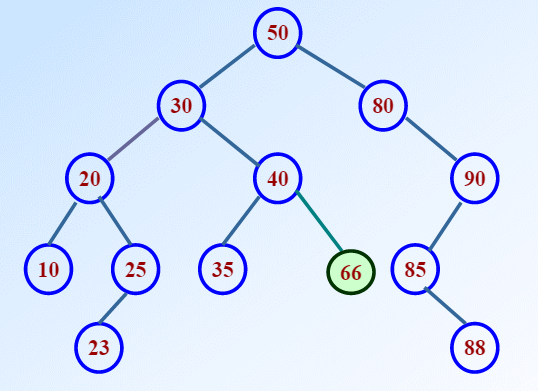
二叉查找树特点是左儿子都比父亲小，右儿子都比父亲大。

上面就不是二叉排序树，因为66比50还要大。

用链表进行存储。

struct node
{
    node *lchild;
    node *rchild;
    int val;
}

二叉树的查找算法：

  1. 如果二叉树是空，那么直接返回
  2. 如果该节点的val正好是要查找的数，则查找成功
  3. 如果大，那么去右边找
  4. 如果小，去坐标找

插入

先要进行查找，如果查找不成功才会插入。

插入过程最好单独写一个函数，因为使用递归。如果要插入的点比当前点大，那么就去右边，反之就去左边。知道这个点是空为止，把要插入的点插入到这个空的点中。

删除

如果要删除的点是叶结点，那么直接把这个点变成空（因为父亲节点的儿子指针就指向这个节点，现在把这个节点变成空，那么儿子指针就指向空）

如果要删除的节点只有左子树或者右子树，那么让父亲对应指针指向那个子树就可以了。所以最好把父亲节点也用一个变量存储。

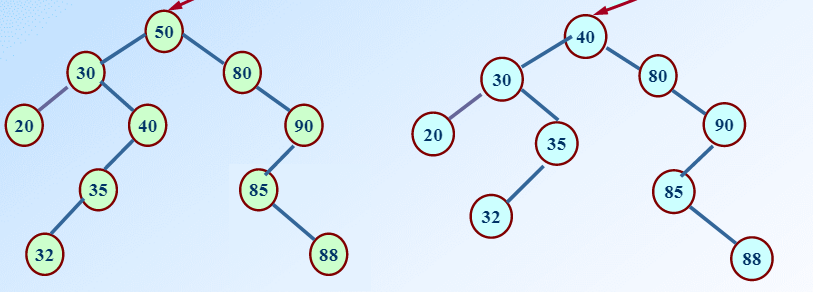
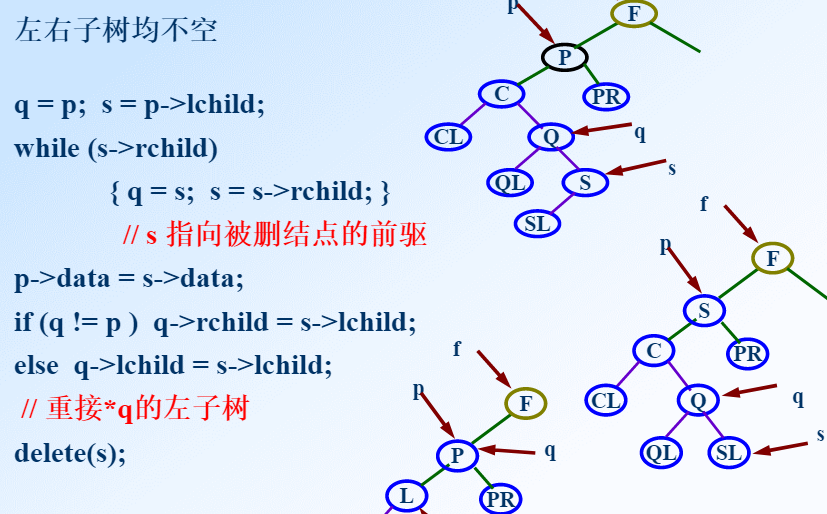
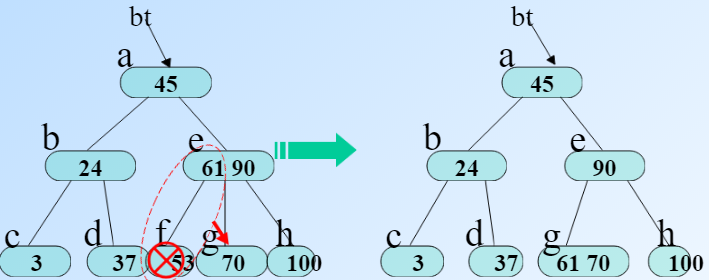
如果要删除的节点左右子树都有，就用它的前驱替代，然后删除前驱。

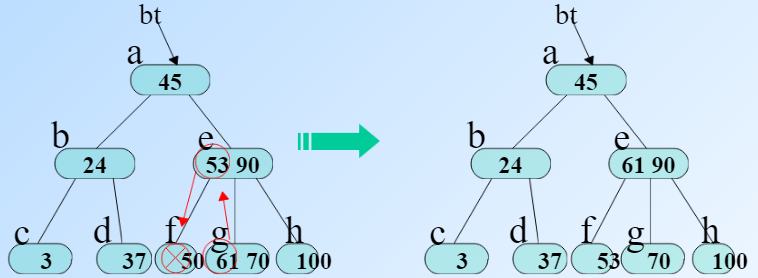
左边是删除前，右边是删除后。

前面一段代码是找前驱，前驱是s，而q是s的父亲，如果p==q说明p的左孩子就是s并且没有没有其他分支

效率 2logn

平衡二叉树

平衡二叉树的特点是左右子树深度之差小于等于1.

构造方法

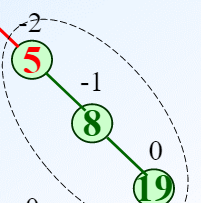
加入一个代表深度差的标记bf，如果左边比右边深为正，右边比左边深为负。例如：

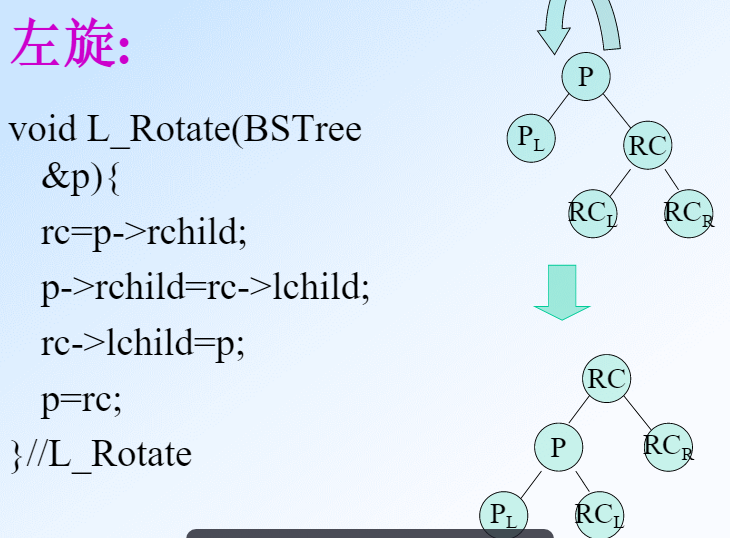
上面的数字就是bf值。这个例子中是失去平衡的右子树的右子树导致的，也就是右右，可以向左旋转。让5做8的左节点，8连接根节点，19连接右节点。

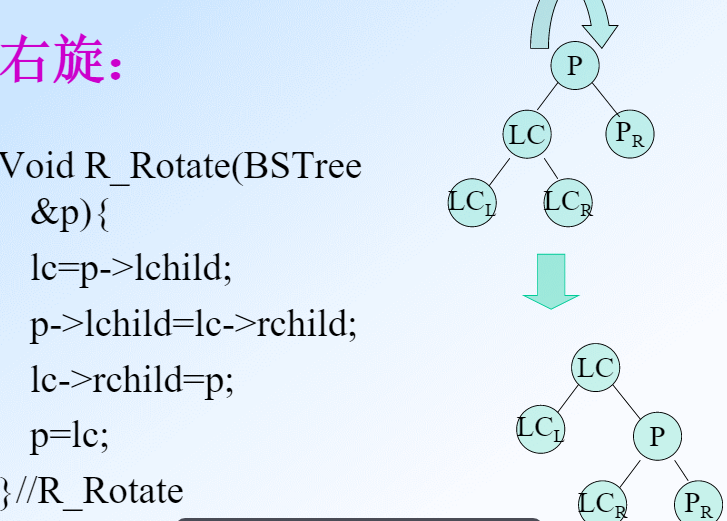
如果是左左，那么向右旋转。

如果是左右，那么先左旋再右旋。

如果是右左，那么先右旋再左旋。

那么现在就知道如果不平衡应该怎么做了。但是插入时怎么判断平不平衡呢？

如果是空树，那么把这个点做根节点。

否则就按照二叉排序树的方法进行插入，插入完成之后又从底部递归。如果最终插入到右边就让父亲-1，如果插入到左边就让父亲加一。如果父亲>=2就找左儿子，如果左儿子是1那么就是左左的情况，那么右旋，反之先左旋再右旋。如果<=-2也是同样的方法。

注意，左旋和右旋是以根节点为基准的。在左左或右右的情况中，根节点是最上面那个点p，右旋就是把p和lc互换。但是在左右和右左的情况中不是这样。

如果是左右的情况，先以第二层的点作为根，右旋就是第二层的点和第三层的点换一下位置，顺便把原来第三层的左儿子挂到原来第二层的右儿子上（因为原来第三层的点变成第二层，右儿子没有了）。

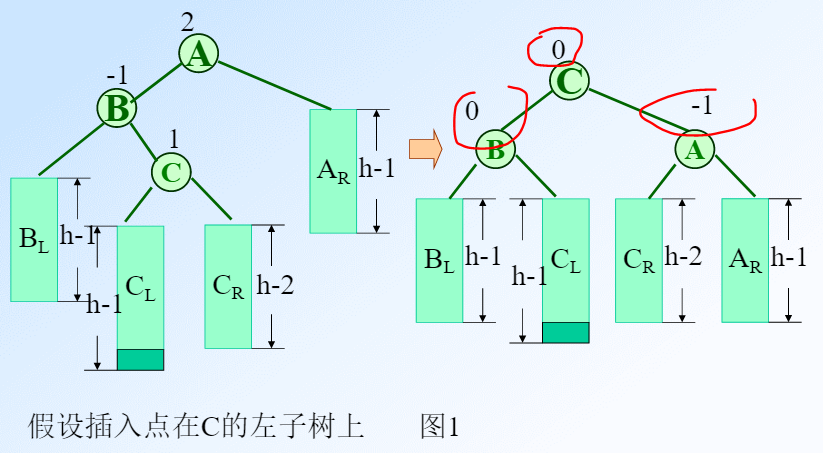
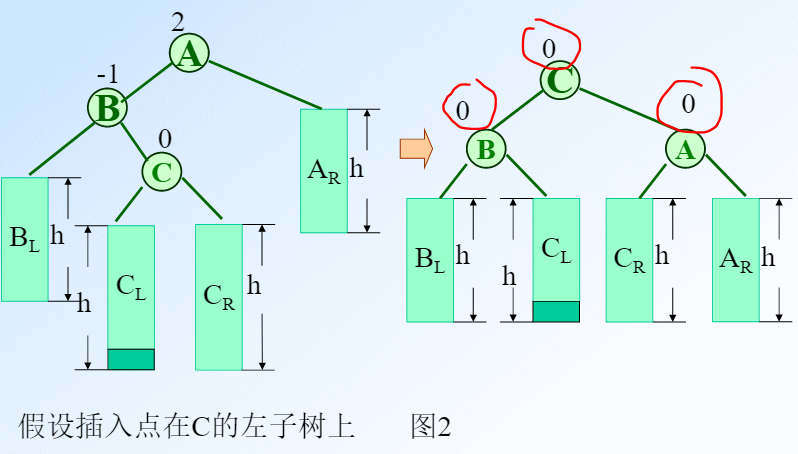
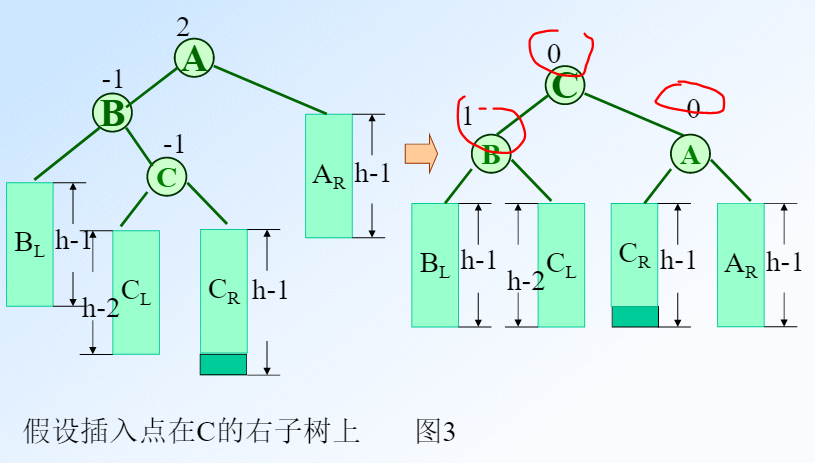
最后除此之外还要注意左右或右左的情况中旋转之后的bf值会不同。



可以通过c点来区分

B-树

一种多路平衡查找树

每个节点至多m个儿子，如果根节点不是叶子节点，那么最少2棵子树。根节点之外的非叶子节点都至少有 m/2个子树。

非终端节点包含n, A0, k1, A1, k1, A2…其中k是关键字，且k<k+1.n是关键字的数目

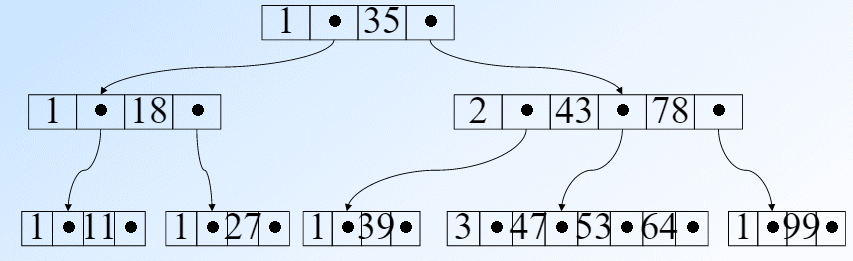
所有叶子节点都在同一层次且是空指针。

从上图中可以看出，对于每一个节点还是符合左边小右边大的规律的。

结构：

struct node
{
    int keynum;
    node *parent;
    int key[m+1];
    node *p[m+1];
    int *record[m+1];
}
struct result
{
    node *pt;
    int i;//节点中关键字序号
    int success;//是否找到
}

查找

result search(node *head, int key)
{
    node *p = head;
    mode *q;
    int found = 0;
    while(p && !found)
    {
        n = p->keynum;
        int i = search(p, key);//这个函数是找第一个大于等于key的
        if(i>=0 && p->key[i] == key)
        {
            found = 1;
        }
        else
        {
            q = p;
            p = p->p[i];
        }
    }
    if(found != 0)
    {
        result a.pt = p;
        a.i = i;
        a.success = 1;
    }
    else
    {
        result a.pt = q;//因为没找到最后一定会到null，所以返回它父亲
        a.i = i;
        a.success = 0;
    }
}

插入

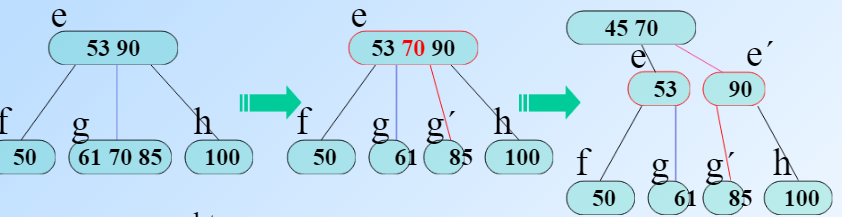
节点插入首先是查找，前面查找的时候已经返回了他应该在的位置。但是如果插入后超过了上限那么还要把中间节点提到上面去（主要讲三叉）。同时让左右两边的做往上提节点的左右两边。


上面是插入85

算法：

void insert(node *head, int key, node *in, int position)
{
    //in是要插入的节点，例如上面就是g节点
    //position是插入位置，也可以先用一次查找
    int x = key；
    node *ap = NULL;
    int finish = 0;
    while(q && !finish)
    {
        for(int k=position; k<in->keynum-1; k++)
        {
            in->key[k+1] = in->key[k];
        }
        for(int i=position+1; i<in->keynum; i++)
        {
            in->p[i+1] = in->p[i];
        }
        in->key[position] = x;
        in->keynum++;
        if(in->keynum < m)
        {
            finish = 1;
        }
        else
        {
            //要把数往上提
            int temp = (m%2==0) ? m/2 : m/2+1;
            x = in->key[temp];
            //分裂
            ap = in->parent;
            for(int i=0; i<ap->keynum-1; i++)
            {
                if(ap->key[i] < x)
                {
                    position = x;
                    break;
                }
            }//search
            for(int i=position+1; i<ap->keynum; i++)
            {
                ap->p[i+1] = ap->p[i];
            }
            node *left = new node;//拆分后左边节点
            node *right = new node;//拆封后右边节点
            //拆分具体过程就不写了，一系列的赋值
            ap->p[position] = left;
            ap->p[position+1] = right;
            in = ap;
        }
    }
    if(!finish)
    {
        head->keynum++;
        head->key[0] = key;
        //创建新结点
    }
}
这是自己写的并且没有验证，只有借鉴作用

删除

  • 如果删除这个值后节点的key数大于 m/2-1（此时分支数是m/2)。那么只需要删除对应部分，其他不变。
  • 如果删除节点后key=m/2-1
    1. 如果它父亲左边或者右边Key数大于m/2-1，那么先把左边最大（右边最小）提到上面，再把那个值放下来
    2. 如果左右两边正好都等于m/2-1，那么把左边右边合并并且把这个值也放下来
    3. 不会有小于m/2-1的了，不符合定义
  • 如果删除后双亲key值小于m/2-1,层层向上合并（不清楚具体过程）

B+树

b+树key和q一样多，并且子节点中包含父节点中的信息。

哈希表

基本思想：建立要存的数和存的位置之间的映射关系（最理想的情况是一一映射），此后在查找元素时，只需要用hash函数就可以找到再表中的位置。

哈希函数就是将值转化成存的位置的函数。

举个例子： 比如哈希函数是 x%10-1,那么可以输入x就可以得到元素在表中的位置。

但是这里有个问题，例如11的哈希值和1的哈希值相同，那么存的位置也相同，这显然是不允许的，这叫做哈希冲突。判断哈希函数优劣就是哈希冲突越少越好。

字符串哈希

直接定值法

hash(key) = key 或 hash(key) = a * key + b

这种方法仅适合哈希表和取值范围一样大的情况（如果取值到十亿我就呵呵）

数字分析法

这是利用所选数字中的一些规律来的。例如某一串数字最高若干位都相同，只有一两位不同，那么我们就可以只取一两位

平方取中法

就是先把数字平方然后再取中间几位，它的目的是扩大差别从而缩小冲突几率。适用于每一位都有高概率的重复数字。

折叠法

将关键字分成若干块然后叠加。可以直接分成若干块叠加。也可以正的加一块然后把数倒过来加一块，这种方法使用于位数多的情况。

除留余数法

hash(key) = key % p;//p是不大于表长且不大于最大值的素数

随机数法

hash(key) = random(key);//这是伪随机数

处理冲突的方法

开放地址法

把冲突的地址求一个地址序列：h0,h1…

h(i) = (h(key) + d(i) ) mod m // m是表长

d(i) = c + i c可以随便取

或d(i) = (-1)^(i-1) * (i/2)^2 //这里的i/2是向上取整也就是1/2=1

或d(i)=random(i)//伪随机数

或d(i) = i*h2(key)

注意，这里的d(i)要保证完备性，也就是要保证s(m-1)个h(i)均不相同并且要覆盖到所有地址。那么就要求

  1. 表长要是 4*k+3
  2. m与d(i)没有公因子

链地址法

把哈希值相同的记录在一个链表里。其实就是构建一个链表，如果不冲突就只有一个值，冲突就往后面加。

再哈希法

发生冲突时，选用另外一个哈希函数，直到不冲突。

建立公共溢出区

一旦发生冲突，就把有冲突的数据都填充到溢出表。

哈希表查找

就是先计算处hash(key)，如果找到直接填充，如果发现冲突就在通过冲突处理方法进行查找