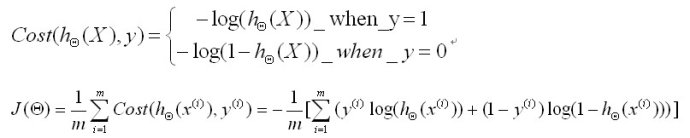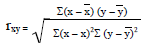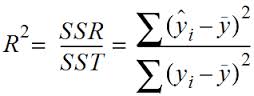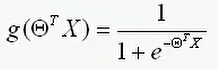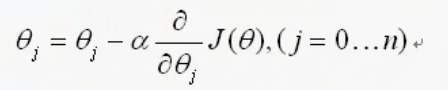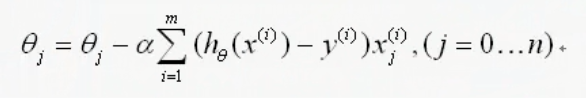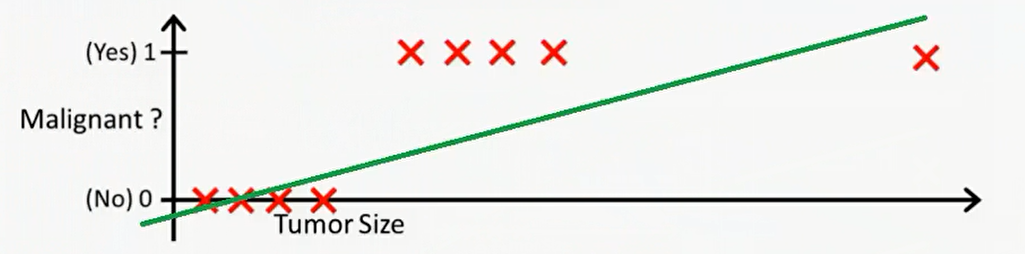
逻辑回归（logistic regression)

非线性回归例子：.这个例子中的关系不能很好的用线性关系进行模拟，所以我们要另外做曲线模拟它。

为了更好的处理，还需要用sigmoid函数平滑化。

sigmoid函数图像为

所以预测函数为：

我们要求解的问题可以转化成，求解一组参数使得J()最小化。求解方法时求偏导让导数为零。

当然上面这个方法求解过于复杂，我们也可以使用梯度下降的方法。非线性方程其实就是一个超平面，我们可以求偏导找出梯度，沿着梯度下降的方向不断走就可以找到最低点。

求解函数为

其中a是更新率（learning weight）

所以求完偏导的结果为：

h(x) = theta * x(i)

这就是更新函数，我们呢需要重复更新直到收敛

实例

import numpy as np
import random

def genData(numPoints,bias,variance):
# 产生实验数据，其中numpoint是实验个数，bias是偏差，variance是方差
    x = np.zeros(shape=(numPoints,2))
    y = np.zeros(shape=(numPoints))
    for i in range(0,numPoints):
        x[i][0]=1
        x[i][1]=i
        y[i]=(i+bias)+random.uniform(0,1)+variance
    return x,y

def gradientDescent(x,y,theta,alpha,m,numIterations):
# alpha是学习率 \ theta是我们要求的，开始可以随意赋值 \ m是实例个数 \ numIterations是重复次数
    xTran = np.transpose(x) # 转置，为了好算
    for i in range(numIterations):
        hypothesis = np.dot(x,theta) # dot是点积，算出h(x)。这个是一次全更新完
        loss = hypothesis-y
        cost = np.sum(loss**2)/(2*m) # 这个算法和上面讲的有所不同，相当于(h(x)-y(i)) * x(j)求和
        gradient=np.dot(xTran,loss)/m
        theta = theta-alpha*gradient
        print ("Iteration %d | cost :%f" %(i,cost))
    return theta

x,y = genData(100, 25, 10)
print "x:"
print x
print "y:"
print y

m,n = np.shape(x)
n_y = np.shape(y)

print("m:"+str(m)+" n:"+str(n)+" n_y:"+str(n_y))

numIterations = 100000
alpha = 0.0005
theta = np.ones(n)
theta= gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)