本文最后更新于 2024年10月1日 上午
最小生成树
如果图中有权值,称为网,仅在无向图中考虑这些问题,生成树指删去一些边变为树
kruskal算法
这个也被称为加边法,
- 把图中所有边按权值从小到大排序
- 把图中n个点看为n个独立的连通块
- 选择端点分属两个联通块且权值最小的边,若可选择的边有多条,任选其中一条即可
- 重复三,直至只剩一个连通块
如何存边?
1
2
3
4
5
6
7
8
| struct node
{
int u,v,w;
friend operator <(const node &x,const node& y)
{
return x.w<y.w;
}
}e[maxm];
|
其中u代表起点v代表终点,而w代表权值
采用了并查集的思想
怎么看加边后是否会变成环?只需要查找u,v的根节点,如果根节点相同则说明加边后 会变成环
模板,n个点m条边,找最小生成树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| #include<iostream>
#include<vector>
#define MAXN 1000
using namespace std;
struct node
{
int s,e,w;
friend opoerator < (const node& x,const node& y)
{
return x.w<y.w;
}
};
int father[100000];
int init(int n)
{
for(int i=1;i<=n;i++)
{
father[i]=i;
}
}
int find(int a)
{
int r=a;
while(father[r]!=r)
{
r=father[r];
}
int x=a;
while(father[x]!=x)
{
int j=father[x];
father[x]=x;
x=j;
}
return r;
}
void join(int x,int y)
{
int fx=find(x);
int fy=find(y);
if(fx!=fy)
{
father[fx]=fy;
return 1;
}
return 0;
}
int main()
{
int n;
while(cin>>n)
{
int m;
if(n==0)
{
break;
}
init();
cin>>m;
int ans=0;
vector<node> nod[m];
for(int i=0;i<m;i++)
{
cin>>nod[i].s>>nod[i].e>>nod[i].w;
}
sort(nod.begin(),nod.end(),cmp);
int k=0,i=0;
while(k<n-1)
{
if(join(nod[i].s,nod[i].e))
{
k++;
ans+=nod[i].val;
}
i++;
}
cout<<ans<<endl;
}
return 0;
}
|
prim 算法
先把点分为两个集合,在最开始的时候第一个集合中只有任意一点,其他点在另外一个集合中,之后选择属于集合一点在集合B中一点在集合A中且与A权值最小的边
选择时注意只要把最近选的那个点的权值与原来 权值相比就可以了
我们如何保存边?用邻接矩阵
在这里我们不用考虑形成环的问题,因为我们是从两个集合中拿边,而想要形成环必定是在一个集合内拿边
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| int g[maxn][maxn],dis[maxn];
bool mark[maxn];
long long prim()
{
memset(dis,ox3f,sizeof(dis));
memset(mark,0,sizeof(mark));
long long ans=0;
int u=1,mi;
mark[u]=true;
for(int i=1;i<n;i++)
{
for(int v=1;v<=n;v++)
{
dis[v]=min(dis[v],g[u][v]);
}
mi=ox3f;
for(int v=1;v<=n;v++)
{
if(!mark[v]&&dis[v]<mi)
{
u=v;
mi=dis[v];
}
}
ans+=mi;
mark[u]=true;
}
return ans;
}
|
注意,g数组开始要初始化为正无穷
最短路
在有向网中,求结点之间边权和最小的路被称为最短路问题
多源最短路
多源最短路指的是任意两点之间的最短路径
一般采用floyd-warshall算法,并且要求图中没有负权环(不然一直绕着环走就可以一直减小)
flord算法
用一个二维数组f[i][j]表示从i到j最小路长度,初始化时输入i,j点的路的长度并且f[i][i]=0.
我们怎么找到最短的路程呢? 通过观察可以发现,如果我们把一些点作为中转点的话,有可能会让路程变小。例如,我们只用1作为中转,可以得到
f[i][j]=min(f[i][j],f[i][1]+f[1][j]);
如果我们拿1和2作为中转点,可以得到
f[i][j]=min(f[i][j],f[i][1]+f[1][j]);
f[i][j]=min(f[i][j],f[i][2]+f[2][j]);
这段代码的意思是我先拿1作为中转,找到1做中转的最小路径之后我再拿2做为中转
模板

第一层是k,表示以1,2。。。n为中转
离散上的传递闭包

单源最短路
dijkstra
dijkstra只适用于无负权的图。
默认s可达全部点,用dis[i]表示从s到i的最短路径。
它的基本思想是贪心,将从单源单点最短路径化为单源多点最短路径。也就是计算从起始点出发到所有点的最短路径。
松弛操作
每次给目标集合加入一个点时,都要用该点重新判断最小的路径。
每次选择完一个点之后,这个点就由估计值变成确定值,也就是确定这个值就是从起点到这个点的最短路径(因为现在推到从起点到这个点是最短了,就算后面其他节点连接到这个节点也只会比这个路径更长)
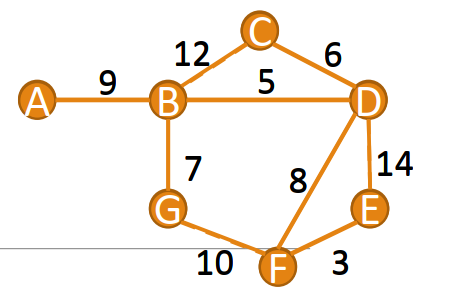
例如上面这个图,第一选择B,之后更新一遍之后选择D。虽然A->B->C->D这条路径,但是A->B->C就比A->B->D长了,之后就更不用说了。
每次进行松弛操作就是考虑加入这个点之后最短的点,这样每次都可以固定一次最短路径,进行n-1次就可以固定所有的最短路径。
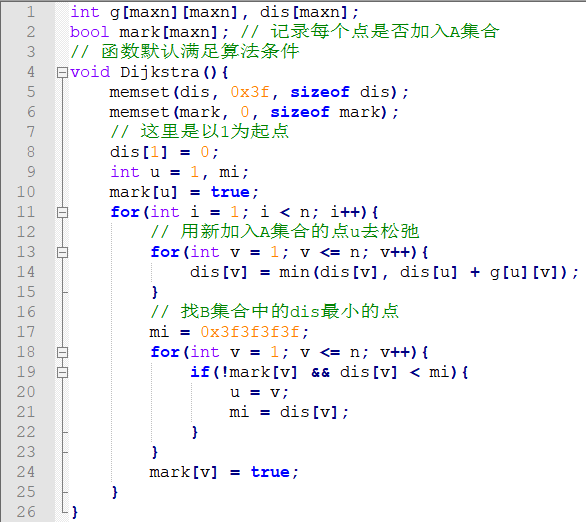
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
void dijkstra(int x)
{
int visit,i,j,min,next=x;
memset(visit,0,sizeof(visit));
for(i=1;i<=n;++i)
dis=map;
visit=1;
for(i=2;i<=n;++i)
{
min=INF;
for(j=1;j<=n;++j)
{
if(!visit&&dis<min)
{
min=dis;
next=j;
}
}
visit=1;
for(j=1;j<=n;++j)
{
if(!visit&&dis>dis+map)
dis=dis+map;
}
}
}
|
Bellman-Ford
该算法是通过每一条边进行降距操作(前面是通过点)。它的优点是可以有负权,并且可以检查出负权环。
过程:
- 进行初始化,将distance变成$+\infty$
- 用每一条边进行松弛操作
- 重复上述过程n-1次
为什么dijkstra不可以有负权图而下面可以?
- dijkstra是贪心选择,选中了就认为是最短路径,但是有可能发生到了之后原本路径长的通过一条负权结果路径比原来选择的那条还短的问题。
- Ford每次并没有进行选择,第一次松弛操作之后,因为访问了所有边,所以可以确定从起点找第一个点的最短路径。之后第二次又可以找到一个,依次进行。就算有负权因为每一次都是访问所有的边且并没有选择,所以负权也只会起到更新作用。
开始有一点疑惑时假设有负权那么每次经过负权的话长度不会变吗?其实如果dis[from]确定的话dis[from]+edge.weight也确定了下来,导致dis[to]经过一次松弛之后也确定了下来
1
2
3
4
5
6
7
8
9
| for (var i = 0; i < n - 1; i++) {
for (var j = 0; j < m; j++) {
var edge = edges[j];
if (distance[edge.to] > distance[edge.from] + edge.weight ){
distance[edge.to] = distance[edge.from] + edge.weight;
}
}
}
|
检查是否有负权环的方法:
- 再进行一次松弛操作,如果dis变化就有负权环(因为n-1次操作之后正常情况所有点的最短路径都是确定的)



